中学数学で学習する重要な公式たちをまとめておきます。
入試や学力テストなど
大きなテストの前には、こちらの記事で公式をチェックしておきましょう(^^)
計算
数学の計算問題に関する覚えておきたい技法、公式をまとめておきます。
ルートの有理化
分母にあるルートを消したいときには、分母と分子の両方に同じルートをかけてやりましょう。
詳しくはこちらの記事でも解説しています。
分母にルートがない形に変形しなさい。
$$\frac{6}{\sqrt{3}}$$
乗法公式
$$(x+a)(x+b)=x^2+(a+b)x+ab$$
$$(a+b)(a-b)=a^2-b^2$$
$$(a+b)^2=a^2+2ab+b^2$$
$$(a-b)^2=a^2-2ab+b^2$$
乗法公式の詳しい使い方はこちらで解説しています。
次の式を展開しなさい。
$$(x+2)(x-4)$$
$$(x+3)(x-3)$$
$$(x+3)^2$$
$$(x-6)^2$$
方程式
方程式を解くために覚えておきたい公式です。
解の公式
二次方程式\(ax^2+bx+c=0\)の解は
$$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$$
二次方程式の解き方についてはこちらの記事で解説しています。
次の二次方程式を解きなさい。
$$x^2+3x+1=0$$
関数
関数において覚えておきたい公式をまとめておきます。
関数の式
【比例】 \(y=ax\)
【反比例】 \(\displaystyle{y=\frac{a}{x}}\)
【一次関数】 \(y=ax+b\)
【\(y\)は\(x\)の二乗に比例する関数】 \(y=ax^2\)
関数の式の作り方についてはこちらの記事で解説しています。
次のとき、関数の式を作りなさい。
\(y\)は\(x\)に比例し、\(x=2\)のとき\(y=6\)になる。
\(y\)は\(x\)に反比例し、\(x=-2\)のとき\(y=3\)になる。
\(y\)は\(x\)の二乗に比例し、\(x=3\)のとき\(y=18\)になる。
変化の割合
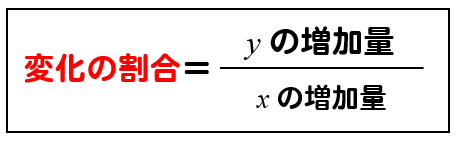
変化の割合は上のような式で求めることができます。
ですが、これにプラスして覚えておきたいことがあります。
一次関数の変化の割合は傾きと等しい。

\(y=ax^2\)の変化の割合は裏ワザ公式あって
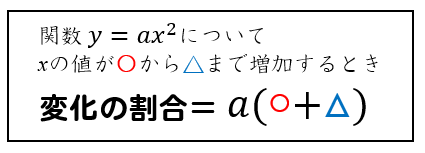
このように求めることができましたね。
詳しくはこちらの記事で解説しています。
>【変化の割合】簡単な求め方は?一次関数、二乗に比例する関数のやり方
次の\(x\)の値が2から4まで増加するとき、次の関数の変化の割合を求めなさい。
$$y=-3x+4$$
$$y=2x^2$$
図形
図形における様々な公式をまとめておきます。
円、おうぎ形
円の公式
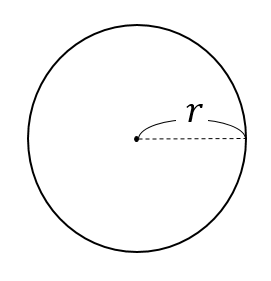
円の面積: \(\pi r^2\)
円周の長さ: \(2\pi r\)
おうぎ形の公式
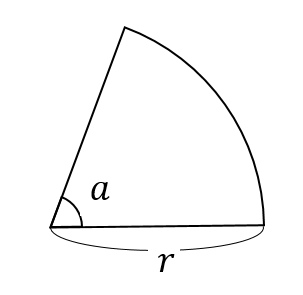
おうぎ形の面積: \(\displaystyle{\pi r^2\times \frac{a}{360}}\)
おうぎ形の弧の長さ: \(\displaystyle{2\pi r\times \frac{a}{360}}\)
詳しくはこちらの記事でも解説しています。
半径3㎝の円周の長さ、面積
半径3㎝、中心角60°のおうぎ形の弧の長さ、面積
体積
柱体
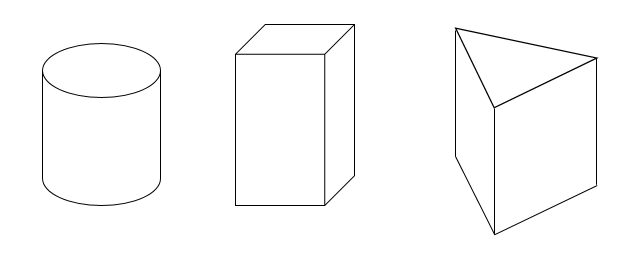
$$(体積)=(底面積)\times (高さ)$$
錐体
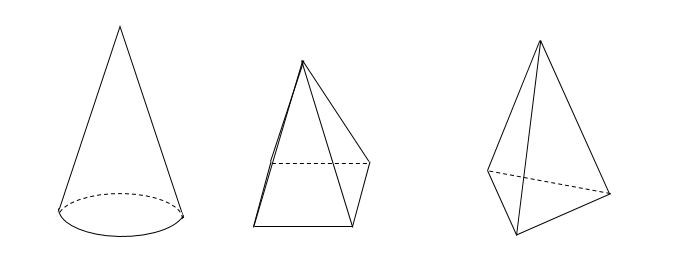
$$(体積)=(底面積)\times (高さ)\times \frac{1}{3}$$
次の立体の体積を求めなさい。
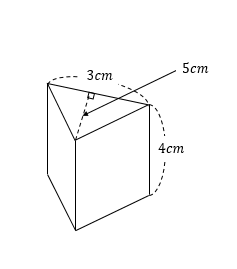
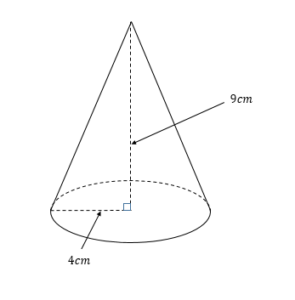
円錐の中心角、表面積
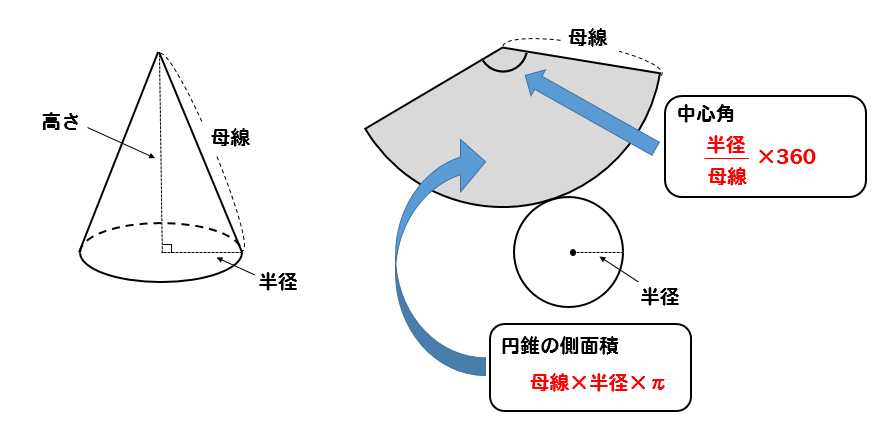
詳しくは、こちらの記事で解説しています。
次の円錐の表面積を求めなさい。
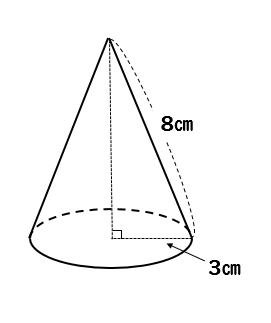
球
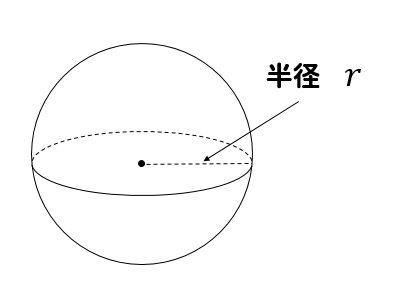
球の表面積: \(\displaystyle{4\pi r^2}\)
球の体積: \(\displaystyle{\frac{4}{3}\pi r^3}\)
半径が3㎝である球の表面積、体積を求めなさい。
合同条件
三角形の合同条件
- 3組の辺がそれぞれ等しい
- 2組の辺とその間の角がそれぞれ等しい
- 1組の辺とその両端の角がそれぞれ等しい
直角三角形の合同条件
- 直角三角形の斜辺と他の一辺がそれぞれ等しい
- 直角三角形の斜辺と1つの鋭角がそれぞれ等しい
>【直角三角形】証明問題の書き方とは?合同条件の使い方を徹底解説!
二等辺三角形
二等辺三角形の定義…2辺が等しい三角形
二等辺三角形の性質
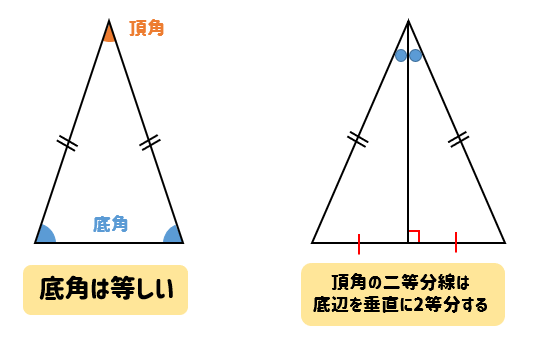
二等辺三角形になるための条件
- 2辺が等しい
- 2つの角が等しい
正三角形
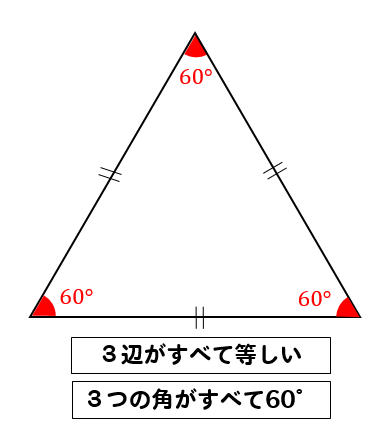
正三角形の定義…3辺が等しい三角形
正三角形の性質
- 3つの内角が等しい(すべて60°)
平行四辺形
平行四辺形の定義…2組の対辺がそれぞれ平行な四角形
平行四辺形の性質
- 2組の対辺がそれぞれ等しい
- 2組の対角がそれぞれ等しい
- 対角線はそれぞれの中点で交わる
平行四辺形になるための条件
- 2組の対辺がそれぞれ平行である
- 2組の対辺がそれぞれ等しい
- 2組の対角がそれぞれ等しい
- 対角線がそれぞれの中点で交わる
- 1組の対辺が平行でその長さが等しい
特殊な平行四辺形の定義
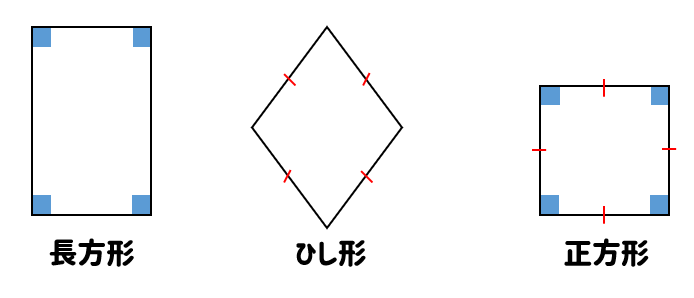
長方形の定義…4つの角がすべて直角である四角形
ひし形の定義…4つの辺がすべて等しい四角形
正方形の定義…4つの角がすべて直角で、4つの辺がすべて等しい四角形
相似条件
三角形の相似条件
- 3組の辺の比がすべて等しい
- 2組の辺の比とその間の角がそれぞれ等しい
- 2組の角がそれぞれ等しい
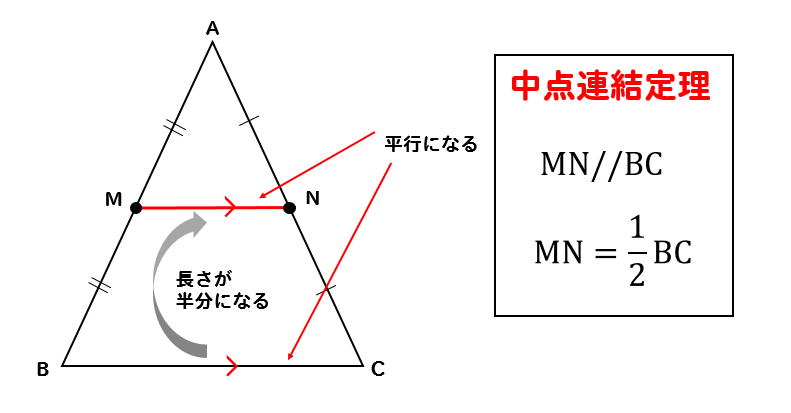
中点連結定理
△ABCにおいて、中点同士を結ぶと中点連結定理が成り立ちます。
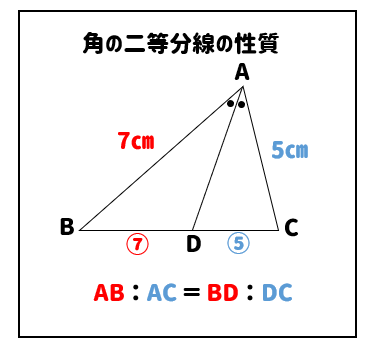
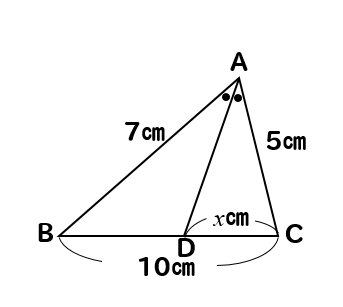
角の二等分線
>平行線と比の利用、辺の長さを求める方法をまとめて問題解説!
次の図形において、\(x\)の値を求めなさい。
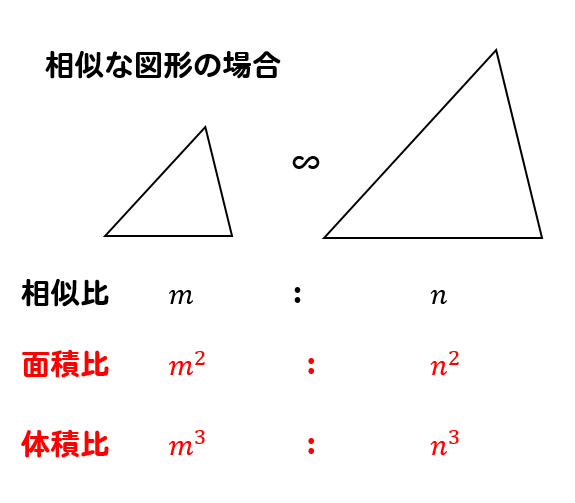
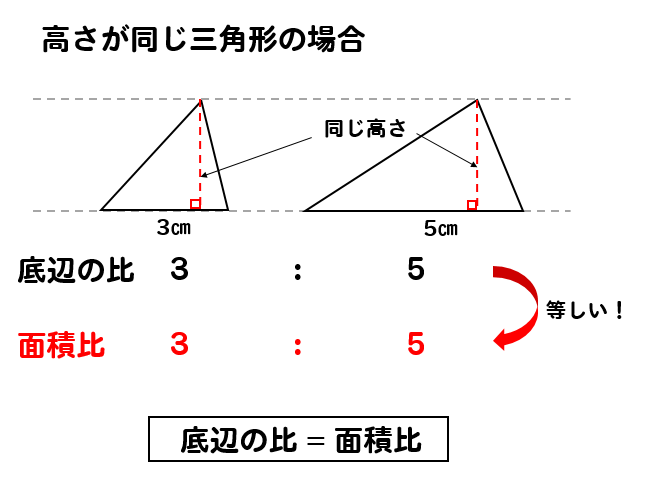
面積比、体積比
円周角の定理
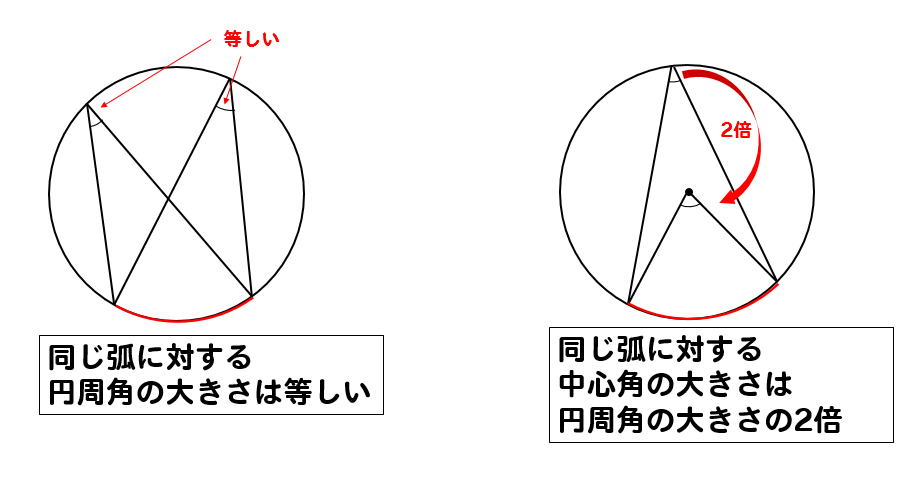
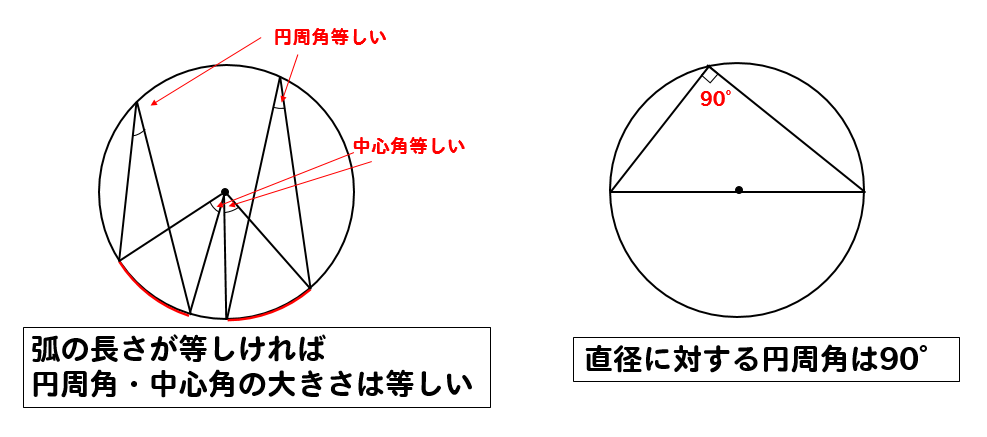
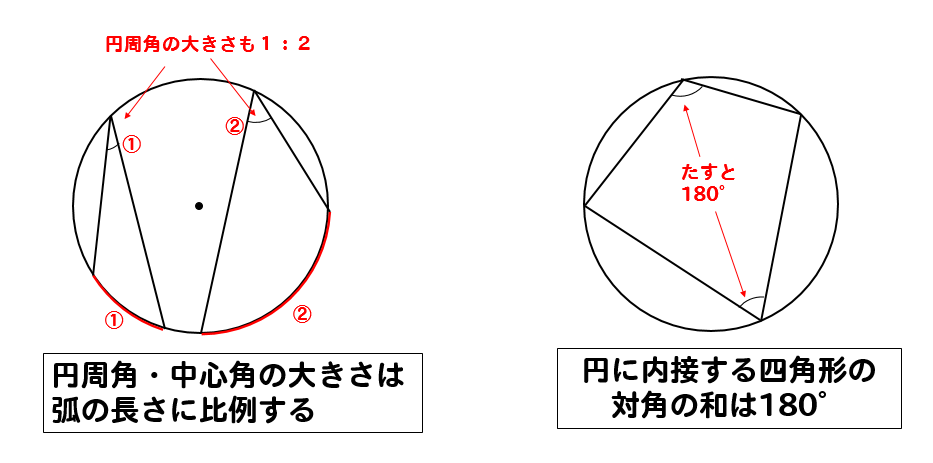
円周角のパターン別問題円周はこちら
接弦定理
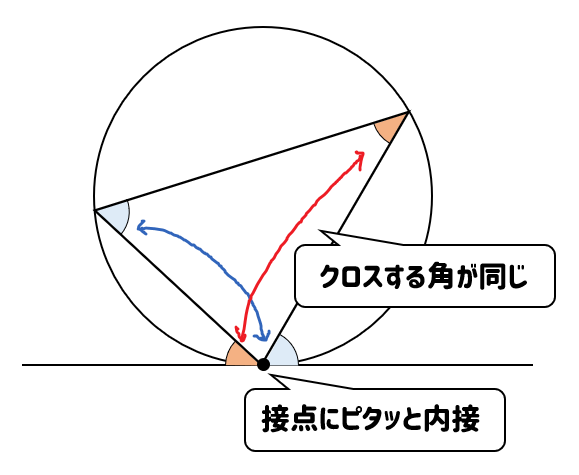
>【接線と弦のつくる角の定理】問題の解き方、証明をサクッと解説!
三平方の定理
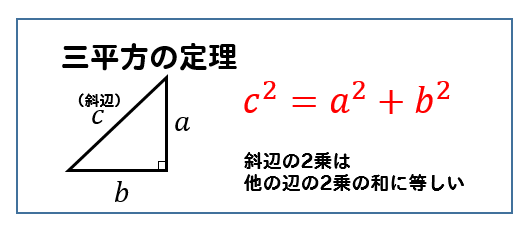
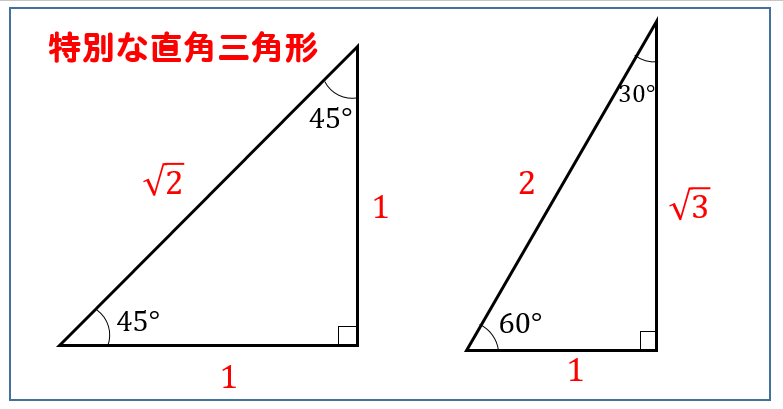
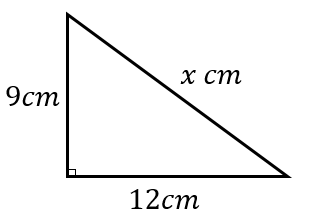
次の図形において、\(x\)の値を求めなさい。
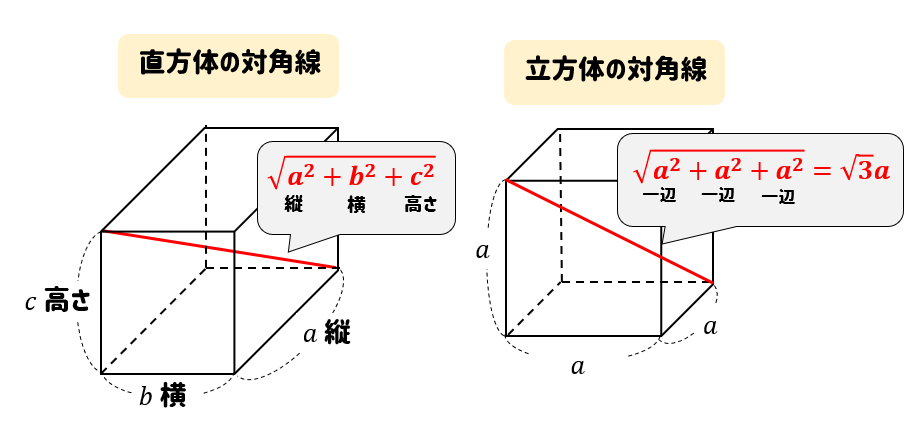
>直方体、立方体の対角線の長さは公式でラクラク計算できるぞ!
次の直方体の対角線の長さを求めなさい。
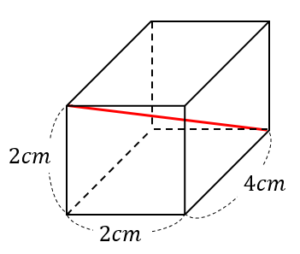
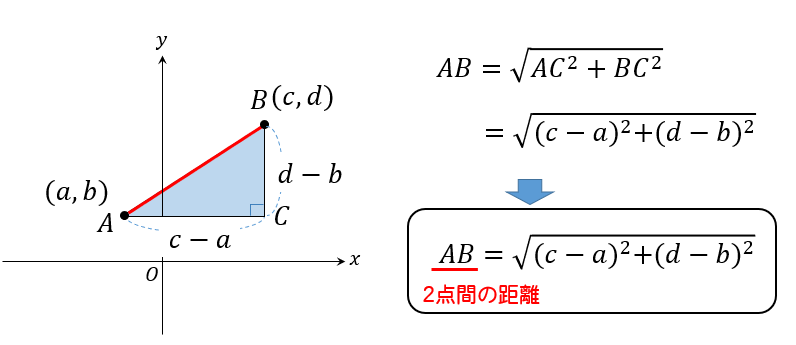
次の2点AB間の距離を求めなさい。
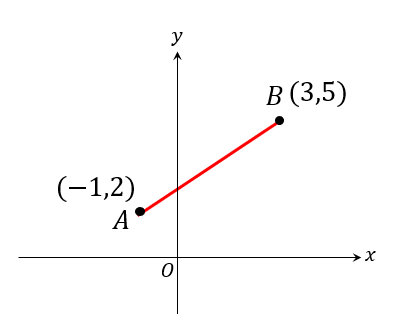
重要公式は以上!
みなさんの健闘を祈る!
テスト頑張れ(/・ω・)/

















相似条件の所間違っています。
正しくは、「3組の辺の比が全て等しい」です。
訂正お願い致します。
いいね
訂正しました。
ご指摘ありがとうございました!
角の二等分線の性質AB:ACです
訂正いたしました(^^;)
ご指摘ありがとうございました!
非常にわかりやすいです
ありがとうございます!!
イイね!
参考になったようで嬉しいです!
コメントありがとう(/・ω・)/
受験勉強の参考にさせて頂きました。
分かりやすかったです。
ありがとうございます❊
あざっす
ありがとうございます(^^)
受験勉強がんばってください!
平行四辺形や二等辺三角形の性質(二等辺三角形で底角は等しい や、 平行四辺形
で1組の辺が平行で等しい)も加わったらなお良いと思いました
ご指摘いただいた箇所を追加しておきました!
わかりやすいです(^^)
ありがとうございます!
ありがとうございます(/・ω・)/
めちゃくちゃ分かりやすくてありがたいです!
参考にさせていただきます(˶ ̇ ̵ ̇˶ )
ありがとうございます(^^)
勉強がんばってくださいね(/・ω・)/
すごく分かりやすいです残り1日なんで頑張ります
頑張ってください(/・ω・)/
接弦定理も加えて欲しいです
加えました!
わかりやすくて助かります
参考にしてくれてありがとう!!
分かりやすい~ まとまっているのはいいですね
ありがとうございます!
ぜひ参考にしてみてくださいね(^^)
すごいためになりましたぁぁ!!!ほんとにありがとうございます( இ﹏இ )みんなのためにこれを作る主さんいい人すぎる(⸝⸝⸝ᵒ̴̶̷̥́ ⌑ ᵒ̴̶̷̣̥̀⸝⸝⸝)
そういっていただけると作った甲斐があります。
ありがとうございます(^^)
とても参考になりました。
ありがとうございました
ありがとうございます!!
明日本番です!前日の確認としてとてもありがたかったです。ありがとうございます!!
受験お疲れさまでした!
良い結果であることを願っています。
いつもお世話になっております。 先生の教え方は学校の先生と違った教え方でとても分かりやすいです(^-^)これからもよろしくお願いします✨
体調に気をつけてください!
ありがとうございます!
そういってもらえると
頑張って解説記事を書いて良かったです^^
受験勉強の参考にさせていただきました!
凄く分かりやすかったです!良かったです!!
作ってくれてありがとうございます(*⌒▽⌒*)
体調をくずされませんようお元気でお過ごしください
嬉しいお言葉ありがとうございます^^
高校生になっても学びは続いていきます。
これからもぜひ数スタをご活用くださいね!
お互い元気でいきましょー!
わかりやすい。
ありがとうございます!!
とてもわかりやすいです!!
参考にさせてもらいます。
ありがとうございます!
出やすいポイントをまとめたので
テスト前にチェックしてもらえると嬉しいです^^
いいね
ありがとうございます!!
すごくわかりやすかったです!!方べきの定理についての情報も追加してくれたらうれしいです!これからも頑張ってください!!
ありがとうございます!
方べきの定理も加えておこうかな!!
分かりやすかった。
ありがとうございます^^
めちゃくちゃ分かりやすくて助かったし、ありがたい!!
ありがとうございます!!
ばり分かりやすい。
ありがとうございます!!
分かりやすくて、スゴくいいです!!
ありがとうございます!!
あしたてすとだけど見てよかった
明日が入試かな?
健闘を祈ります!
がんばってね(^^)v
分かりやすいです‼
ありがとう!
すごくわかりやすくて理解できてなかったところがスッと頭に入ってきました!
応用問題にも対応できるようにがんばります!
応用もがんばってください(‘ω’)ノ
分かりやすかったです。
明日の受験がんばります。
ファイトです!!!!
すごくわかりやすくて勉強になりました!
ありがとうございます。
これからも頑張ってください!
ありがとうございます!
僕もがんばります!!
とてもわかりやすく受験勉強の参考にさせていただきました!!ありがとうございます!
受験勉強のお役に立てて良かったです!
基礎はバッチリ満点をとってきてくださいね^^
すごく分かりやすくとても参考になりました!
うろ覚えのところがあったのでここで確認できて良かったです。
ありがとうございます
お役に立てて良かったです!
入試で力が発揮できることを願ってます!
ホンマにためになりました!
ありがとうございます
明日私立受験なので、これみて公式確認できてちょっと安心出来ました!
試験お疲れ様でした!
満足いく結果になることを願ってます!
願いよ届けーー(/・ω・)/
分かりやすく説明など書いてくれてありがたいです!
1人でするのに理解があまり出来ないものもあったのでこのようにまとめてくださって凄く嬉しいです(*´꒳`*)
約1週間後入試なので頑張ります!!!
いよいよですね!
全力を出し切れるように願ってます^^
ファイト、ファイト、ファイトだ(/・ω・)/
わかりやすくて助かります!
受験頑張ります!
ありがとうございます^^
受験ファイトです(/・ω・)/
ありがとう
お役に立てて良かったです^^
明日受験です!円のクロスする角一緒なの知りませんでした!ありがとうございます!
お役に立てて良かったです^^
受験が上手くいっているとイイなぁ~!
めっっっっちゃ参考になりました!
お役に立てて嬉しいですっ!!!
受験まで頑張って覚えます‼︎ ありがとうございます
はい!がんばってください^^
応援しています(‘ω’)ノ
めちゃくちゃ助かりました……❕
愛用してます……❣️
ありがとうございます^^
これって中学一年生から3年生までをまとめたものですか?
そのつもりです!
受験を間近に控えていて公式が不安になっている部分がいくつかあったので、とても助かりました!!!おかげで頑張れそうです!ありがとうございますm(_ _)m
応援してます!
めちゃくちゃ役に立ちました!
ありがとうございます。
接頭三角柱や切頭四角柱、切頭円柱等の体積公式加えればよりためになると思います!
めちゃくちゃわかりやすかったです
分かりやすかったです!
分かりやすかったです!
神すぎこれ、お前最高!
とてもわかりやすかったです!
とてもわかりやすいです”
こういうのめちゃめちゃ助かります!
入試直前で覚えてないことが多く、覚えられるか心配でしたが非常に分かりやすくすぐに覚えられました。本当にありがとうございます。
受験のために見ました
分かりやすいとは思いましたでも理解するのに時間かかりそうです…w