今回は中1で学習する
『平面図形』の単元から
おうぎ形の公式について、まとめて解説していくよ!
問題演習もつけているので
問題に挑戦しながら公式を身につけていこう!
覚えておきたい円、おうぎ形の公式
おうぎ形の公式を学習するためには
まず円の公式を覚えておく必要があります。
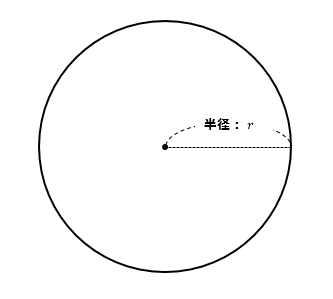
円の面積、円周の長さの公式
円の公式

円周の長さ
$$2\pi r$$
円の面積
$$\pi r^2$$
演習問題で理解を深める!
(1)解説&答えはこちら
答え
円周の長さ:\(6\pi cm\)
面積:\(9\pi cm^2\)
円周の長さを求めるためには\(2\pi r\)の公式にあてはめます。
$$2\pi \times3=6\pi cm$$
円の面積を求めるためには\(\pi r^2\)の公式にあてはめます。
$$\pi \times 3^2=9\pi cm^2$$
(2)解説&答えはこちら
答え
円周の長さ:\(16\pi cm\)
面積:\(64\pi cm^2\)
円周の長さを求めるためには\(2\pi r\)の公式にあてはめます。
$$2\pi \times8=16\pi cm$$
円の面積を求めるためには\(\pi r^2\)の公式にあてはめます。
$$\pi \times 8^2=64\pi cm^2$$
(3)半径が10㎝の円周の長さと面積を求めなさい。
(3)解説&答えはこちら
答え
円周の長さ:\(20\pi cm\)
面積:\(100\pi cm^2\)
円周の長さを求めるためには\(2\pi r\)の公式にあてはめます。
$$2\pi \times10=20\pi cm$$
円の面積を求めるためには\(\pi r^2\)の公式にあてはめます。
$$\pi \times 10^2=100\pi cm^2$$
円の公式が身についたら
次はおうぎ形の公式を確認していきましょう!
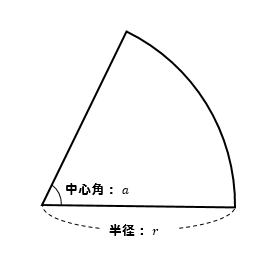
おうぎ形の弧の長さ、面積の公式

おうぎ形の弧の長さ
$$2\pi r \times \frac{a}{360}$$
おうぎ形の面積
$$\pi r^2 \times \frac{a}{360}$$
円の公式を覚えていれば
おうぎ形の公式は\(\times \frac{a}{360}\)をくっつけるだけで作ることができますね!

演習問題で理解を深める!
(1)半径6㎝、中心角120°のおうぎ形の弧の長さと面積を求めなさい。
(1)解説&答えはこちら
答え
弧の長さ:\(4\pi cm\)
面積:\(12\pi cm^2\)
弧の長さを求めるためには\(2\pi r \times \frac{a}{360}\)の公式にあてはめます。
$$2\pi \times 6 \times \frac{120}{360}$$
$$=12\pi \times \frac{1}{3}$$
$$=4\pi cm$$
円の面積を求めるためには\(\pi r^2 \times \frac{a}{360}\)の公式にあてはめます。
$$\pi \times 6^2 \times \frac{120}{360}$$
$$=36\pi \times \frac{1}{3}$$
$$=12\pi cm^2$$
(2)半径4㎝、中心角45°のおうぎ形の弧の長さと面積を求めなさい。
(2)解説&答えはこちら
答え
弧の長さ:\(\pi cm\)
面積:\(2\pi cm^2\)
弧の長さを求めるためには\(2\pi r \times \frac{a}{360}\)の公式にあてはめます。
$$2\pi \times 4 \times \frac{45}{360}$$
$$=8\pi \times \frac{1}{8}$$
$$=\pi cm$$
円の面積を求めるためには\(\pi r^2 \times \frac{a}{360}\)の公式にあてはめます。
$$\pi \times 4^2 \times \frac{45}{360}$$
$$=16\pi \times \frac{1}{8}$$
$$=2\pi cm^2$$
(3)半径8㎝、中心角90°のおうぎ形の弧の長さと面積を求めなさい。
(3)解説&答えはこちら
答え
弧の長さ:\(4\pi cm\)
面積:\(16\pi cm^2\)
弧の長さを求めるためには\(2\pi r \times \frac{a}{360}\)の公式にあてはめます。
$$2\pi \times 8 \times \frac{90}{360}$$
$$=16\pi \times \frac{1}{4}$$
$$=4\pi cm$$
円の面積を求めるためには\(\pi r^2 \times \frac{a}{360}\)の公式にあてはめます。
$$\pi \times 8^2 \times \frac{90}{360}$$
$$=64\pi \times \frac{1}{4}$$
$$=16\pi cm^2$$

おうぎ形の中心角の求め方
おうぎ形の公式を身につけたところで
次は発展問題の『中心角を求める』について解説していきます。
おうぎ形の中心角を求める方法は他にもあるんだけど
今回は、一番簡単そうなやつを紹介しておくね。
他の方法については、こちらの記事を参考にしてください!
公式を見ただけでは、ちょっとわかりにくいから
例題を使って解説していくね!
例題
半径\(6\)㎝、弧の長さ\(8\pi\)cmのおうぎ形の中心角を求めなさい。
おうぎ形の弧の長さが与えられているので

こちらの公式を利用します。
まずは、半径6㎝の円の円周の長さを求めます。
$$2\pi \times 6=12\pi cm$$
そして、公式にそれぞれの値をあてはめていくと
$$\frac{8\pi}{12\pi}\times 360$$
約分をしていきましょう。
(πも約分で消えてしまいます)
$$=\frac{2}{3}\times 360$$
$$=240°$$
このように公式に当てはめていけば
簡単に中心角を求めることができます(^^)
それでは、演習問題で理解を深めていきましょう!
演習問題で理解を深めよう!
(1)半径\(9\)㎝、面積\(9\pi\)cm²のおうぎ形の中心角を求めなさい。
(1)解説&答えはこちら
おうぎ形の面積が与えられているので

こちらの公式を利用します。
まずは、半径9㎝の円の面積を求めます。
$$\pi \times 9^2=81\pi cm^2$$
そして、公式にそれぞれの値をあてはめていくと
$$\frac{9\pi}{81\pi}\times 360$$
約分をしていきましょう。
(πも約分で消えてしまいます)
$$=\frac{1}{9}\times 360$$
$$=40°$$
(2)半径\(12\)㎝、弧の長さ\(3\pi\)cmのおうぎ形の中心角を求めなさい。
(2)解説&答えはこちら
おうぎ形の弧の長さが与えられているので

こちらの公式を利用します。
まずは、半径12㎝の円の円周の長さを求めます。
$$2\pi \times 12=24\pi cm2$$
そして、公式にそれぞれの値をあてはめていくと
$$\frac{3\pi}{24\pi}\times 360$$
約分をしていきましょう。
(πも約分で消えてしまいます)
$$=\frac{1}{8}\times 360$$
$$=45°$$
円とおうぎ形の公式 まとめ
お疲れ様でした!
円とおうぎ形の公式を覚えれましたか??
公式がなかなか覚えれないという人の中には
円とおうぎ形の公式を別々に考えている人が多いです。
おうぎ形の公式は
円の公式に\(\times \frac{a}{360}\)をくっつけるだけですからね!
円の公式を覚えてしまえば
おうぎ形は、ついでに覚えちゃうことができるはずです。
おうぎ形の問題では、どうしても分数の計算が必要になってくるので
分数の計算が苦手な人は特訓しておく必要がありますね。
覚えるのが苦手だな…という人は
たくさん問題演習して、とにかく手を動かすことが大事!
ファイトだー(/・ω・)/

























解説など、とっても分かりやすく、自分自身あまり理解できてなかった部分も、結構理解できた気がします!
分かりやすかったです
良く理解できました。
お役に立てて良かったです!
おうぎ形はテストにも出やすいので
点数アップにつながることを願ってます^^
とても分かりやすく、頭の中にスルスルと入ってきました!
とても分かりやすかったです
学校では、よく分からないところがあったけどこのサイトで分かって良かったです!
お役に立てて嬉しいです!
公式は忘れやすいので、定期的にこのページで復習してくださいね^^
分かりやすかったです