【比例 反比例の式】式の作り方、違いは？問題を使って解説するぞ！

比例と反比例の式は、それぞれどのような形になっているのか。

どのように式を作ればよいのか。

ということについて解説していきます。

取り上げる問題は次の通りです。

【比例 反比例の式】式の作り方、違いは？

まずは、比例と反比例の式の形を覚えておきましょう。

それぞれこのような形になります。

あわせて、反比例については

$$xy=a$$

になるということも覚えておくと便利です(^^)

【比例の式】式の作り方は？

比例の式 \(y=ax\)に\(x=3\)、\(y=6\)を代入します。

$$\begin{eqnarray} 6&=&3a\\2&=&a\end{eqnarray}$$

よって、比例の式は

$$\color{red}{y=2x}$$

となります。

比例の式を作りたければ、\(y=ax\)の形を覚えておいて、そこに\(x,  y\)の値を代入するだけでOKですね。

【比例の式】グラフから式を作る

次の関数の式を作りなさい。

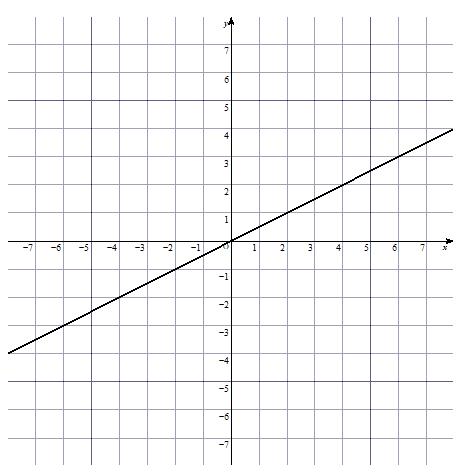
グラフから式を作りたい場合、グラフが通っている座標をどこでもいいので１つ読み取りましょう。

例えば

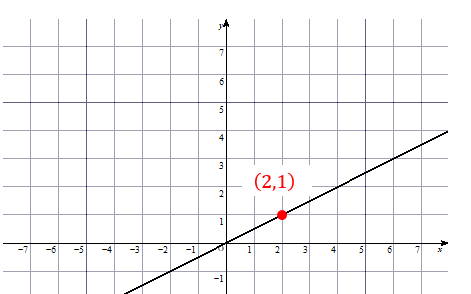
こんな感じで座標を１つ読み取ることができますね。

グラフが \((2, 1)\) を通るということは、\(x=2\)のとき、\(y=1\)になるということです。

このように考えると、さっきの問題と同じように式を作っていくことができますね。

比例の式 \(y=ax\)に\(x=2\)、\(y=1\)を代入します。

$$\begin{eqnarray} 1&=&2a\\\frac{1}{2}&=&a\end{eqnarray}$$

よって、比例の式は

$$\color{red}{y=\frac{1}{2}x}$$

となります。

グラフから式を作りたい場合には、まず座標を読み取る！

というのがポイントですね(^^)

【反比例の式】式の作り方は？

反比例の式 \(\displaystyle{y=\frac{a}{x}}\) に\(x=2\)、\(y=8\)を代入します。

$$\begin{eqnarray} 8&=&\frac{a}{2}\\8\times 2&=&\frac{a}{2}\times 2\\16&=&a\end{eqnarray}$$

よって、反比例の式は

$$\color{red}{y=\frac{16}{x}}$$

となります。

ただし、反比例の比例定数は、\(xy=a\)で求めることができることを覚えておけばラクに計算できます。

\(x=2\)、\(y=8\)だから

$$a=2\times 8=16$$

よって、反比例の式は

$$y=\frac{16}{x}$$

\(x\)と\(y\)の値を掛けるだけ！

反比例の式は楽勝ですね(^^)

【反比例の式】グラフから式を作る

次の関数の式を作りなさい。

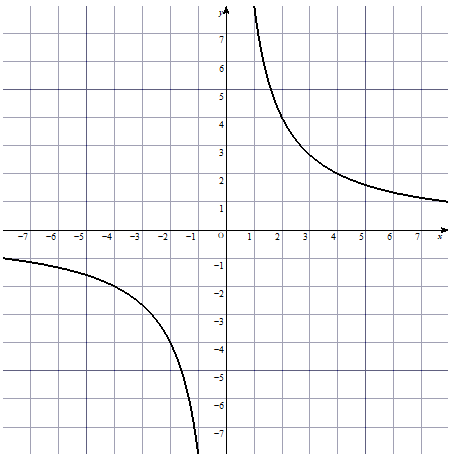
まずは、反比例のグラフが通る座標を１つ読み取りましょう。

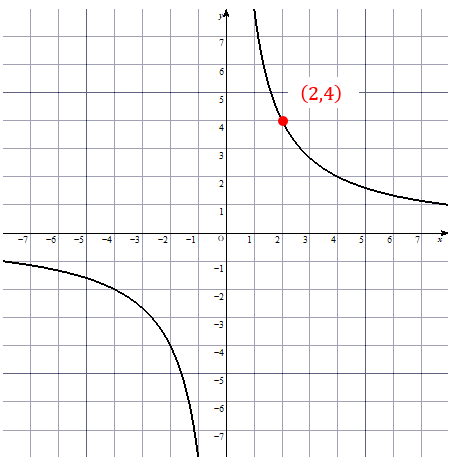
すると、このように\((2,4)\) という座標が読み取れます。

これは\(x=2\)のとき、\(y=4\)になるということだから

反比例の式 \(\displaystyle{y=\frac{a}{x}}\)に \(x=2\) と \(y=4\)を代入します。

$$\begin{eqnarray} 4&=&\frac{a}{2}\\4\times 2&=&\frac{a}{2}\times 2\\8&=&a\end{eqnarray}$$

よって、反比例の式は

$$\color{red}{y=\frac{8}{x}}$$

となります。

また、\(xy=a\) となることを覚えておけば

$$a=2\times 4=8$$

よって、反比例の式は

$$y=\frac{8}{x}$$

このように求めることができます。

グラフから座標を読み取る。

反比例の式\(\displaystyle{y=\frac{a}{x}}\)に代入するだけ！

楽勝ですね(^^)

【比例 反比例の式】式の作り方まとめ！

お疲れ様でした！

比例、反比例は、それぞれの式の形を覚えておけば楽勝ですね(^^)

たくさん問題を解いて、理解を深めていきましょう(/・ω・)/