【直角三角形の合同条件】証明問題の書き方とは？イチから徹底解説！

今回は中2で学習する図形の単元から

直角三角形の合同条件、証明問題について解説していくよ！

 

今回取り上げるテーマはこちら

証明問題の書き方を基礎から見直したい方は、まずこちらの記事を読んでみてくださいね(^^)

合同な三角形の証明問題の書き方を基礎から解説！

 

それでは、順に解説していきます。

 

直角三角形の合同条件、証明についてはこちらの動画でも解説しているのでご参考ください＾＾

 

 

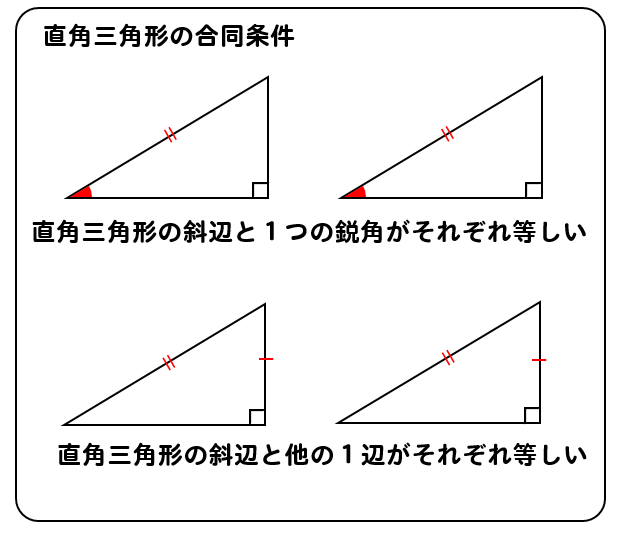
直角三角形の合同条件とは

直角三角形は、以下のことが分かれば合同だと言えます。

 

 

今までの三角形の合同条件が

 

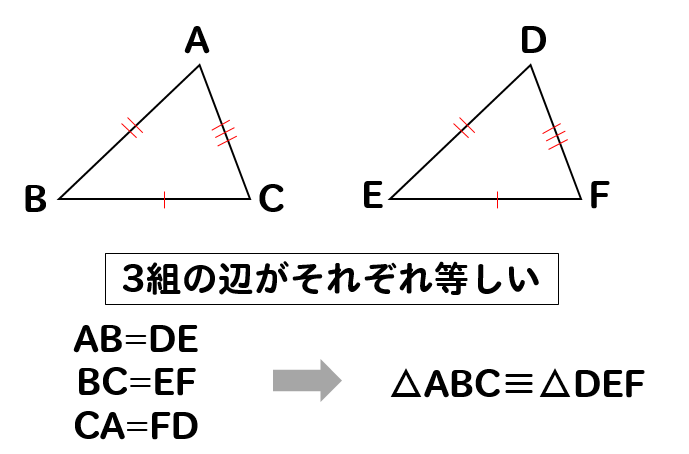
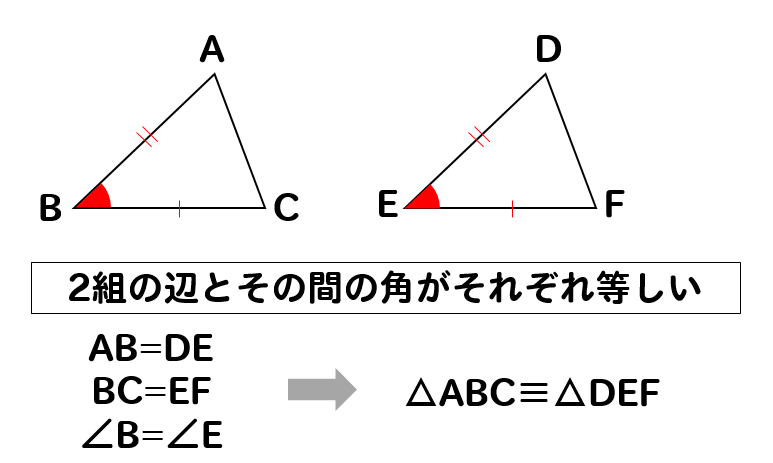
このように、3つの情報を組み合わせて合同を言うことができましたが

直角三角形の場合には

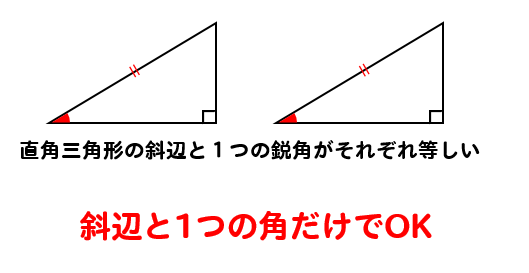
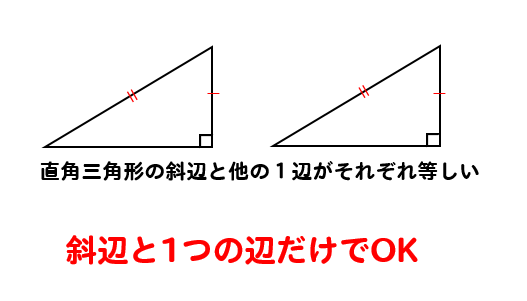
このように2つの情報だけでOKになります。

ちょっと便利ですね(^^)

 

 

ただし、直角三角形の斜辺が等しいことが前提となっているので注意ですね。

 

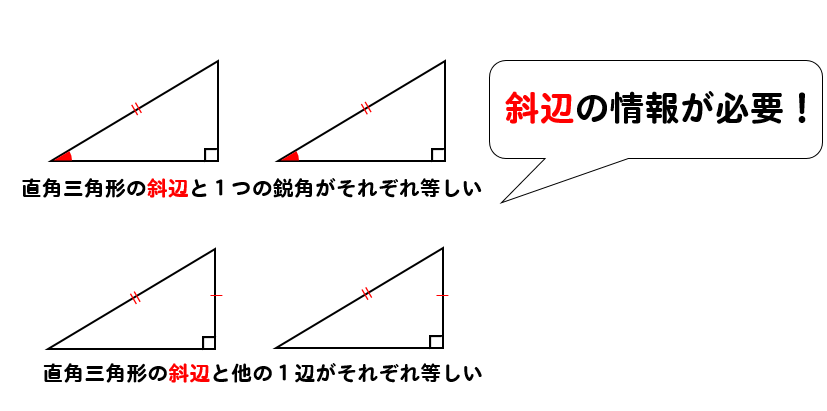
直角三角形の合同条件の理由は？

でも、なんで直角三角形の場合

2つの情報だけで合同が言えるんだろう？

 

『直角三角形の斜辺と１つの鋭角がそれぞれ等しい』から考えていきましょう。

 

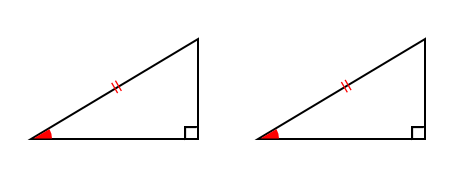
２つの角の大きさが等しいのだから、残り１つも同じ大きさになるはずだよね。

 

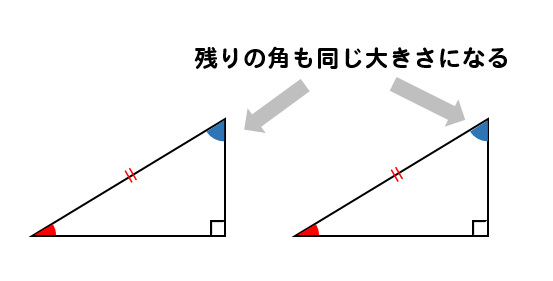
ということは、斜辺部分に注目してみると

１組の辺とその両端の角がそれぞれ等しくなりますね。

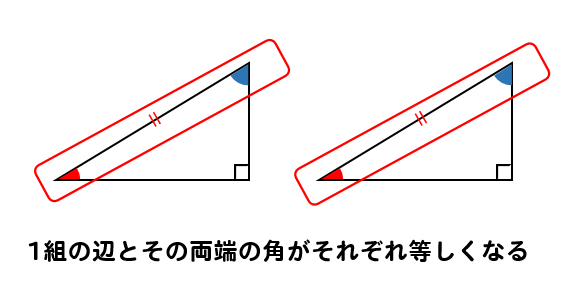
よって、斜辺と１つの鋭角が等しいことが分かった時点で

１組の辺とその両端の角がそれぞれ等しくなることが確定するということになります。

 

 

次は、『直角三角形の斜辺と他の１辺がそれぞれ等しい』場合を考えてみましょう。

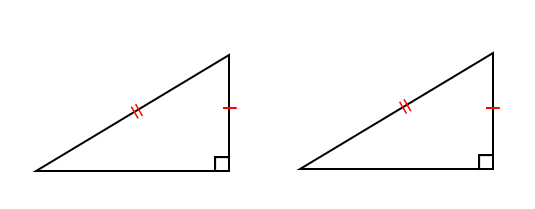
これに関しては、中３で学習する三平方の定理を知っておくと簡単に考えることができます。

直角三角形は２辺が等しい場合、残りの１辺も等しくなります。

詳しくは三平方の定理の記事をご参考ください(^^)

 

よって、３辺が等しくなりますね。

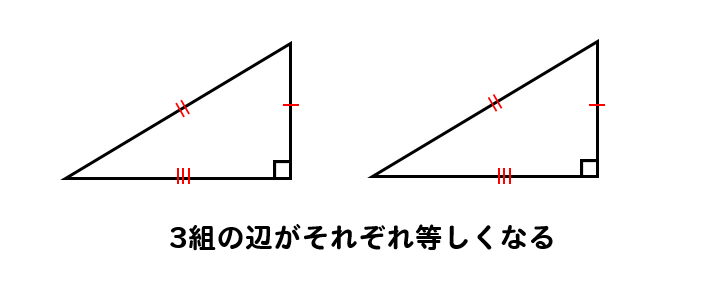
よって、斜辺と他の１辺が等しいことが分かった時点で

３組の辺がそれぞれ等しくなることが確定するということになります。

 

 

つまり、直角三角形の場合には

少しの情報だけで、通常の合同条件を導くことができるということになりますね。

そこから利用されるようになったのが『直角三角形の合同条件』です。

だから、考えていることは今まで通りなんだよ！ってことで理解しておきましょう。

 

合同な直角三角形を見つけてみよう！

それでは、いろんな直角三角形から合同な図形を見つける練習をしてみましょう。

 

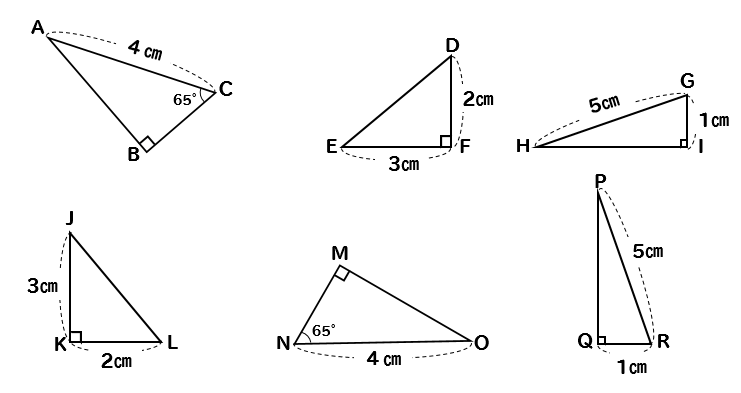
合同な直角三角形はコレだ！

 

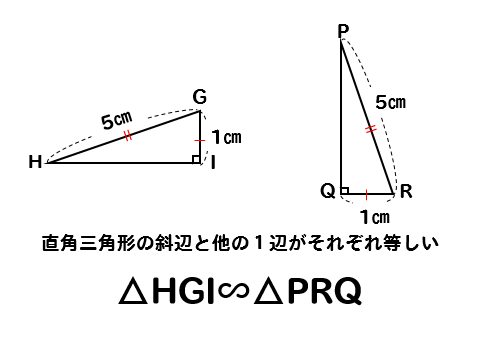
これらは斜辺が同じ長さになっている三角形に注目するとすぐに見つかりますね。

 

気をつけないといけないのがこちらです。

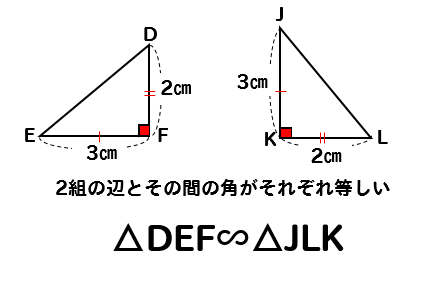
これらの直角三角形には、斜辺の長さが書いていないので

今まで通りの合同条件を使って考えるようになります。

 

 

直角三角形の合同条件が使えるのは

斜辺が等しいことが分かっているときだけなので注意しておきましょう！

 

直角三角形の合同証明の書き方とは

直角三角形の合同条件を利用した、合同証明の問題に挑戦してみましょう。

 

二等辺三角形の形

 

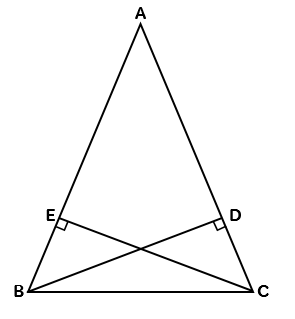
証明を書き始める前に、CD＝BEになる理由を考えていきましょう。

まず△BCEと△CBDに注目すると

仮定から

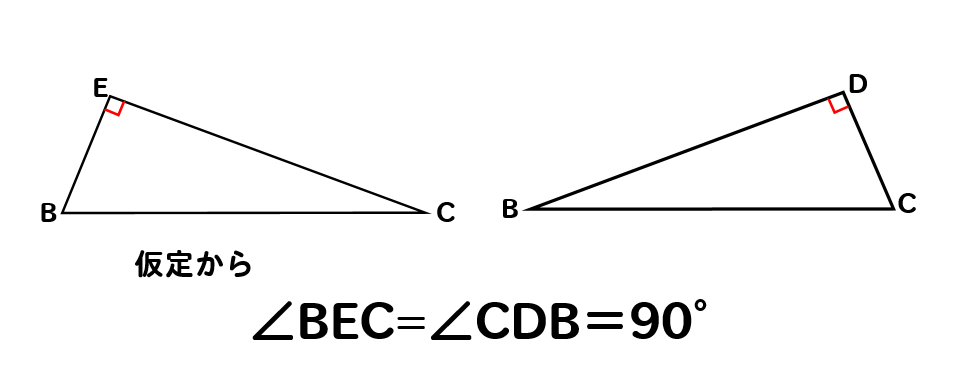
∠BEC=∠CDB＝90°だということがわかります。

あ、直角三角形だからちょっと楽な合同条件が使えるかな～って予想できますね。

 

次に、図を見ながら等しくなることろを自分で見つけていきます。

 

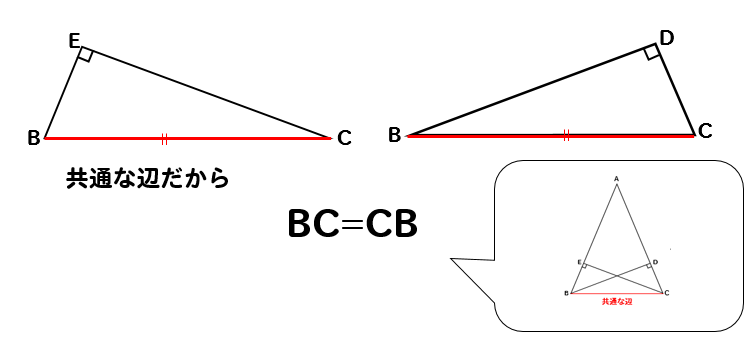
重なっている辺の長さは等しくなるんでしたね。

よって、BC=CBが見つかります。

 

次には△ABCが二等辺三角形であることから底角の大きさが等しくなります。

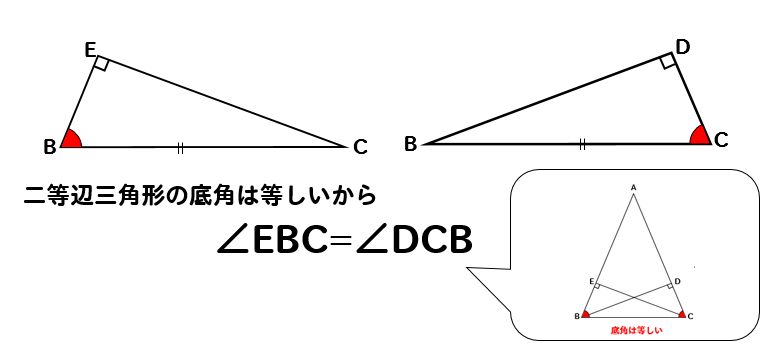
よって、∠EBC=∠DCBが見つかります。

 

 

以上のことをまとめると

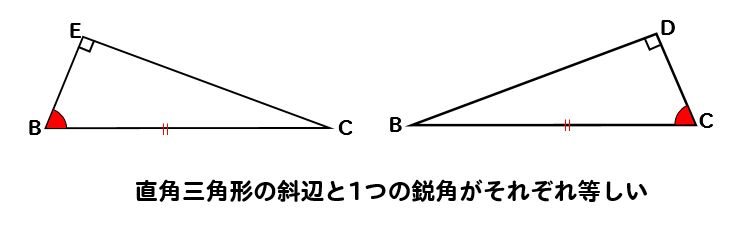
2つの直角三角形は、斜辺と1つの鋭角が等しくなるので

△BCE≡△CBDであることが分かりました。

 

よって、合同な図形は対応する辺の長さが等しくなるので

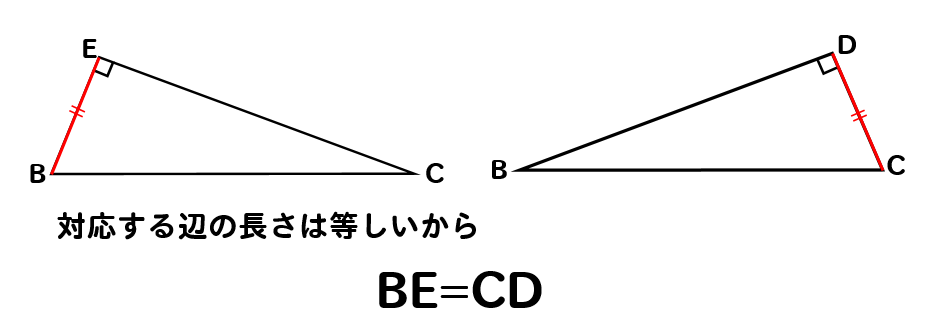
BE=CDであることが分かります。

 

さて、これでCD=BEとなる理由がわかったので

これらのことをまとめて証明問題を書いていきましょう。

 

証明問題の書き方の手順は

でしたね。

 

それでは、まとめていきます。

 

角の二等分の形

 

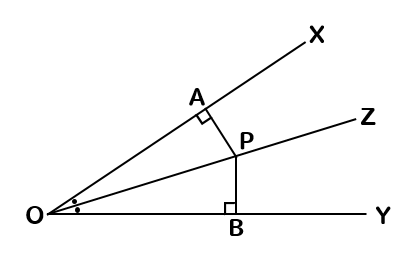
△OAPと△OBPに注目すると

仮定から分かることと、共通な辺を組み合わせると

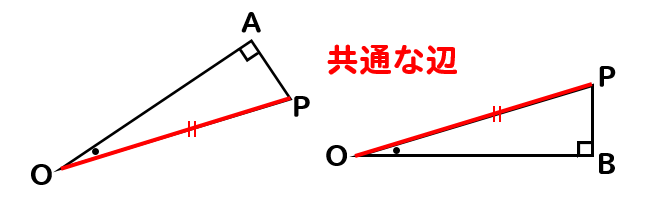
斜辺と1つの鋭角が等しくなるので

△OAP≡△OBPということが分かります。

よって、対応する辺の長さが等しくなるのでPA=PBとなります。

 

これをまとめて証明を書いていきましょう。

 

直角三角形を利用して二等辺三角形を証明する問題

次は、直角三角形の合同を利用して二等辺三角形になることを証明する問題を解説していきます。

まず、二等辺三角形になるための条件を復習しておきましょう。

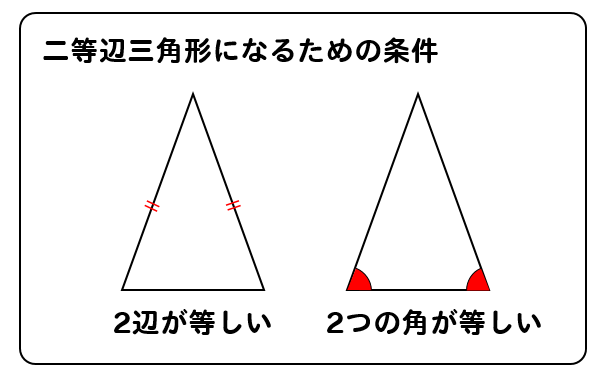
このどちらかの条件を満たせば、二等辺三角形であることを証明できます。

 

それでは、問題を見ていきましょう。

三角形ABCで、頂点B、Cからそれぞれ辺AC、ABに垂線BD、CEをひく。CE=BDならば△ABCは二等辺三角形であることを証明しなさい。

 

今回の証明の流れとしては

△BEC≡△CDBを示す。

対応する角の大きさは等しいから

∠EBC＝∠DCBとある。

 

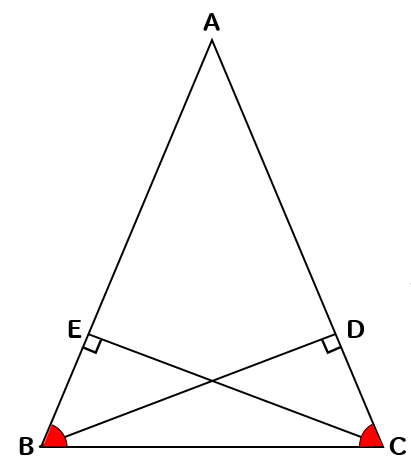
つまり、△ABCにおいて∠ABC＝∠ACBということになる。

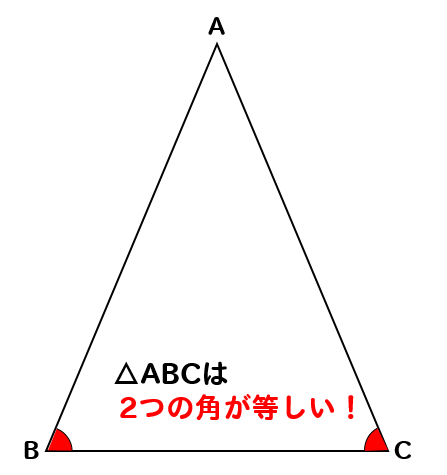
よって、2つの角が等しいから

△ABCは二等辺三角形だ！

 

 

それでは、このことをまとめて証明を書いていきます。

 

まとめ

お疲れ様でした！

直角三角形の合同条件を使いこなせるようになってきましたか？

最後にもう一度、合同条件を確認しておきましょう。

 

通常の合同条件に比べて、少しの情報で合同が言えるのでちょっと楽ができるというものでしたね。

ただし、斜辺が等しいことが分からないと使えない！

という制約もあるので気を付けてください。

斜辺が分からない場合には、直角三角形であっても通常の合同条件を利用するようにしましょう。

 

 

直角三角形をマスターしたら

二等辺三角形、正三角形、平行四辺形など

いろんな図形の特徴をマスターしていきましょう！