今回は中1で学習する『空間図形』の単元から
- 円錐の表面積を求める
- 展開したときのおうぎ形の中心角を求める
それぞれの問題を解説していきます。
問題
下の図の立体についてそれぞれ求めなさい。
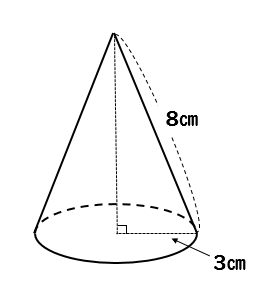
(1)この円錐を展開したときにできる側面のおうぎ形の中心角を求めなさい。
(2)この円錐の表面積を求めなさい。
体積や表面積を求める問題はよく目にすると思いますが
その中でも円錐を取り上げた問題が一番よく出題されます。
なぜなら、円錐の問題には
空間図形の知識だけでなく、おうぎ形の知識も一緒に問うことができるからです。
出題者としては、この1問で2つの問いかけができるので
とっても便利なんですね!
だけどね…
この円錐の問題
実はめっちゃくちゃ簡単に解くことができるんだよね!

ということで
今回は、教科書に載っている基本に忠実な解き方と
めっちゃ簡単に解くことができる裏ワザ公式のようなものを
それぞれ紹介していきます。
では、解説していくぞー!
側面の中心角を求める方法!
それでは、(1)の問題を使って
側面の中心角の求め方について解説していきます。
まず、円錐の展開図は
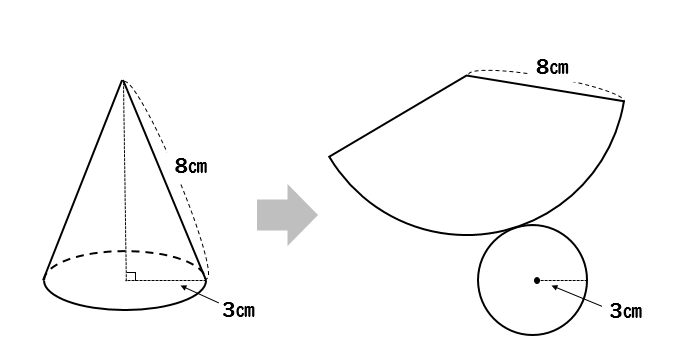
このように、おうぎ形と円が組み合わさった形になります。
そして、ポイントとなるのが
側面であるおうぎ形の弧の長さと
底面である円の円周の長さが等しくなります。
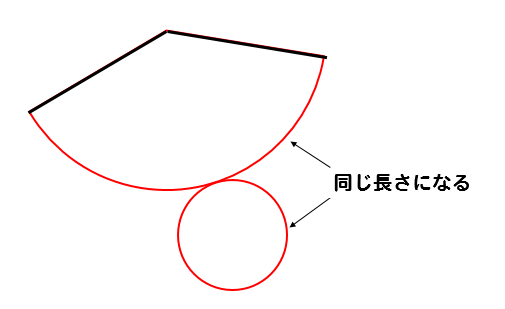
(側面の弧の長さ)=(底面の円周の長さ)
このことを利用して考えていきます。
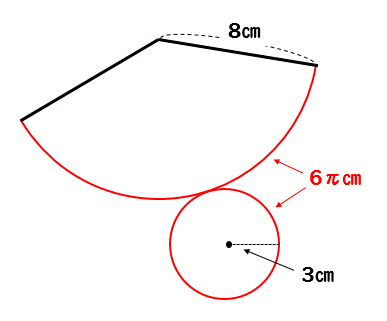
今回の問題では、底辺の半径が\(3\)㎝なので
円周の長さは\(6\pi\)㎝となります。
よって、おうぎ形の弧の長さも\(6\pi\)㎝となります。
ここまできたら
側面だけを取り上げて考えてみます。
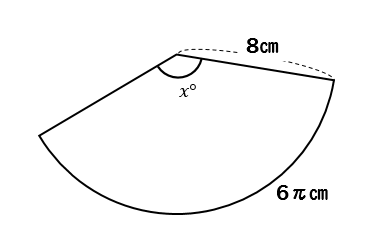
すると、側面であるおうぎ形は
半径\(8\)㎝、弧の長さが\(6\pi\)cmであるということがわかります。
ここからは、おうぎ形の中心角を求める問題ですね。
今回は方程式を使って求める方法で紹介します。
中心角を\(x\)として考えると
$$2\pi\times 8\times \frac{x}{360}=6\pi$$
8と360を約分してやります。
$$2\pi\times \frac{x}{45}=6\pi$$
両辺から\(\pi\)を消してやります。
$$\frac{2}{45}x=6$$
両辺に45をかけて分数を消します。
$$2x=270$$
$$x=135$$
よって、中心角は135°と求めることができました。
中心角の求め方をまとめておきましょう。
側面の中心角を求める手順
- 底面の円周の長さを求めて、側面の弧の長さを求める
- 弧の長さを利用して、おうぎ形の中心角を求める
以上!
これが基本に忠実な解き方です。
円錐の問題の中に、おうぎ形の問題が隠れているんですね。
非常にイイ問題、だけど厄介な問題です。

表面積を求める方法!
側面の中心角が求まったところで
次は円錐の表面積を求めていきます。
表面積というのは、展開図全体の面積のことですね。
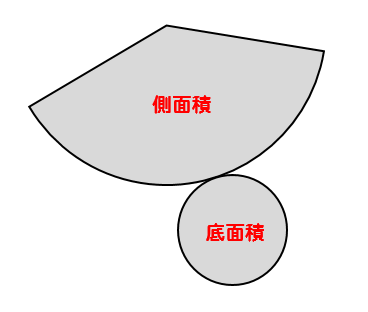
側面であるおうぎ形の面積と
底面である円の面積をそれぞれ求めて
合計してやれば、表面積の完成です!
それぞれ計算してやると
側面積は
$$\pi \times8^2\times \frac{135}{360}$$
$$=64\pi \times \frac{3}{8}$$
$$=24\pi$$
底面積は
$$\pi \times 3^2=9\pi$$
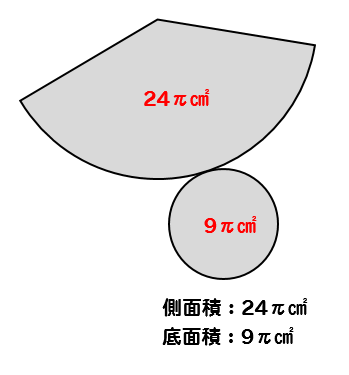
よって、表面積は
$$24\pi +9\pi=33\pi(cm^2)$$
となります。
(1)\(135°\)
(2)\(33\pi\)cm²

母線を使った裏ワザ公式とは!?
さて、円錐の表面積や中心角の求め方はご理解いただけましたか?
計算量が多いし、ちょっとややこしいですよね…

そんなあなたに活用してほしいのが
円錐の側面積と中心角を一瞬で求めてしまう裏ワザ公式です!
まぁ、受験ではほとんどの人がこの裏ワザ公式を利用することになると思います。
だって、めっちゃくちゃ簡単だから。
そんな裏ワザ公式とは
母線と半径の長さを利用して
$$(中心角)=\frac{(半径)}{(母線)}\times 360$$

このように求めてやることができます。
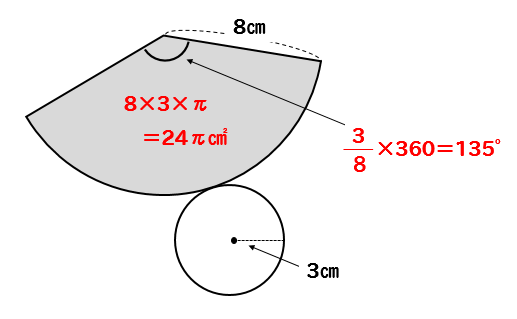
今回の問題であれば
側面積は
$$8\times 3\times \pi=24\pi$$
側面の中心角は
$$\frac{3}{8}\times 360=135$$
と求めることができます。
ホントに一瞬過ぎる…

ただし、注意してほしいのは
この裏ワザ公式で求めることができるのは
側面積だからね!!
表面積を求める問題であれば
裏ワザ公式で求めた側面積に底面積を足し合わせる必要があるから
そこのところを忘れないように!
円錐の裏ワザ公式
$$(中心角)=\frac{(半径)}{(母線)}\times 360$$
円錐の表面積、中心角 まとめ
お疲れ様でした!
裏ワザ公式が衝撃過ぎるよね…
基本に忠実なおうぎ形を利用した解き方も理解しておいて欲しいけど
テストのときには、この裏ワザ公式をぜひとも利用してほしい!
この公式を利用すれば
簡単に答えを出せるだけでなく
かなりの時間短縮にもなるから
他の問題に集中することができるよね
これで得点アップ間違いなしっ!
円錐の問題をたくさん解いて
裏ワザ公式を身につけちゃおう!
ファイトだー(/・ω・)/
















すっごいわっかりやすうううう!ほんとたすかるうううう!!!
円錐の公式は超大事だから
絶対に覚えておいてくださいね!!
わかりました
今回のやり方で表面積を求めるときは
24π+9πでいいんですか?
そうですね!
裏ワザ公式を使いこなせると
かなりラクになるのでお得ですね!
テストで側面積を5秒で出せましたっっっっ!ありがとうございます!!!!!
さすがです!!
それなジャパン
今までわかんなかったけどこれ見て理解できました!!とてもわかりやすかったです!
よかった^^
嬉しいコメントありがとうございます!
今年中学受験するので、円錐の表面積や中心角も覚えといたほうがいいかなと思ってこのサイトを拝見しました。メッチャわかりやすいです!ありがとうございます!
中学受験がんばってください!!