直方体、立方体の対角線の長さは公式でラクラク計算できるぞ！

今回の記事では、

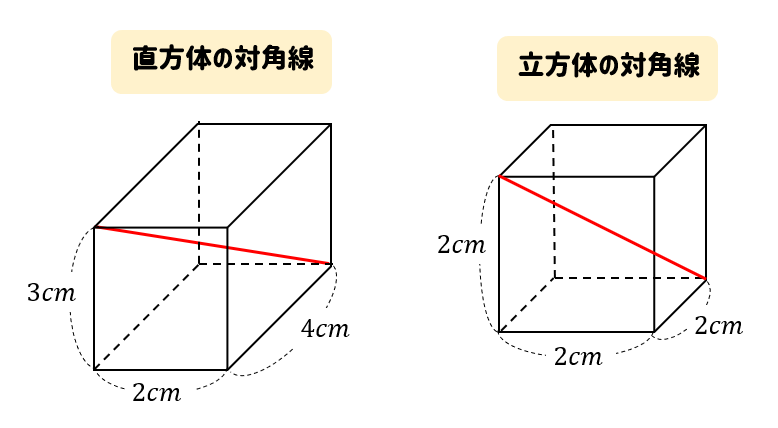
このように直方体や立方体の対角線を求める方法について解説します。

結論から言ってしまうと、

中学3年生で学習する三平方の定理を使って

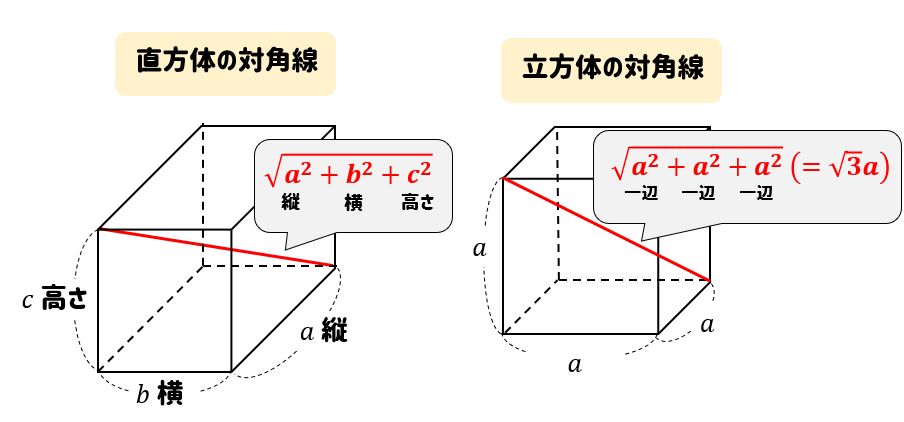
このように計算することができちゃいます。

こちらの問題であれば答えはこんな感じ！

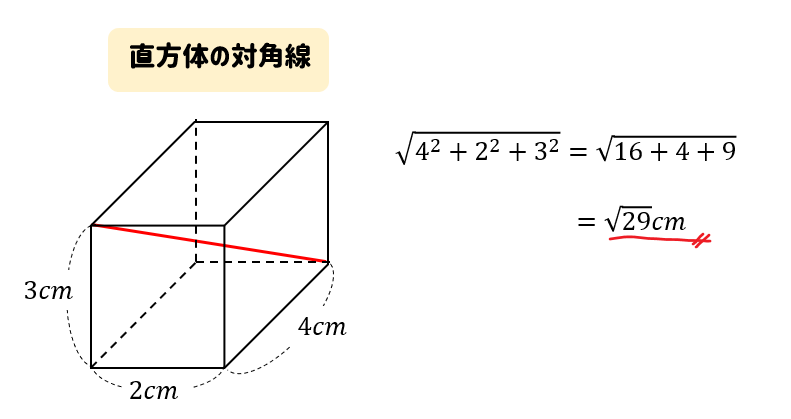
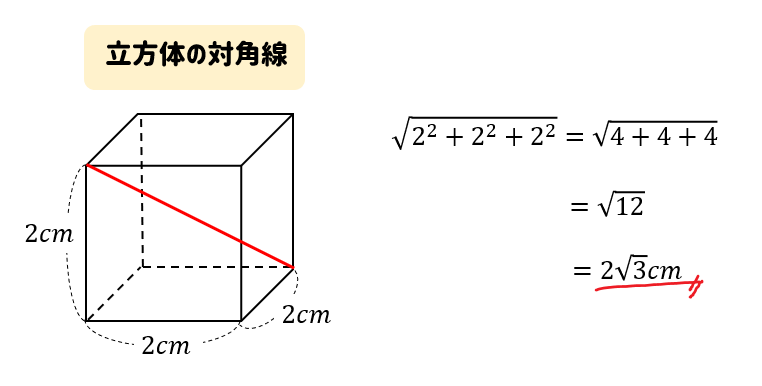
この公式を覚えてしまえば

楽勝で計算ができてしまうのですが、

なぜこのように計算することができるのか？

このことについて、イチから解説しておきますね！

直方体、立方体の対角線の長さを求める考え方

直方体、立方体の対角線を求めるには、

次のように2つの三角形に分けるて考えていきます。

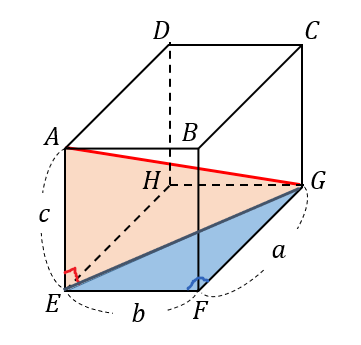
すると、赤い直角三角形に注目すると

求めたい対角線\(AG\)の長さは次のように表すことができます。

$$\begin{eqnarray} AG^2&=&AE^2+EG^2\\[5pt]AG&=&\sqrt{c^2+EG^2}\end{eqnarray}$$

でも、ここで\(EG\)の長さって何？？

となって困ってしまいます。

なので、次に底面を半分にした青い三角形に注目します。

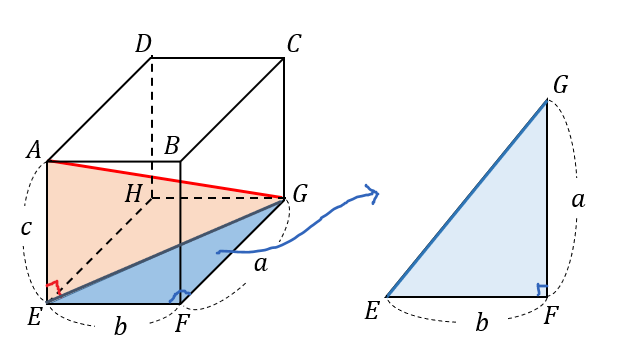
すると、\(EG\)の長さは次のように表すことができます。

$$\begin{eqnarray} EG^2&=&EF^2+GF^2\\[5pt]EG&=&\sqrt{a^2+b^2}\end{eqnarray}$$

よって、

$$\begin{eqnarray} AG&=&\sqrt{c^2+EG^2}\end{eqnarray}$$

$$\begin{eqnarray} EG&=&\sqrt{a^2+b^2}\end{eqnarray}$$

この2つの式を組み合わせることによって

$$\begin{eqnarray}AG(対角線)&=&\sqrt{c^2+EG^2}\\[5pt]&=&\sqrt{c^2+(a^2+b^2)}\\[5pt]&=&\sqrt{a^2+b^2+c^2} \end{eqnarray}$$

という公式を作ることができるわけですね(^^)

立方体の場合も同じように公式を作ることができます。

では、理解を深めるため

練習問題に挑戦してみましょう(/・ω・)/

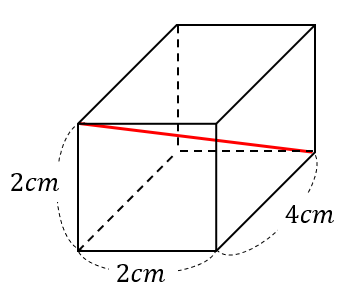
練習問題に挑戦！

次の対角線の長さを求めなさい。

まとめ！

お疲れ様でした！

直方体や立方体の対角線の長さは、

2つの直角三角形に注目することで求めることができます。

ですが、公式を覚えておけば

計算の手間をかなり省けるのでおススメです！

なので、公式をしっかりと使いこなせるようにしておきましょう(/・ω・)/