今回は中3で学習する
『相似の図形』の単元の中から
- どうやって相似な図形を見つけるの?
- 相似条件ってなに?
- どうやって問題を解くの?
という点について、基礎から解説をしていきます。
さぁ、いきましょー!
相似な図形の基本性質については、こちらの記事をご参考ください。
今回の内容はこちらの動画でも解説しています!
相似な図形を見つけるには?
相似な図形とは
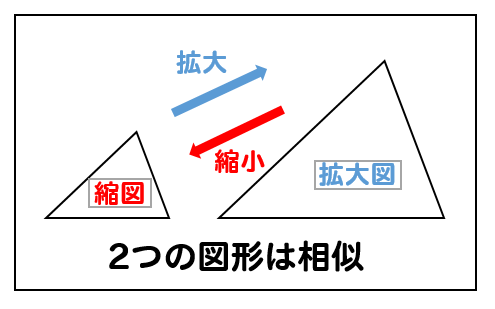

拡大、縮小されている図形のことでしたね。
ということは、2つの図形が相似であるかどうかを調べたいとき
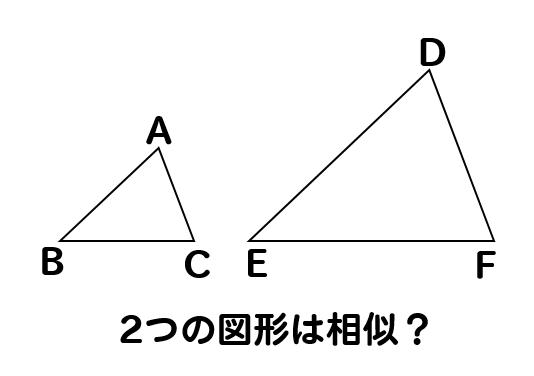

どちらか一方を、拡大または縮小して
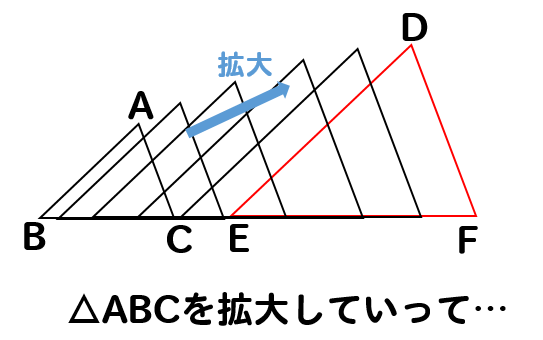

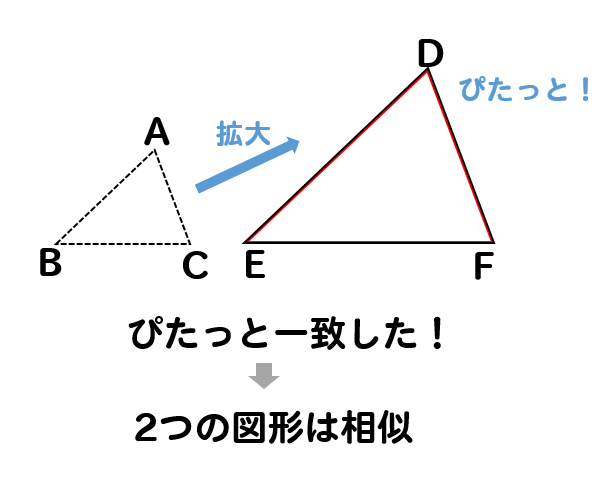

ぴったり一致させることができれば
相似である!と言えます。
一致しなければ、相似ではないということにもなります。
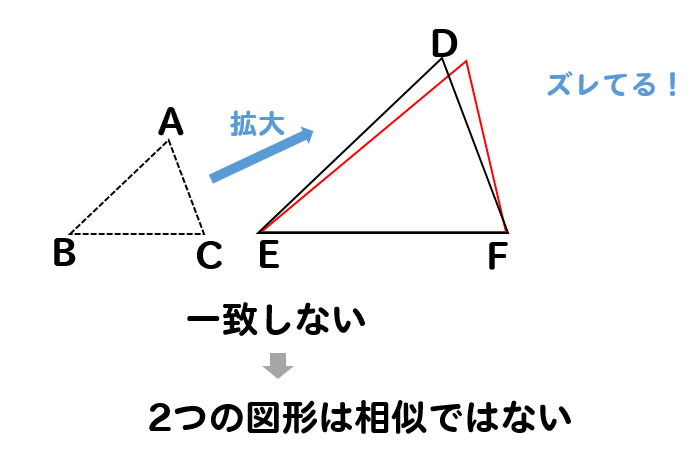

このように拡大、縮小してみれば
相似かどうかが分かるのですが
拡大、縮小って
そんなに簡単にできますか!?
今の時代


スマホやパソコンがあれば簡単にできちゃうのかもしれませんが
やっぱりめんどうですよね。
というわけで
わざわざ拡大、縮小をやらなくても
2つの図形が相似であるか
確かめる方法があれば便利だと思いますよね?
そして
その便利な確かめ方法というのが
『相似条件』と呼ばれるものです。
相似条件とは
実は、図形の辺の長さや角の大きさを比較するだけで
コレ相似!
コレ相似じゃない!
って瞬時に判断ができるんですね。
わざわざ拡大、縮小する必要なし!
辺の長さや角の大きさを比較したときの
判断基準となるものが『相似条件』です。
この条件を満たしていれば相似
満たさなければ相似ではない
と判断することができる条件です。
相似条件は以下の3つあります。
- 3組の辺の比がすべて等しい
- 2組の辺の比とその間の角がそれぞれ等しい
- 2組の角がそれぞれ等しい
いずれか1つでも満たしていれば
その瞬間に
ハイ、あなたたち相似でーす。


と判断することができるのです。
それでは、相似条件を1つずつ確認していきましょう。
3組の辺の比がすべて等しい
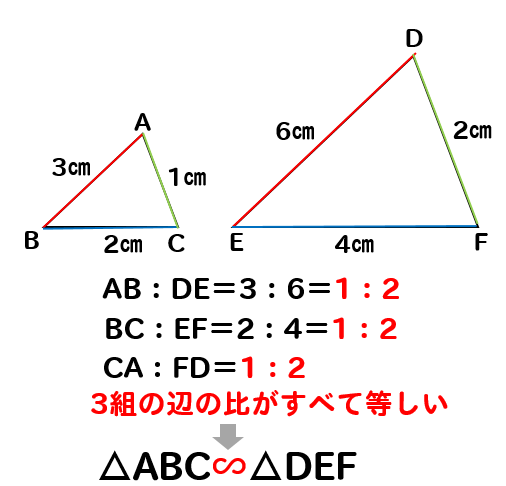

対応しそうな3組の辺をそれぞれ比較してみて
辺の長さの比がすべて等しくなれば相似だということが分かります。
2組の辺の比とその間の角がそれぞれ等しい
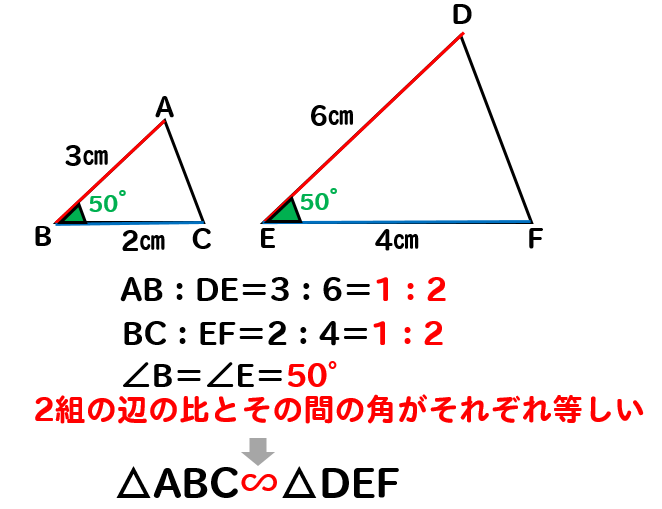

2組の辺の比と
それに挟まれている角の大きさがそれぞれ等しいとき
2つの図形は相似だということが分かります。
2組の角がそれぞれ等しい
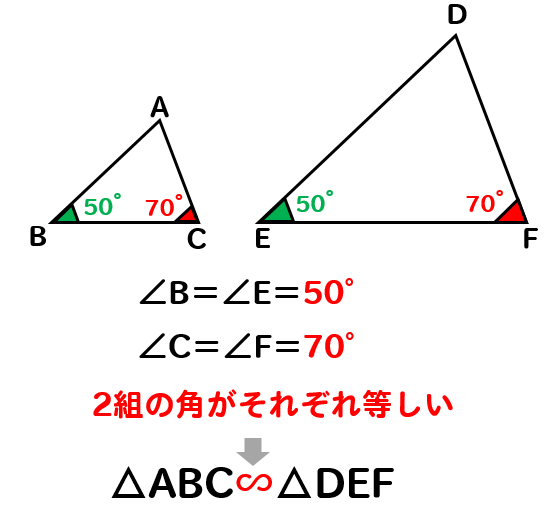

これが一番単純でわかりやすいです。
2つ角の大きさが等しいと確認できれば
それで相似であることが分かります。
このように
図形の長さや角の大きさを比較するだけで
2つの図形が相似になるかどうかを調べることができます。
ただし、この3つの条件をちゃんと覚えておかないと
相似かどうかの判断が下せないので
相似条件はしっかりと覚えておきましょう。
それでは
これからの相似条件を使って
相似な図形を見つける練習をしましょう。
相似な図形を見つける問題
それでは、良く出てくる問題に挑戦してみましょう。
次の図で、相似な三角形を見つけ、記号で表しなさい。
(1)
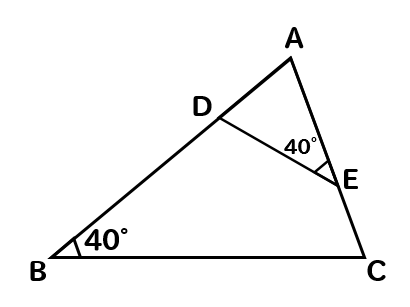

(2)
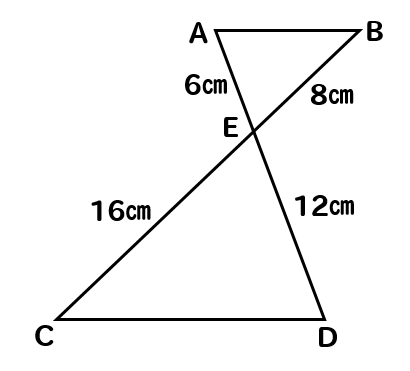

(3)
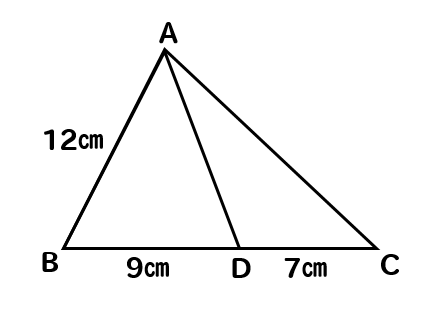

(1)の解説!
(1)


この図形の中には、三角形が2つ隠れています。
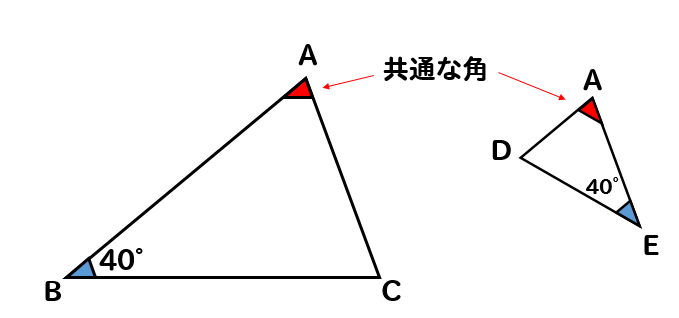

それぞれの三角形を見比べると
∠B=∠E=40°
共通な角だから
∠A=∠A
ということがわかります。
よって
2組の角がそれぞれ等しいので
△ABC∽△AED
(2)の解説!
(2)


この図形の中に隠れている2つの三角形を見比べると
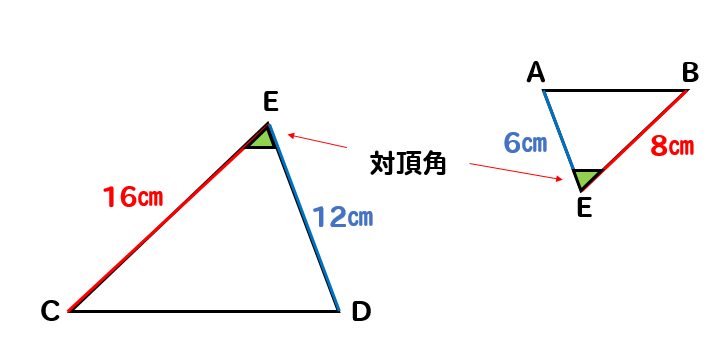

EC:EB=16:8=2:1
ED:EA=12:6=2:1
2組の辺の比がそれぞれ等しいです。
そして
対頂角は、角の大きさが等しくなるので
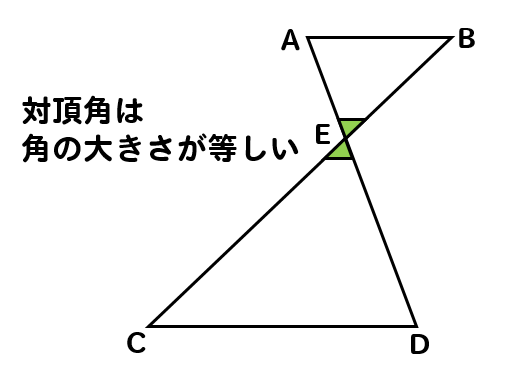

2組の辺の間にある∠Eが等しくなります。
∠E=∠E
以上のわかったことをまとめると
2組の辺の比とその間にある角がそれぞれ等しいので
△AEB∽△DEC


(3)の解説!
(3)


この図形の中には3つの三角形が隠れています。
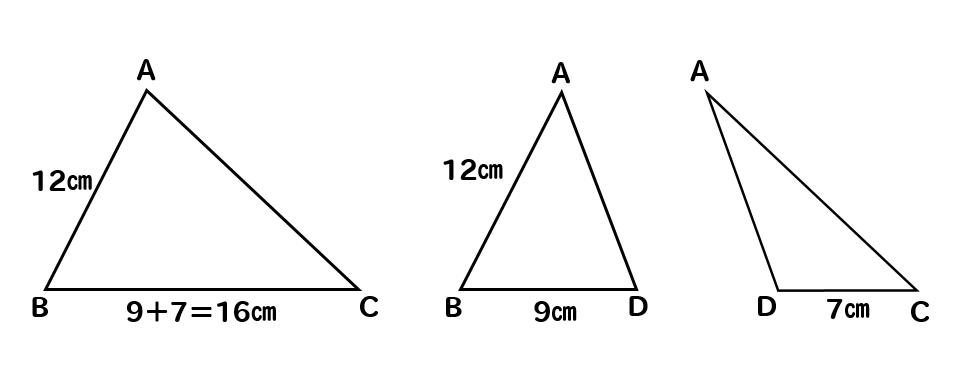

この中から、どれが相似になるのかを見極めていかないといけません。
パッと見だと、どれが同じ形になるのか分かりにくいですね。


これだけだとわかりにくいので
共通の角を見つけて、等しくなる角に印をつけてみましょう。
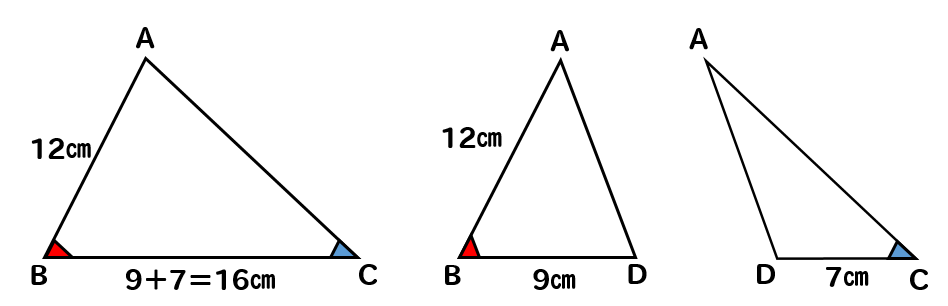

それぞれの三角形を見てみると
△ABCは2辺、2角
△ABDは2辺、1角
△ADCは1辺、1角の情報がわかりました。
この3つの中から相似な図形を見つけるときに
情報が少ない図形は、相似条件に当てはめることができません。
なので、情報が多く揃っている
△ABCと△ABDが相似になるだろうな、と予想して
この2つの三角形が、相似条件に当てはまるかを確かめていきます。
どれが相似な図形なのか判断がつきにくいときは
辺の長さや角の大きさが、たくさんわかっている図形に注目しましょう!
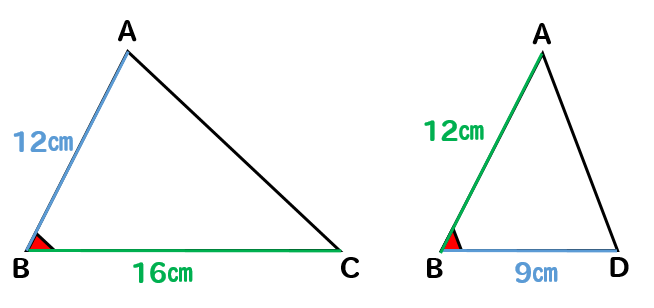

AB:BD=12:9=4:3
BC:BA=16:12=4:3
共通な角だから
∠B=∠B
よって、2組の辺の比とその間の角がそれぞれ等しいので
△ABC∽△DBA
相似条件 まとめ
相似な図形を見つけるためには
辺の長さや角の大きさを比較して
- 3組の辺の比がすべて等しい
- 2組の辺の比とその間の角がそれぞれ等しい
- 2組の角がそれぞれ等しい
のいずれかの条件を満たせば
相似であると判断することができます。
どの条件に当てはめればよいのか困ったときには
図形の分かっている辺の数に注目して
3本わかっている
⇒3組の辺の比がすべて等しい
2本わかっている
⇒2組の辺の比とその間の角がそれぞれ等しい
1本わかっている
⇒1組の辺の比とその間の角がそれぞれ等しい
このように判断して調べてみると
問題が解きやすくなるはずです(^^)
相似条件は分かってもらえたと思うので
たくさん問題を解いて理解を深めていってくださいね。
相似条件が理解できたら次はちょっと応用ですね。
ファイトだー!!
相似な図形の見つけ方、相似条件とは?←今回の記事



















めちゃくちゃ分かりやすかったです。ありがとうございます!
ありがとうございます(^^)
ステキなコメント
記事更新の原動力になります!
私は相似は苦手だったのでこのサイトを見てわかりやすくて理解できました。