【高校入試 数学】小問集合を問題演習！～第５回～

高校入試対策演習

小問集合の第５回目です！

目安時間は5分です。

挑戦してみましょう(^^)

第5回　小問集合

 

（1） \(10x-x\) を計算しなさい。

 

（2）二次方程式\(3x^2+7x+1=0\)を解きなさい。

 

（3）\(\sqrt{10}\)より小さい自然数をすべて書きなさい。

 

（4）変数\(x,y\)について、\(x\)と\(y\)の関係を表した次の式のうち、\(y\)が\(x\)に比例する関係を表した式はどれか。次のア～エからすべて選び、その記号を書きなさい。

ア　\(y=3x\)

イ　\(\displaystyle y=\frac{x}{3}\)

ウ　\(y=x+3\)

エ　\(y=3x^2\)

 

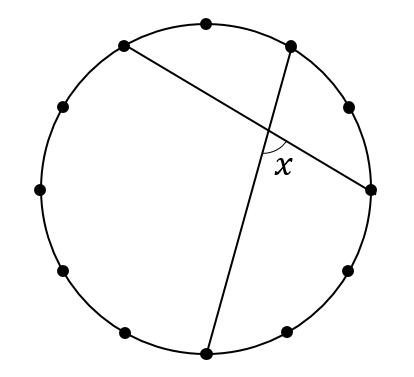
（5）下の図で、円周上の12点は円周を12等分している。\(∠x\)の大きさを求めなさい。

問題が解けた人は↓で答え合わせをしていきましょう！

問題の解答

解答はこちらです。

答え合わせしてみましょう(^^)

間違っていた部分は解説を見て

理解を深めておこう！

問題の解説

それでは各問題の解説をしていきます。

間違っていたところは念入りに確認しておきましょう！

（1）の解説！

これは普通に文字式の引き算なのですが

非常に間違いの多い問題です。

それは…

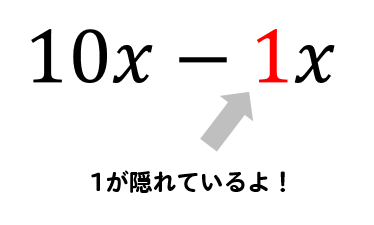
\(x\)の係数である1の存在を忘れてしまう人が多いからですね。

ちゃんと1があることを意識して計算できれば大丈夫！

$$10x-x=(10-1)x=9x$$

（2）の解説！

二次方程式はいくつか解き方のパターンがありましたが

今回の方程式は、解の公式を使って解くパターンになります。

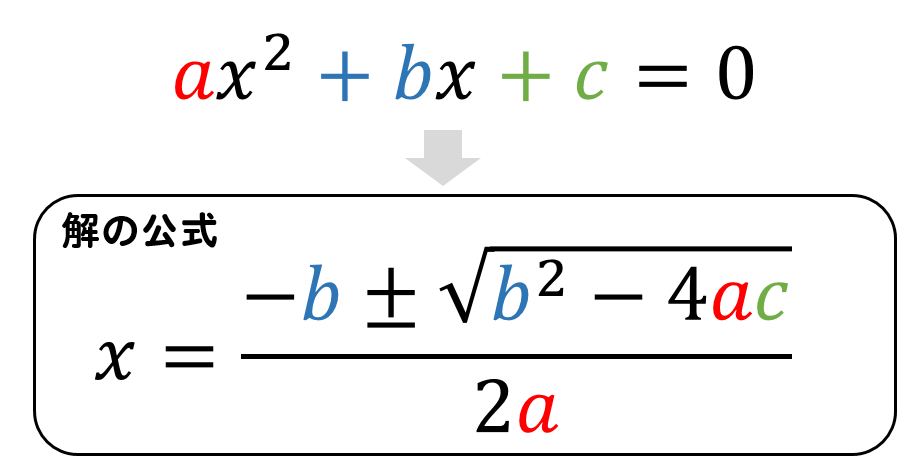
$$x=\frac{-7\pm \sqrt{7^2-4\times 3\times 1}}{2\times 3}$$

$$x=\frac{-7\pm \sqrt{49-12}}{6}$$

$$x=\frac{-7\pm \sqrt{37}}{6}$$

（3）の解説！

まず、自然数って何だっけ？

意外と忘れている人が多いので確認しておきましょう。

自然数とは、正の整数のことでしたね。

正の整数と言われてもピンときにくいですが

要は

１、２、３、４、５、６・・・

というような数のことです。

気をつけたいのは０はダメってこと！

ココを勘違いしている人が多いので気を付けてください。

それでは、問題に戻って

$$\sqrt{9}<\sqrt{10}<\sqrt{16}$$

$$3<\sqrt{10}<4$$

よって\(\sqrt{10}\)は、３と4の間の数だということが分かるね。

だから、それよりも小さい自然数となると

１、２、３となります。

（4）の解説！

式の形を見て、どの関数になるのかを判断する問題です。

それぞれの式の特徴を覚えておかないといけませんね。

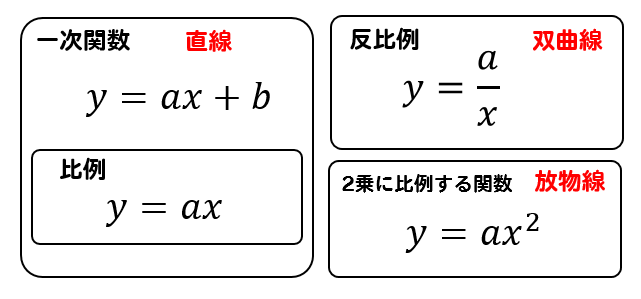
今回は比例になる式を選べということなので

式を見て、\(y=ax\)の形になっているものを見つけます。

すると

ア　\(y=3x\)　イ　\(\displaystyle y=\frac{x}{3}\)

が答えとなります。

ちなみに

ウ　\(y=x+3\)は一次関数

エ　\(y=3x^2\)は二乗に比例する関数ですね。

（5）の解説！

（5）下の図で、円周上の12点は円周を12等分している。\(∠x\)の大きさを求めなさい。

『何等分する』というような問題は

円周角の定理を使った問題の解き方をパターン別に解説！

こちらでも解説しておりますが

１区画分の中心角、円周角を求めることからスタートしましょう。

12等分の場合

1区画分の中心角は\(360\div 12=30°\)

円周角は中心角の半分だから\(30\div 2=15°\)となります。

それでは

この角度を利用して考えていきます。

図の中に補助線をひいて

赤い部分の弧に対する円周角を考えると

2区画分の場所だから

円周角は\(15\times 2=30°\)となります。

同様に、今度は緑部分の円周角を考えると

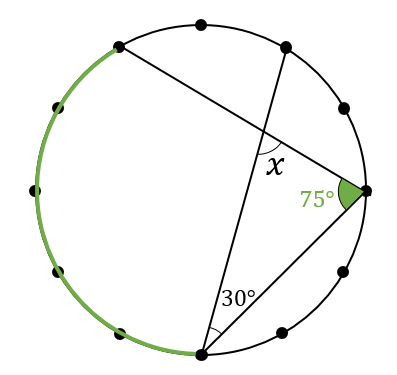
円周角は\(15\times 5=75°\)となります。

ここから\(x\)を含む三角形に注目すると

\(x=180-75-30=75°\)となります。

以上

小問演習の第5回でした。

全部解けた人は素晴らしい！

解けなかった人も必ず見直しをして

入試本番では解けるようにがんばっていこう！

ファイトだー(/・ω・)/