高校入試対策演習
小問集合の第3回目です!
目安時間は5分です。
挑戦してみましょう(^^)
第3回 小問集合
(1) \(\displaystyle 12\times \left(\frac{1}{3}-\frac{3}{4}\right )\) を計算しなさい。
(2)\(\displaystyle 1+\frac{a}{3}=2b\)を\(a\)について解きなさい。
(3)関数\(\displaystyle y=\frac{1}{4}x^2\)で、\(x\)の変域が\(-2≦x≦4\)のとき、\(y\)の変域を求めなさい。
(4)2つのさいころを同時に投げるとき、出る目の数の和が素数である確率を求めなさい。
(5)下の図は三角柱である。辺ACとねじれの位置にある辺をすべて答えなさい。

問題が解けた人は↓で答え合わせをしていきましょう!
ひこ数スタの無料メルマガ講座では、
毎週金曜に、小問演習のプリント&解説動画をお届けしています。
数学の力を伸ばすためには問題演習が欠かせません。
登録は無料ですので、ぜひご活用ください^^
登録直後にこれまでに配信してきた小問課題をまとめてプレゼント。
今すぐ演習にとりかかれますよ!
問題の解答
解答はこちらです。
答え合わせしてみましょう(^^)
答え
(1)\(-5\)
(2)\(a=6b-3\)
(3)\(0≦y≦4\)
(4)\(\displaystyle \frac{5}{12}\)
(5)\({辺}BE,{辺}DE,{辺}EF\)
間違っていた部分は解説を見て
理解を深めておこう!
問題の解説
それでは各問題の解説をしていきます。
間違っていたところは念入りに確認しておきましょう!
(1)の解説!
この問題で気をつけないといけないのは
この問題では、分配法則を使って計算していきましょう。
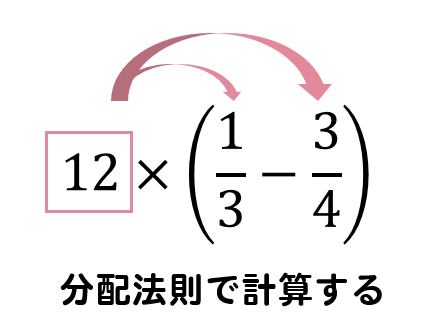
かっこの中の分数を通分して計算しても良いのですが
分配法則を利用した方が圧倒的に楽に計算できます。
$$\LARGE{12 \times \frac{1}{3}+12\times \left ( -\frac{3}{4}\right )}$$
$$\LARGE{=4-9}$$
$$\LARGE{=-5}$$
(2)の解説!
\(a\)について解きなさいということで
等式を変形しながら\(a=…\)の形を作っていきましょう。
まずは、分数の形がちょっとイヤなので
分数を消すために分母にある3を両辺に掛けます。
$$\LARGE{\left ( 1+\frac{a}{3} \right ) \times 3=2b \times 3}$$
$$\LARGE{ 3+a =6b}$$
分数の形が消えたら、3を右辺に移項します。
$$\LARGE{ a =6b-3}$$
完成!!
等式変形が苦手な人は
こちらで練習をしておきましょう!
(3)の解説!
変域は表を使って求めると楽ですね!
\(-2≦x≦4\)は0を含んでいるので、-2、0、4の値を求めます。
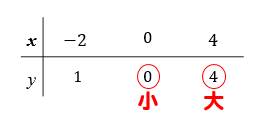

すると、\(y\)の値は一番大きいのが4、一番小さいのが0となるので


変域はこのように表すことができます。
変域問題は、答えを求めることがとっても簡単なのですが
その仕組みを理解しておくことが大切です。
なぜこのように求めるのか分からない方はこちらの記事もご参考くださいね!
(4)の解説!
2つのさいころの確率を考える場合には
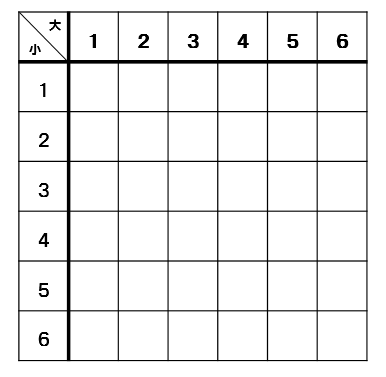

このような表を埋めることで求めていきましょう。
表を見ながら、2つの目の和が素数になるところに印をつけていきましょう。
ちなみに素数というのは
2、3,5、7、11・・・というような
1と自身の数でしか割り切ることができない数のことでしたね。
表に印をつけると
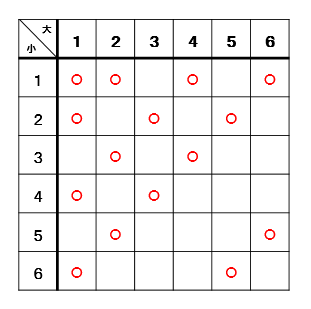

15個印がついたので
確率は\(\displaystyle \frac{15}{36}=\frac{5}{12}\)となります。
(5)の解説!
(5)下の図は三角柱である。辺ACとねじれの位置にある辺をすべて答えなさい。


ねじれの位置とは
平行ではなく、交わることもない位置関係のことでしたね。
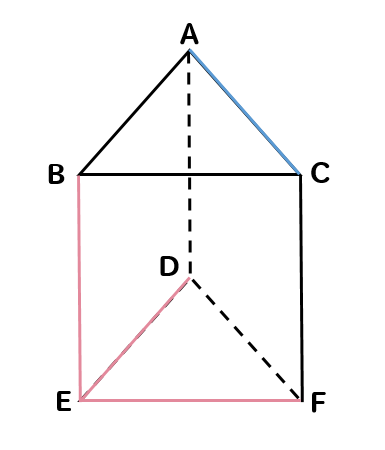

すると、このように
\({辺}BE,{辺}DE,{辺}EF\)がねじれの位置になることがわかります。
以上
小問演習の第3回でした。
全部解けた人は素晴らしい!
解けなかった人も必ず見直しをして
入試本番では解けるようにがんばっていこう!
ファイトだー(/・ω・)/
小問演習~第4回~はこちら!




















コメントを残す