今回は中3で学習する
『相似な図形』の単元から
中点連結定理を利用した問題について解説していきます。
特に、三角形を三等分するような問題がよく出題されているので
それを取り上げて、基礎から解説していきます。
ちなみに
相似な図形の他記事についてはこちら
基礎が不安な方は参考にしてみてくださいね。
それでは、中点連結定理いってみましょー!
今回の内容はこちらの動画でも解説しています(‘◇’)ゞ
中点連結定理とは
中点連結定理とは?
難しそうな名前ですが、実は単純な話です。
中点(真ん中の点)を
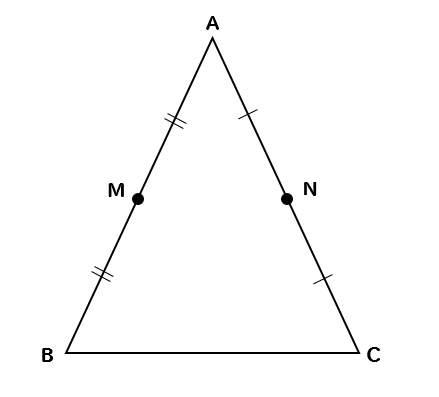

連結(つなげる)すると
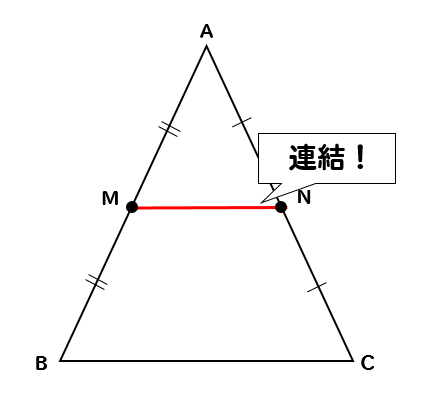

どんな特徴がある?
これが中点連結定理の意味です。
そして、中点を連結するとこのような特徴があります。
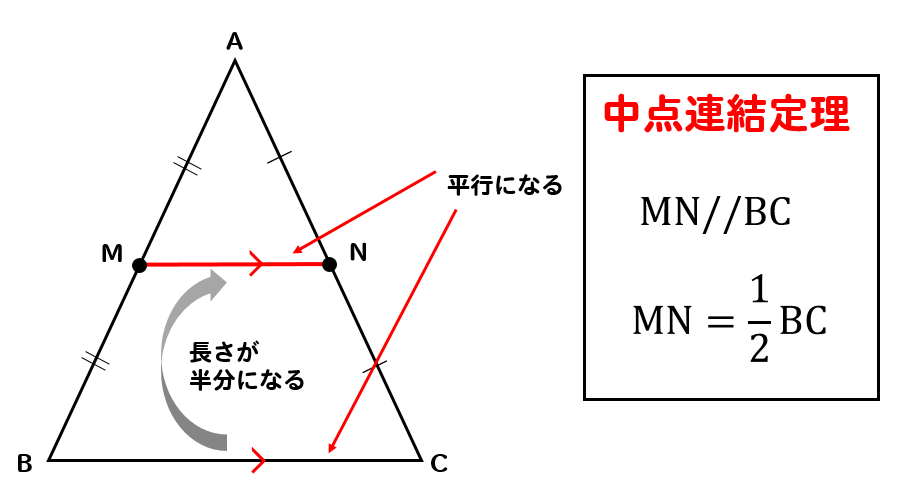

連結してできたMNの辺は
BCと平行になり、長さはBCの半分になるという特徴があります。
これを中点連結定理といいます。
中点を連結したら
『平行になって、長さが半分になる』
コレだけです。
ちょっと具体的に見てみるとこんな感じです。
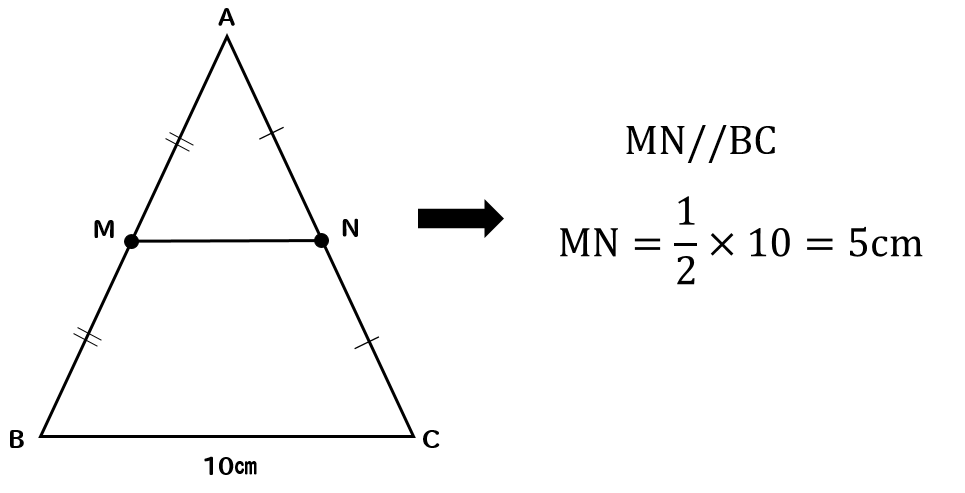

MNの長さはBCの半分になるので
$$\frac{1}{2}\times10=5cm$$
長さを半分にするだけです。
そんなに難しい話ではないですよね。
それでは、よく出題される三等分の問題について解説していきます。
三角形を三等分した問題の解説!
ADを三等分した点をF、Eとする。BC=CD、GF=5㎝のとき、BGの長さを求めなさい。
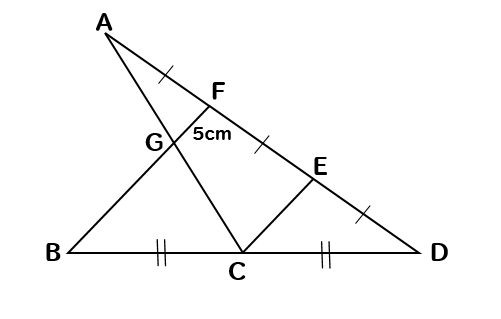

いろんな三角形が重なっていて複雑そうに見えますね。
まずは、△ACEに着目します。
するとGとFはそれぞれの辺の中点なので
中点連結定理が使えます。
(GがACの中点になる理由は後ほど説明します)
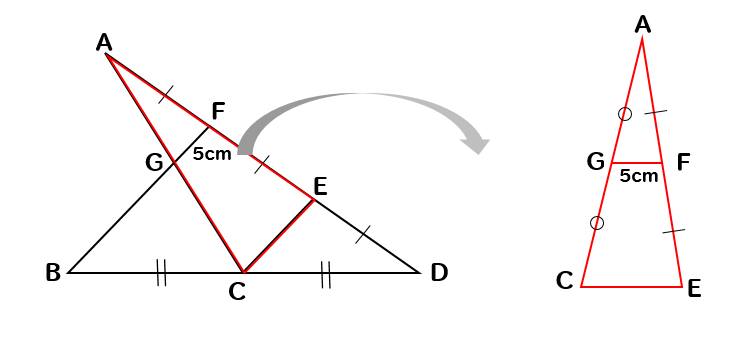

すると
$$CE=GF\times2=5\times2=10cm$$
と求めることができます。
次に△FBDに着目すると
こちらもCとEはそれぞれの中点になっているので
中点連結定理より
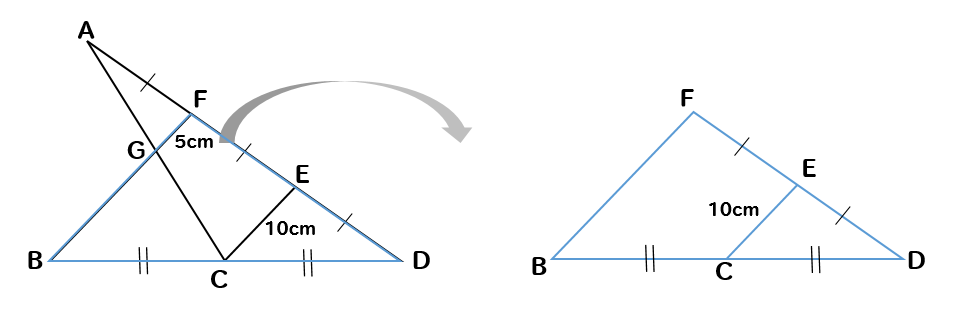

$$BF=CE\times2=10\times2=20cm$$
これでBFの長さが求まりました。
求めたいBGの長さは
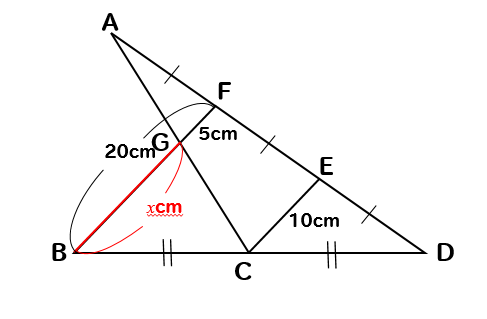

$$BG=BF-GF=20-5=15cm$$
このように求めることができます。
三角形を三等分するような問題では
2つの三角形に着目して
中点連結定理を使ってやると求めることができます。
長さを求める順番はこんなイメージです。
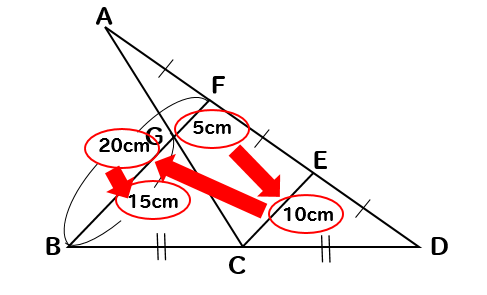

中点連結定理を使って
GF⇒CE⇒BF⇒BG
このように辿って求めていきます。
計算は辺の長さを2倍していくだけなんで
考え方がわかれば、すっごく簡単ですね!
最後に、なぜGがACの中点になるのか説明しておきます。
問題が解ければ、それでいいやっ!
っていう人は読み飛ばしてもらっても良いです。
…ほんとはちゃんと理解してほしいけど(-“-)笑


練習問題で理解を深める!
それでは、三等分問題を練習して理解を深めていきましょう。
問題
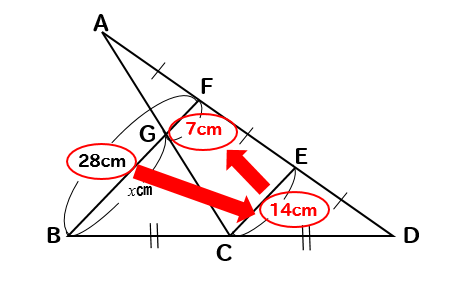
下の図で、xの値を求めなさい。
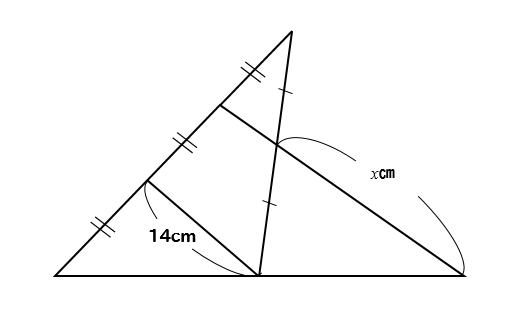

問題
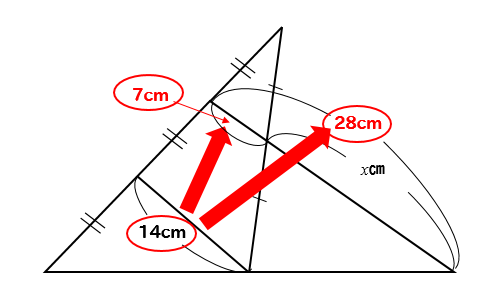
下の図で、xの値を求めなさい。
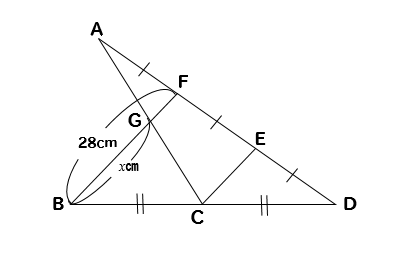

中点連結定理 まとめ
中点を連結させると


平行で、長さが半分になる!
コレだけしっかりと覚えておきましょう。
問題文の中に、○等分やAB=BCのように
中点をイメージする言葉が入っているときには
中点連結定理の使いどころです。
あ!中点連結定理だ!


って気づくことができれば楽勝な問題です。
入試にもよく出される定理なので
練習を重ねて必ず解けるようにしておきましょう!
ファイトだー!
中点連結定理を使った問題を解説!←今回の記事




















2問目の問いの答えが違うと思います。
ご丁寧にご指摘ありがとうございました!
問題文の長さを変更させてもらいました。
深く考えると
難しいですね
ほんとにね!
シンプルに考えていきましょ!