【中3数学】展開の公式のやり方は？問題を使って徹底解説！

今回は中３で学習する展開の計算について解説していきます！

 

この展開の計算とは、今後学習していく単元で必須となってくる計算方法の１つです。

しっかりとマスターしておきたいですね(^^)

スポンサーリンク

式を展開するとは？分配法則を使って計算

このような式の計算方法を覚えていますか？

$$\LARGE{3x(2x+y)}$$

かっこにかけ算や割り算がくっついているときには

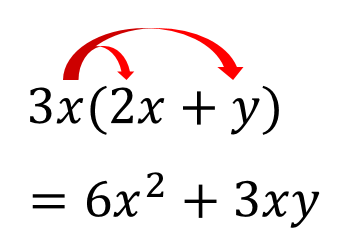
このように分配法則を使って計算していくのでしたね！

 

では、このような式の場合はどうでしょうか？

$$\LARGE{(a+2)(b-1)}$$

かっことかっこをかけ算をする場合

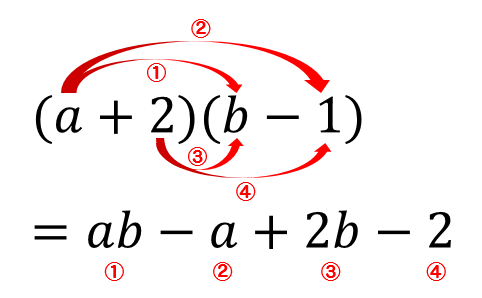
このように分配法則を使って計算していきます。

 

計算が多くて面倒ですけど、複雑な計算ではありませんね^^

このようにかっこの掛け算を分配法則を利用して、バラバラの状態にしていく計算のことを式を展開するといいます。

 

 

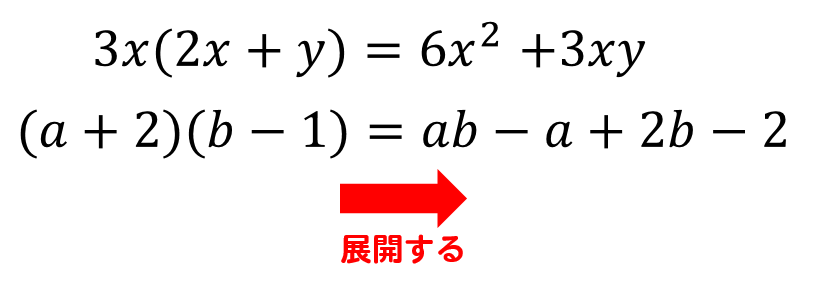
もっと正確にいうと

単項式や多項式に積の形をした式を、かっこをはずして単項式の和の形にすることを展開といいます。

 

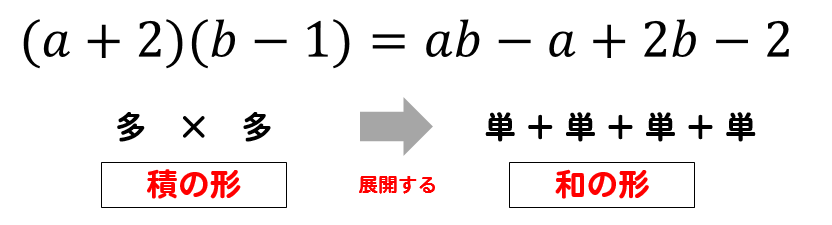
それでは、式の展開を練習してみましょう！

展開をラクにする乗法公式

展開の計算方法は理解してもらえましたか？

でも、ぶっちゃけ…

めんどいよねｗ

計算が多い！

 

少しラクして計算できないかな…

ということで登場するのが乗法公式！というものです。

乗法公式①

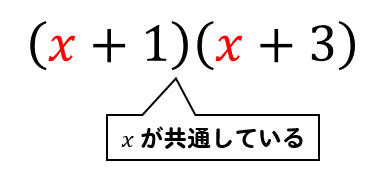
このように展開したい式のかっこの中に、共通しているパーツが含まれているときには、ちょっとラクをして計算することができます。

 

 

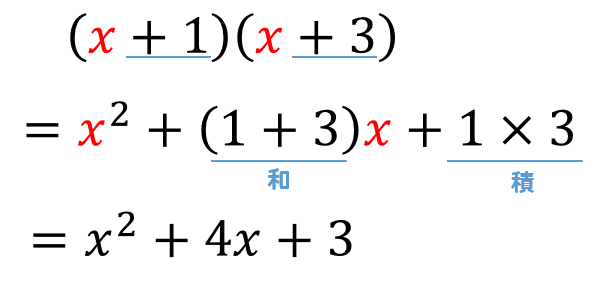
これが慣れてくると暗算で計算ができるようになってきます。

というわけで、練習問題を通して公式をマスターしていきましょう。

 

バッチリでしたか？^^

次はちょっとした応用も見ておきましょう。

かっこの中の共通しているパーツが次の式のように係数付きの場合

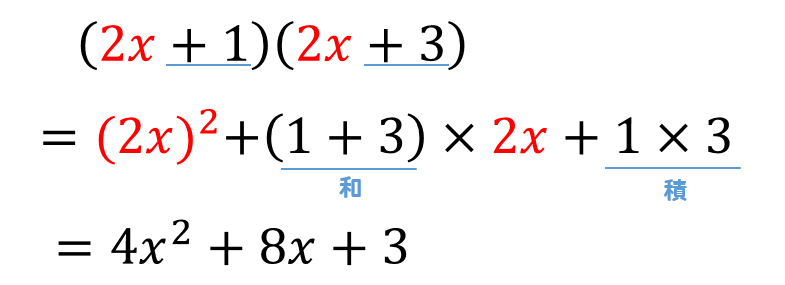
ちゃんと係数も忘れずに計算していきましょうね！

それでは、こちらも練習しておきましょう。

乗法公式②

次は展開したい式のかっこの中身が

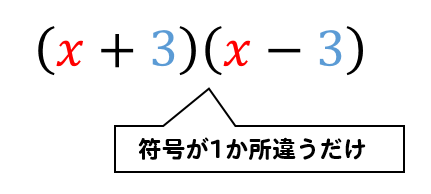
このように、1か所符号が違うだけで他が全く同じになっている場合

 

展開をすると

必ず真ん中部分が消えてしまいますよね。

それなら初めから、真ん中部分の計算は無視してやればOKです。

 

ということで、このように展開してやればラクに計算することができますね。

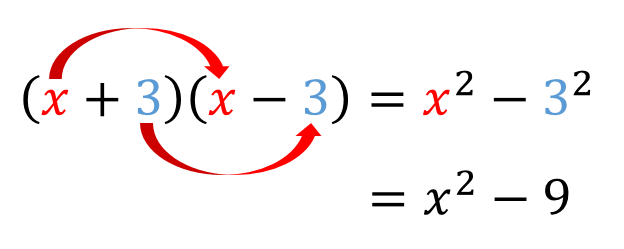
それでは、練習問題を通して公式をマスターしていきましょう。

乗法公式③

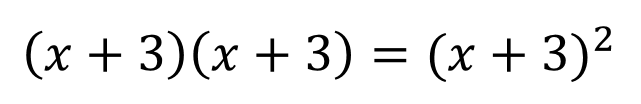
このように同じかっこどうしを計算するときには2乗の形を使って表します。

 

そして、同じかっこどうしを展開すると

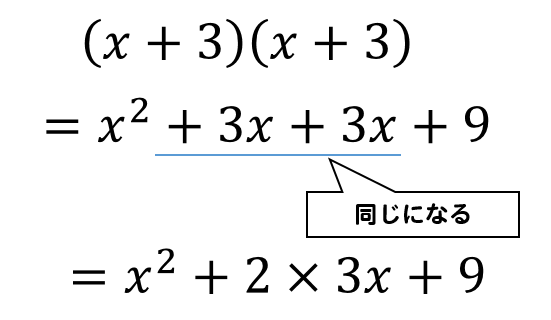
必ず真ん中部分で同じパーツが出てくることが分かりますよね。

それなら初めから真ん中部分は2倍してやればいいじゃん！

ということで、2乗の展開が出てきたら次のように計算していきましょう。

 

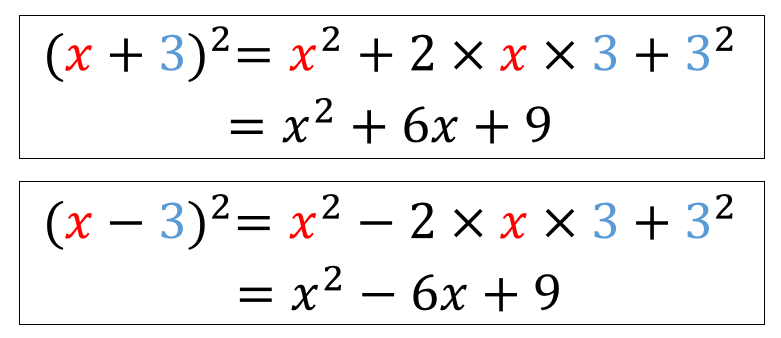
それでは、練習問題を通して2乗の展開公式をマスターしていきましょう。

 

以上で、中学で学習する展開公式は完了になります＾＾

次は、展開公式を利用した応用問題？というか計算ミスが起こりやすそうな問題を取り上げていきます。

スポンサーリンク

分数が出てくる展開

展開の計算において、分数が含まれているモノは計算ミスが多発します。

その為、ここでは分数の展開をひたすら練習していきましょう！

計算方法が変わるわけではありませんので、分数の計算をしっかりと身につけれもらえれば解くことができるはずです。がんばろー！

 

まずは、こちら

$$\large{\left(x+\frac{1}{2}\right)^2}$$

分数が出てきても、ちゃんと公式に当てはめていけばOKです。

$$\left(x+\frac{1}{2}\right)^2$$

$$=x^2+2\times x\times \frac{1}{2}+\left(\frac{1}{2}\right)^2$$

$$=x^2+x+\frac{1}{4}$$

 

次はこちらの展開です。

$$\large{\left(\frac{2}{3}x+\frac{1}{4}y\right)\left(\frac{2}{3}x-\frac{1}{4}y\right)}$$

うぉーー見た目が難しそうっすね(^^;

でも、乗法公式②に当てはめていけば楽勝です。

$$\left(\frac{2}{3}x+\frac{1}{4}y\right)\left(\frac{2}{3}x-\frac{1}{4}y\right)$$

$$=\left(\frac{2}{3}x\right)^2-\left(\frac{1}{4}y\right)^2$$

$$=\frac{4}{9}x^2-\frac{1}{16}y^2$$

 

最後はこちら

$$\large{\left(x+\frac{1}{2}\right)\left(x+\frac{1}{3}\right)}$$

こちらは乗法公式①を利用して解いていきましょう。

$$\left(x+\frac{1}{2}\right)\left(x+\frac{1}{3}\right)$$

$$=x^2+\left(\frac{1}{2}+\frac{1}{3}\right)x+\frac{1}{2}\times \frac{1}{3}$$

$$=x^2+\left(\frac{3}{6}+\frac{2}{6}\right)x+\frac{1}{6}$$

$$=x^2+\frac{5}{6}x+\frac{1}{6}$$

途中で通分が必要になるのが少し面倒ではありますが、解き方の考え方は同じですね^^

 

このように分数の展開であっても、公式通りに当てはめていくだけで簡単に解くことができます。

見た目が難しそうだからって、手を付けずに空白にしておくのは勿体ないですよ(^^)

置き換えをして工夫して展開する

次は、応用問題である置き換えを利用した展開計算について解説していきます。

$$\large{(x-y+2)(x-y-4)}$$

それぞれのかっこの中に同じようなかたまりがあるとき

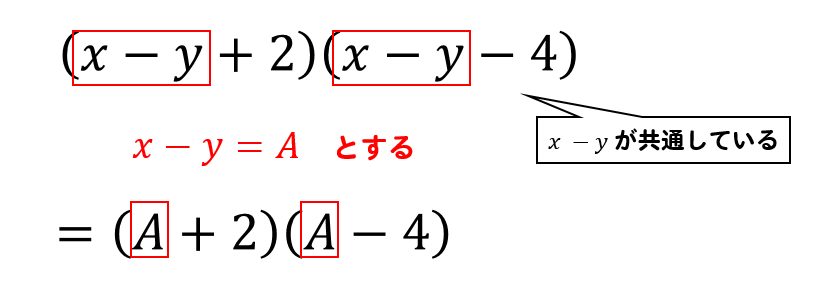
このように置き換えを利用してやると、少しラクに展開を計算することができます。

$$(A+2)(A-4)$$

$$=A^2-2A-8$$

ここから\(A=x-y\)を元に戻してやります。

$$=(x-y)^2-2(x-y)-8$$

$$=x^2-2xy+y^2-2x+2y-8$$

これで完成です！

 

普通に分配法則を使って計算しても良いのですが、それだとかなり面倒ですよね(^^;

そういうときには、今回のような置き換えを利用してやるとラクに計算できる場合もあります。

 

まとめ

お疲れ様でした！

最後に乗法公式を確認しておきましょう。

 

スポンサーリンク

効率よく学習を進めていきたい方は必見！

この記事を通して、学習していただいた方の中には


もっといろんな単元の学習を進めていきたい！

という素晴らしい学習意欲を持っておられる方もいる事でしょう。

だけど

どこの単元を学習すればよいのだろうか。

何を使って学習すればよいのだろうか。

勉強を頑張りたいけど 何をしたらよいか悩んでしまって

手が止まってしまう…

そんなお悩みをお持ちの方もおられるのではないでしょうか。

そんなあなたには

スタディサプリを使うことをおススメします。

スタディサプリを使うことで

どの単元を学習すればよいのか 何を解けばよいのか

そういった悩みを全て解決することができます。

スタディサプリでは学習レベルに合わせて授業を進めることが出来るほか、たくさんの問題演習も行えるようになっています。

スタディサプリが提供するカリキュラム通りに学習を進めていくことで

何をしたらよいのか分からない…

といったムダな悩みに時間を割くことなく

ひたすら学習に打ち込むことができるようになります(^^)

また、スタディサプリにはこのようなたくさんのメリットがあります。

スタディサプリを活用することによって

今までの悩みを解決し、効率よく学習を進めていきましょう。

「最近、成績が上がってきてるけど塾でも通い始めたの？」

「どんなテキスト使ってるのか教えて！」

「勉強教えてーー！！」

スタディサプリを活用することで どんどん成績が上がり

友達から羨ましがられることでしょう(^^)

今まで通りの学習方法に不満のない方は、スタディサプリを使わなくても良いのですが

学習の成果を高めて、効率よく成績を上げていきたい方

是非、スタディサプリを活用してみてください。

スタディサプリでは、14日間の無料体験を受けることができます。

まずは無料体験受講をしてみましょう！

⇓　　⇓　　⇓　　⇓　　⇓　　⇓　　⇓

スタディサプリ小・中学講座

スタディサプリ高校講座