【相似】平行線と比の利用、辺の長さを求める方法をまとめて問題解説！

今回は、中3で学習する

『相似な図形』の単元の中から

平行線と線分の比という内容について解説してきます。

ここでは、相似な図形の性質をつかって

いろんな図形の辺の長さを求めていきます。

長々と解説をするよりも

問題を見ながら、実践を通して学習するのが良いので

いろんな問題を解きながら解説をしていきます。

今回解説していく問題はこちら！

あの問題だけ知りたい！という方は

目次を利用して、必要な問題解説のところに飛んでくださいね

では、いきましょー！！

今回の記事はこちらの動画でも解説しています(/・ω・)/

初めに覚えておきたい性質

問題を解く前に、知っておいて欲しい性質があります。

それがこちら

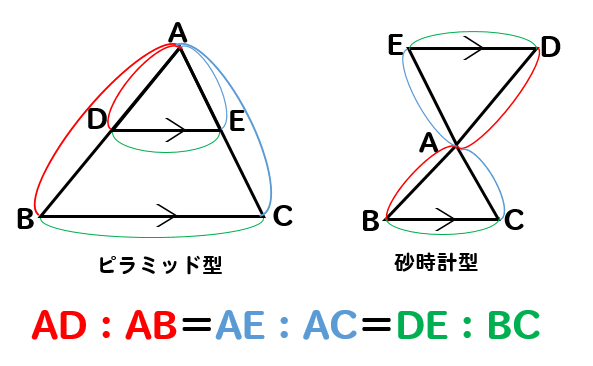
相似の性質を利用すると

このように、辺の長さの比をとってやることができます。

なんで？って思う方は

三角形をこうやってずらして考えると

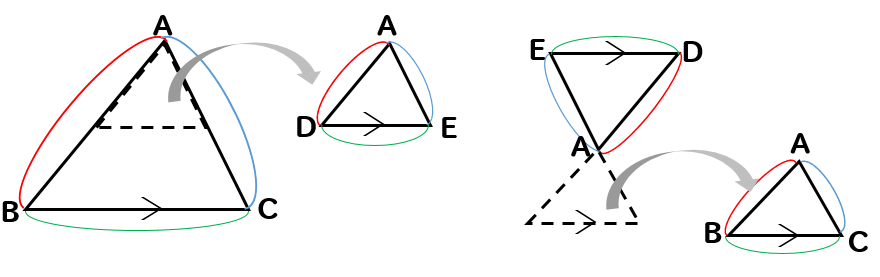
あー、対応する辺の比を取っているのか

と、気付いてもらえるのではないでしょうか。

それともう1つ

ピラミッド型の図形のときには、こういった比の取り方もできます。

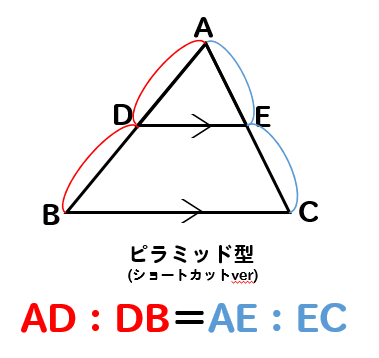
横どうしの辺を比べるときには

ショートカットができるんだなって覚えておいてください。

それでは、これらの性質を頭に入れて

問題に挑戦してみましょう。

平行線と線分の比 問題解説！

それでは（1）から（7）まで順に解説していきます。

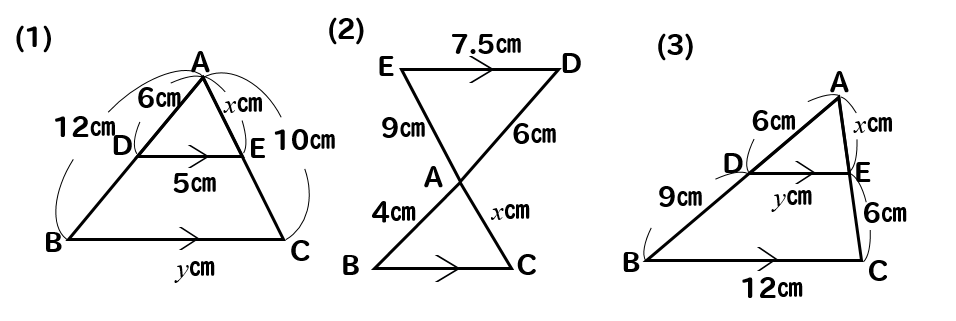
問題（1）解説！

\(x\)、\(y\)の値を求めなさい。

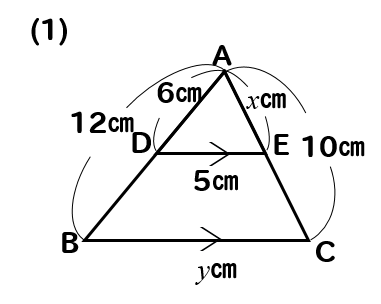
これはピラミッド型ですね。

小さい三角形と大きい三角形が隠れていて

それらの辺の長さを比で取ってやればいいです。

AD：AB＝AE：ACに当てはめて計算してやると

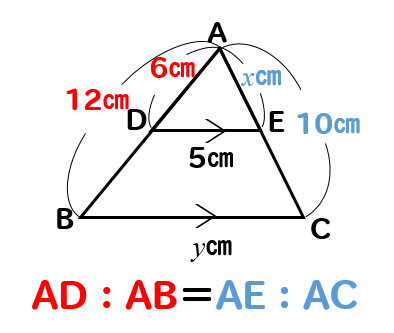
$$6:12=x:10$$

$$12x=60$$

$$x=5$$

次は

AD：AB＝DE：BCに当てはめて計算してやると

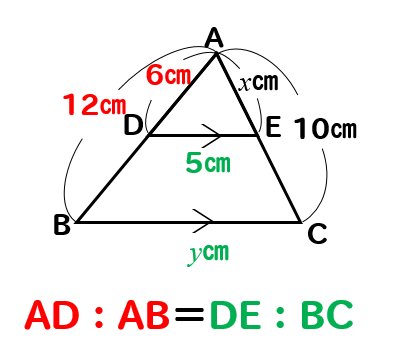
$$6:12=5:y$$

$$6y=60$$

$$y=10$$

問題（2）解説！

\(x\)、\(y\)の値を求めなさい。

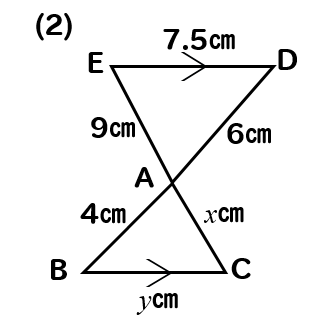
これは砂時計型ですね。

2つの三角形の対応する辺どうしを比でとってやります。

AD：AB＝AE：ACに当てはめて計算すると

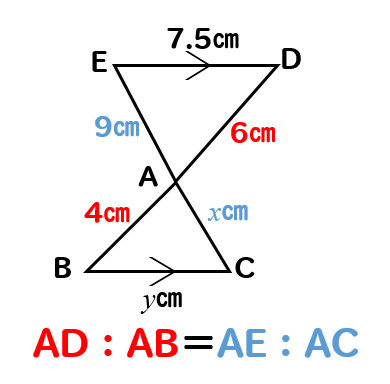
$$6:4=9:x$$

$$6x=36$$

$$x=6$$

次は

AD：AB＝DE：BCに当てはめて計算してやると

$$6:4=7.5:y$$

$$6y=30$$

$$y=5$$

問題（3）解説！

\(x\)、\(y\)の値を求めなさい。

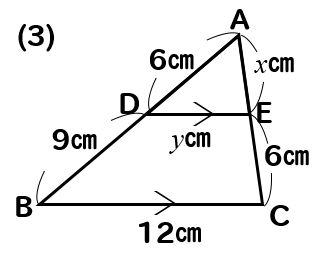
\(x\)を求めるときには

ピラミッド型のショートカットverを使うと少し計算が楽になります。

AD：DB＝AE：ECに当てはめて計算してみると

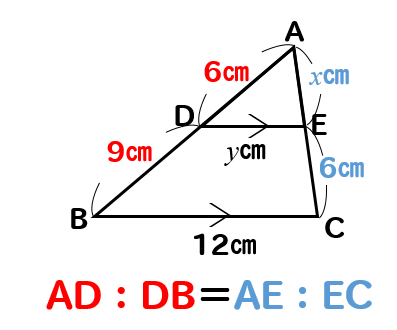
$$6:9=x:6$$

$$9x=36$$

$$x=4$$

次は\(y\)の値を求めたいのですが

下の長さを比べるときにはショートカットverは使えません！

なので、小さい三角形と大きい三角形の辺の比で取ってやりましょう。

AD：AB＝DE：BCに当てはめて計算してやると

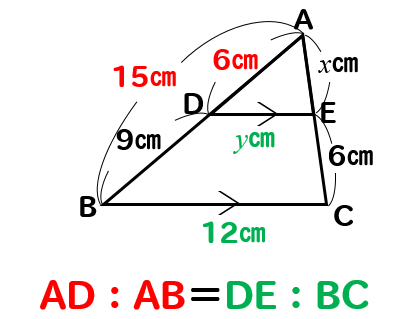
$$6:15=y:12$$

$$15y=72$$

$$y=\frac{72}{15}=\frac{24}{5}$$

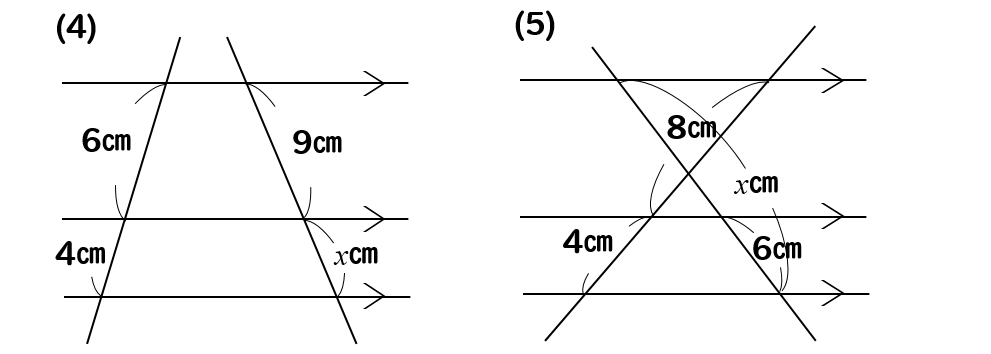
問題（4）解説！

\(x\)の値を求めなさい。

あれ？

相似な三角形がどこにもないけど！？

こういう場合には、線をずらして三角形を作ってやりましょう！

そうすれば、ピラミッド型ショートカットverの三角形が見つかります。

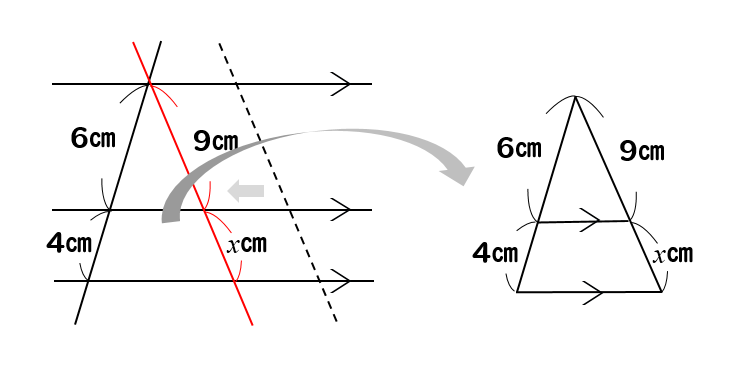
この三角形から比をとってやると

$$6:4=9:x$$

$$6x=36$$

$$x=6$$

三角形が見つからなければ、ずらせばいいですね！

問題（5）解説！

\(x\)の値を求めなさい。

なんか…

線が複雑でワケわからん！

こういう場合も線を動かして、わかりやすい形に変えてやります。

上の横線で交差するように線をスライドさせていくと

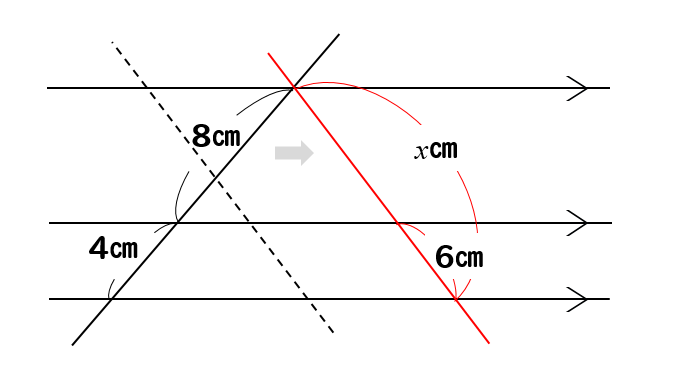
すると、ピラミッド型の図形を見つけることができます。

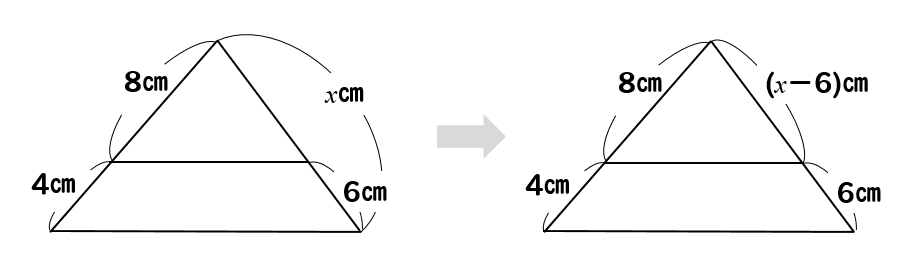
ピラミッドのショートカットverで考えていきましょう。

$$8:4=(x-6):6$$

$$4(x-6)=48$$

$$x-6=12$$

$$x=18$$

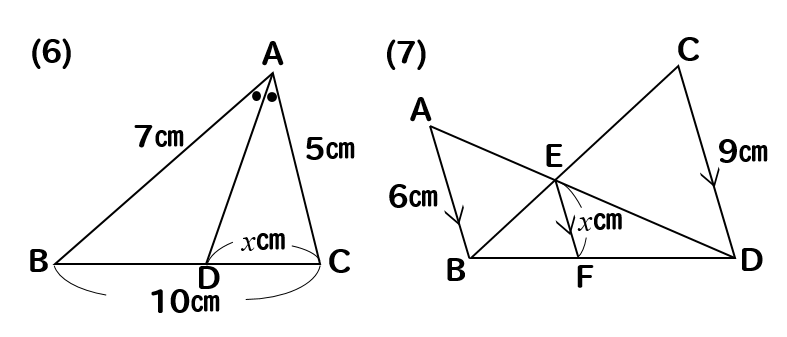
問題（6）解説！

ADが∠Aの二等分線であるとき、\(x\)の値を求めなさい。

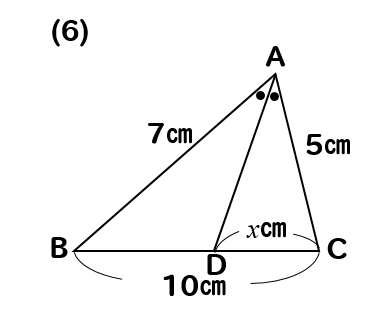
この問題を解くためには知っておくべき性質があります。

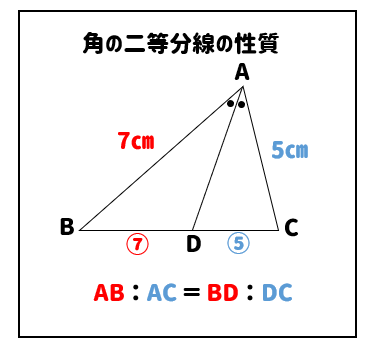
三角形の角を二等分線したときに、このような比がとれるという性質があります。

今回の問題はこれを利用して解いていきます。

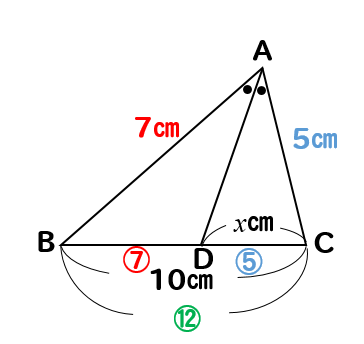
角の二等分の性質より

BD：DC＝7：5となります。

BDが7、DCが5なのでBCは2つを合わせた12と考えることができます。

よって、BC：DC＝12：5となります。

この比を利用してやると

$$12:5=10:x$$

$$12x=50$$

$$x=\frac{50}{12}=\frac{25}{6}$$

問題（7）解説！

\(x\)の値を求めなさい。

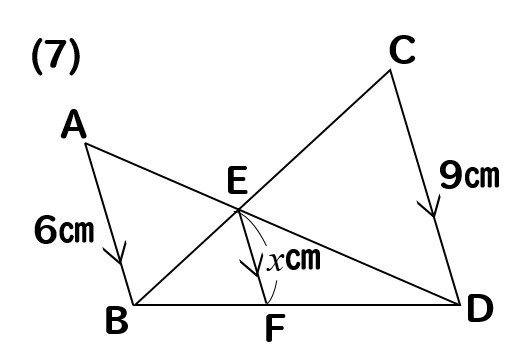
これは少し複雑ですね。

いくつかの相似な図形を辿りながら\(x\)を求めていきます。

まずは、長さが与えられているAB、CDを含む△ABEと△DCEに注目します。

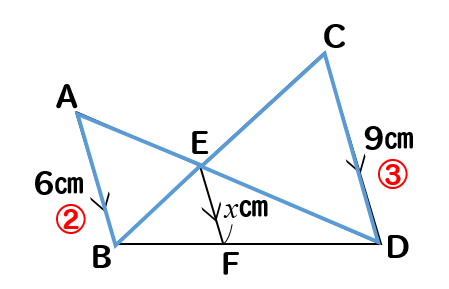
2つの図形は相似になっており

AB：CD＝6：9＝2：3より

相似比は2：3だと分かります。

つまり、他の辺の比も2：3になるので

AE：DE＝BE：CE＝2：3

とわかります。

このAE：DE＝2：3ということを利用して

次は、△ADBと△EDFに注目すると

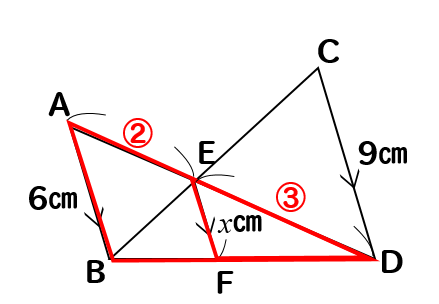
ピラミッド型が横にたおれた図形を見つけることができます。

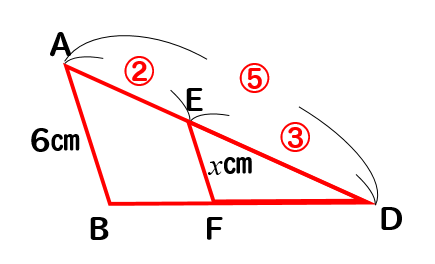
よって、この図形から辺の比をとってやると

DE：DA＝EF：ABより

$$3:5=x:6$$

$$5x=18$$

$$x=\frac{18}{5}$$

この問題では、2組の相似な図形に注目して

比を辿ってやりながらxを求めます。

この問題に関しては

実はラクに求める裏ワザ公式もあります。

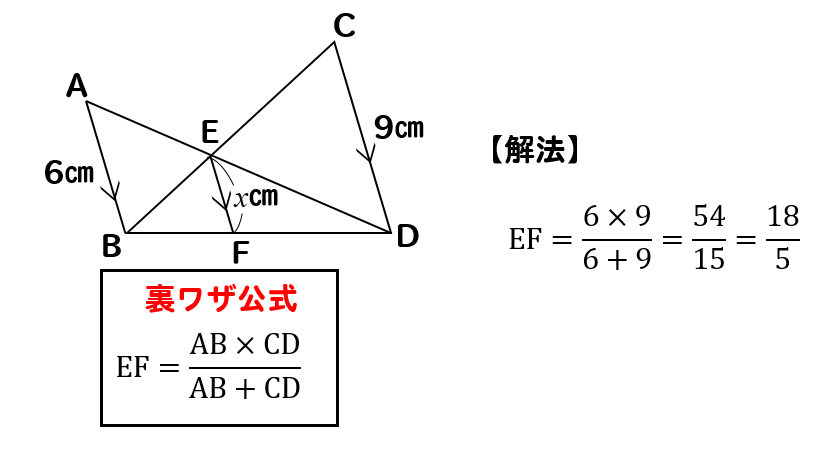
しかし、裏ワザ公式に頼ってしまうと

応用問題が出されたときに

対応しきれない部分もあるので

できるだけ、比を辿っていく方法で覚えておいて欲しいです。

裏ワザ公式は、答えがあっているかの確認などで

利用してもらえれば効果バツグンなはずです(^^)

平行線と線分の比　まとめ

以上、7パターンの問題について解説してきました。

おそらくこれらのパターンをしっかりと理解できていれば

ほとんどの問題には対応できるのではないかと思います。

比の取り方は、練習で身につけていくのが一番です。

間違ってもいいから、とにかく練習あるのみ！

困ったときはこの記事の解説を振り返って参考にしてみてくださいね(^^)

ファイトだー！

次は更なる応用問題にも挑戦だ！

【中3相似】中点連結定理、三等分の三角形求め方を問題解説！

【相似】平行四辺形と面積比の問題を徹底解説！