今回の記事では、中学数学で学習する
「二点間の距離の求め方」
について、イチから解説していきます。
結論から言ってしまうと
このような公式を使うことで
簡単に求めることができます。
では、どのような考え方で距離を求めればよいのか。
そして、公式の使い方は？？
イチから確認していきましょう！
ちなみに、今回の記事では「三平方の定理」を活用します。
なにそれ？という方はまずこちらの記事を読んでみてね！
二点間の距離の求め方
【問題】
2点 \(A(-1,2)\)と \(B(3,5)\)間の距離を求めなさい。
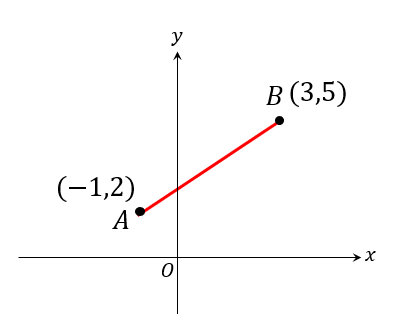
斜めの長さなんて、どうやって求めるの…？
と思ってしまいますが、次のように直角三角形を作って求めることができます。
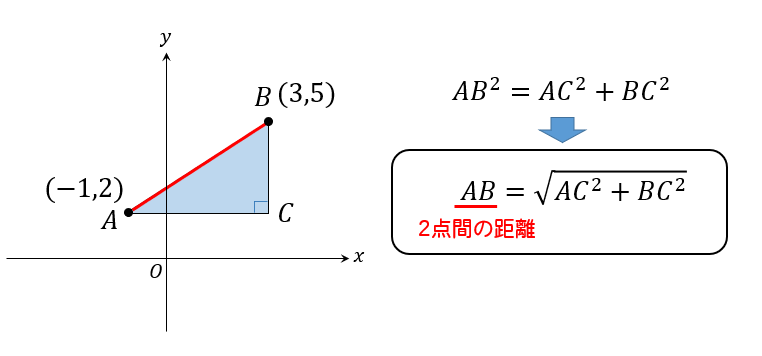
では、この考え方を利用して2点間の距離を求めてみましょう。
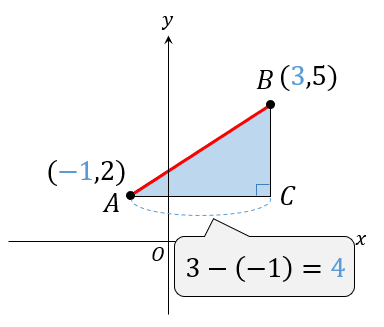
まずは\(AC\)の長さを求めます。
\(AC\)とは、ヨコの長さですからそれぞれの\(x\)座標に注目して、
（大きい値、右）ー（小さい値、左）
と計算してください。
次は\(BC\)の長さを求めます。
\(BC\)とは、タテの長さですからそれぞれの\(y\)座標に注目して、
（大きい値、上）ー（小さい値、下）
と計算してください。
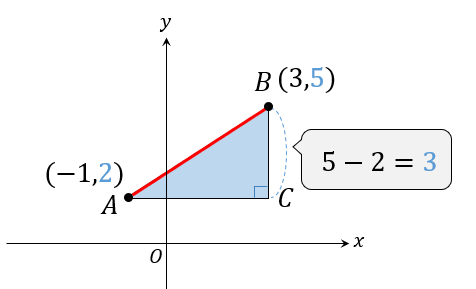
ここまで求まったら、あとは三平方の定理に当てはめていけばOKですね！
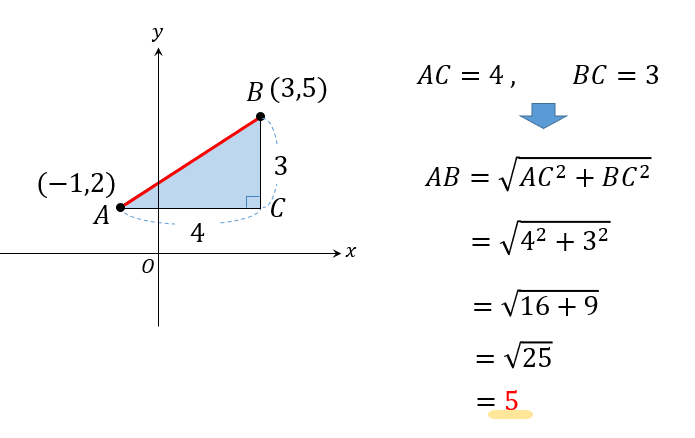
手順としてはこんな感じ！
- それぞれの\(x\)座標から、ヨコの長さを求める。
- それぞれの\(y\)座標から、タテの長さを求める。
- ①②を用いて三平方の定理に当てはめて計算する。
- 完成！
ちょっと、手順が多くてめんどうだなぁ…
と感じた方は次の公式を覚えて、使えるようにしておくと便利です。
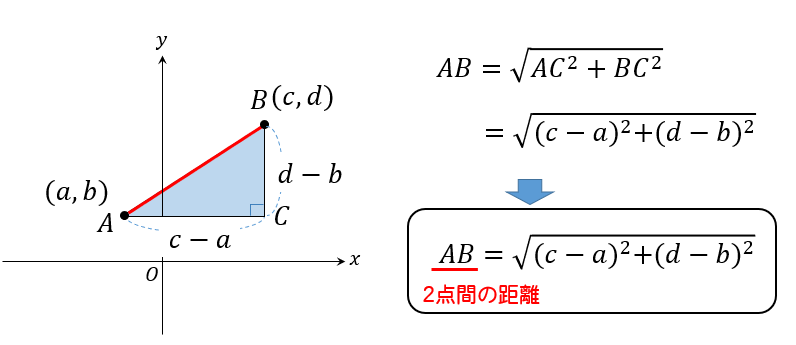
先ほどの問題を
この公式を使って解くとこんな感じになります。
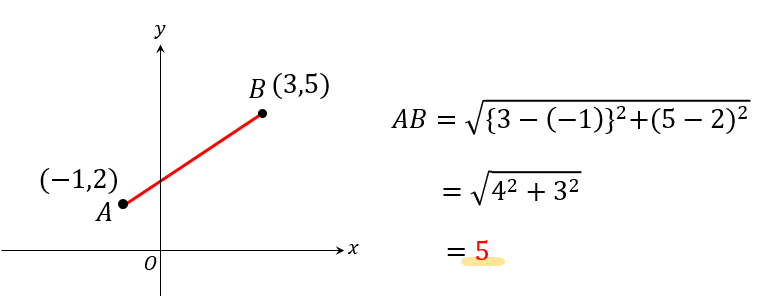
では、練習問題を解いて理解を深めておきましょう！
練習問題に挑戦！
【問題】
2点\(A(2,4)\)、\(B(5,3)\)の距離を求めなさい。
【問題】
2点\(A(-3,-1)\)、\(B(1,-5)\)の距離を求めなさい。
まとめ！
2点間の距離を求めたい場合には
直角三角形を作って、三平方の定理にあてはめて計算しましょう！
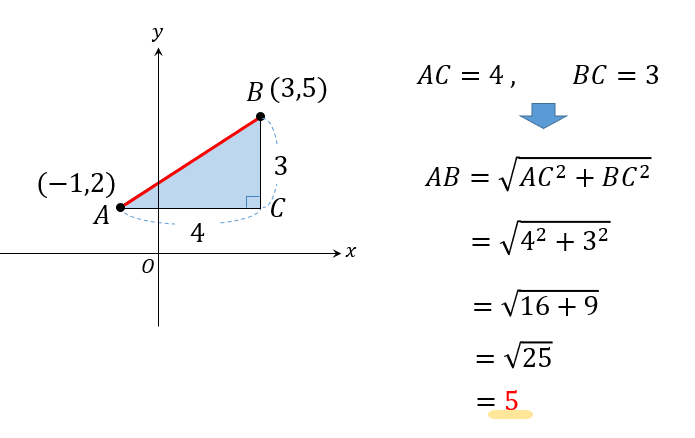
なるべく、手順を減らしたい！
という方は次の公式を使いこなせるよう練習しておいてくださいね(/・ω・)/
成績を上げて、志望校合格を勝ち取りたい中3生の方！
数スタの無料メルマガ講座で合格を勝ち取りませんか？
① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ わからないを解決！質問対応サポート
④ オリジナル教材の配布など、様々な企画を実施！
今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
[…] 二点間の距離の求め方をイチから解説！ […]