今回は高校数学Aで学習する
「円の接線と弦の作る角」
についてサクッと解説していきます。
円の接線と弦の作る角とは、
接弦定理とも呼ばれ、次のような定理のことです。
今回の内容はこちらの動画でも解説しています！
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします＾＾
接線と弦のつくる角の定理とは？
【接線と弦のつくる角の定理】
円の接線とその接点を通る弦のつくる角は、その角の内部にある弧に対する円周角に等しくなる。
うーん…説明だけを見ても
何を言っているのかサッパリ分かりませんね(^^;)
図を見ながらイチから解説していきますね。
まずは、円と接線があったとき
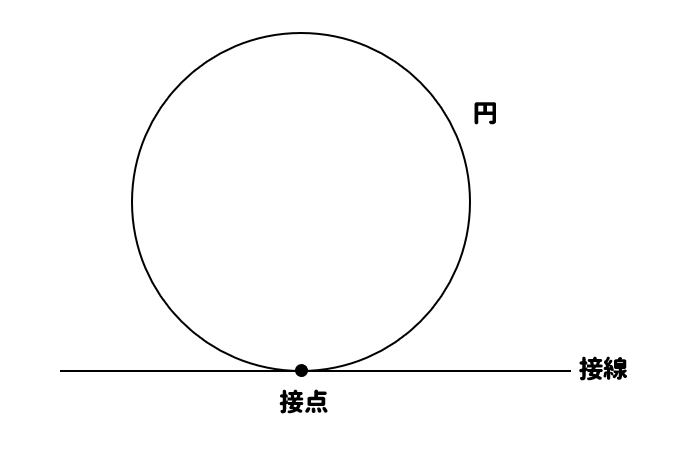
次に、接点を通る弦を引いてみます。
このとき、接線と弦のなす角ができますね。
この角を含む弧に対する円周角を考えます。
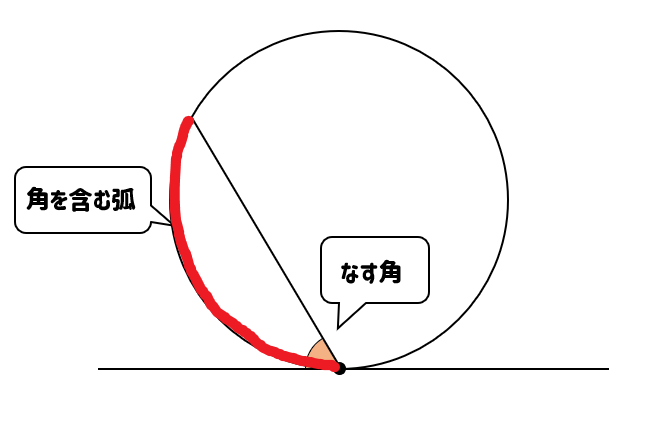
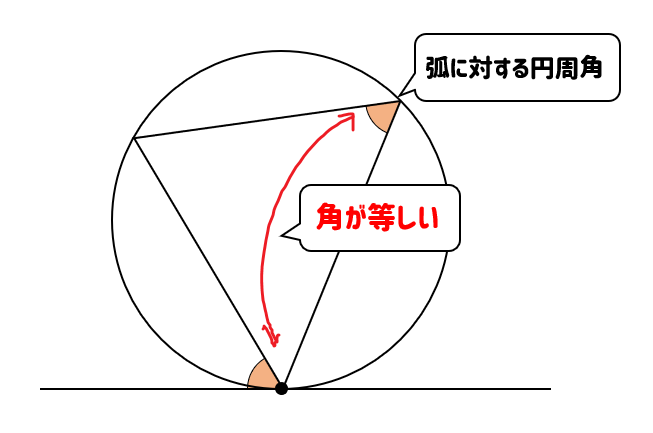
すると、この2つの角は同じ大きさになっているのです。
これが円の接線と弦のつくる角の定理です。
イメージとしては
接点にピタッと内接している三角形は
クロスする位置の角が同じだ！
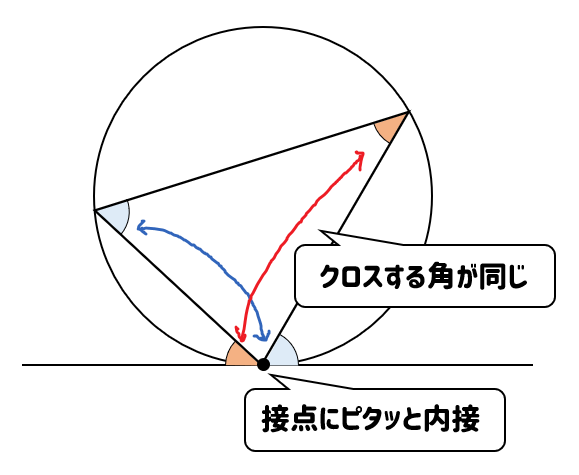
って感じで覚えてもらえるといいかと思います(^^)
接線と弦のつくる角の定理の証明
では、なぜこのような定理が成り立つのか。
簡単に確認しておきましょう！
なぜ、次のような位置にある角の大きさが等しくなるのでしょうか。
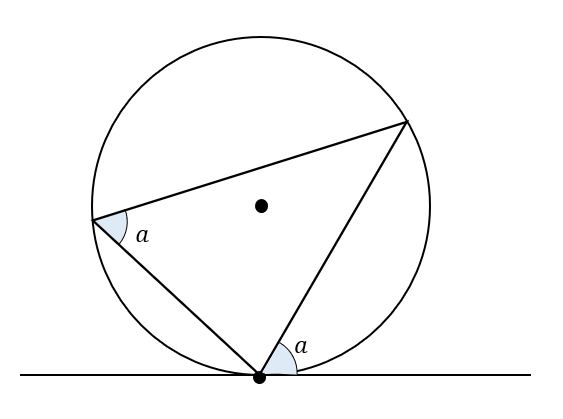
これを考えるには、まず
接点から、直径になるように線を引いて
下の図のような三角形を考えます。
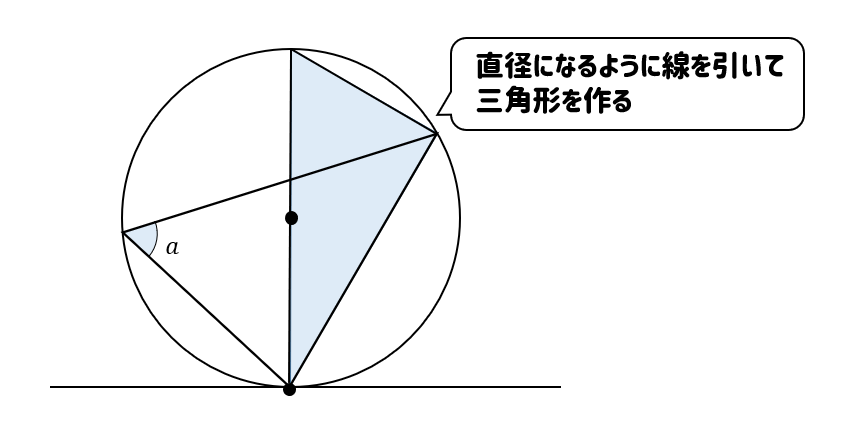
すると、次の図のように
90°の角、円周角の定理によって同じ大きさの角が見つかりますね。
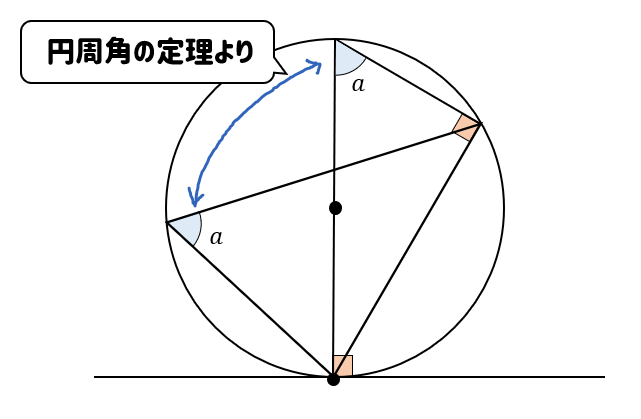
すると…
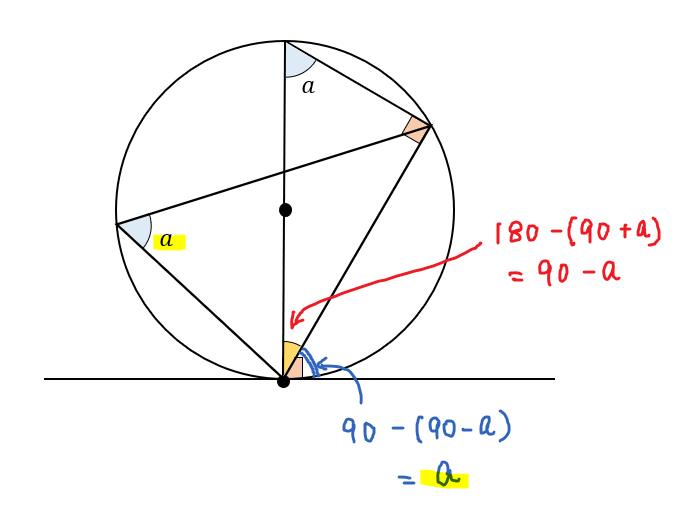
こんな感じで計算ができるので
クロスする位置にある角は同じ値になることが分かりましたね(^^)
接線と弦のつくる角【問題】
【問題】
次の図で、\(x\)の大きさを求めなさい。ただし、直線は円に接している。
【答え】
$$30°$$
クロスする位置が等しくなるでしたね！
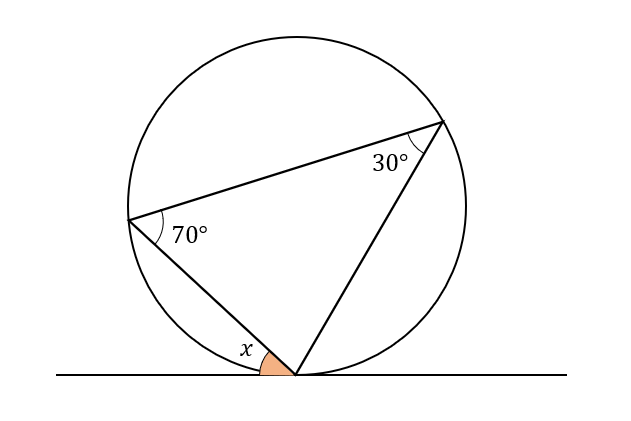
【問題】
次の図で、\(x\)の大きさを求めなさい。ただし、直線は円に接している。
【答え】
$$30°$$
このままでは定理が使えないので、補助線を引いてから考えましょう。
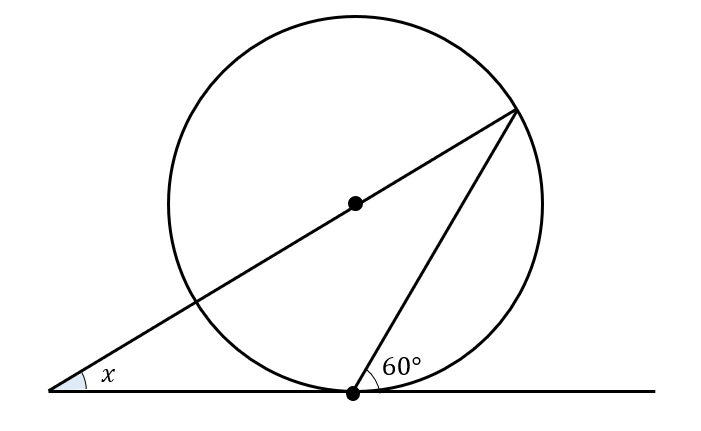
まとめ！
お疲れ様でした！
最後にもう1度、円の接線と弦のつくる角の定理を確認しておきましょう。
【接線と弦のつくる角の定理】
円の接線とその接点を通る弦のつくる角は、その角の内部にある弧に対する円周角に等しくなる。
うん、文で確認するとややこしすぎるｗ
なので、図でイメージできるようにしておけばOK。
クロスするとことが同じ！
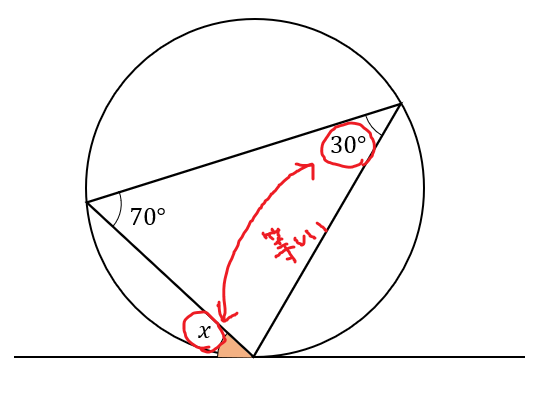
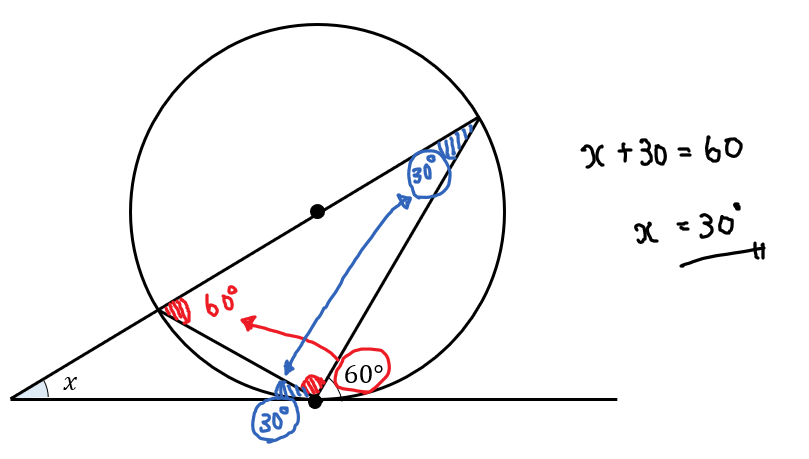
コメントを残す