今回は二等辺三角形の角度の求め方について解説していくよ！
よく出題される問題を取り上げて
解説をつけながら説明をしていくので
実際に問題を解きながら記事を読んでください(^^)
では、いくぞー！
今回の記事内容は、こちらの動画でも解説しています(/・ω・)/
Contents
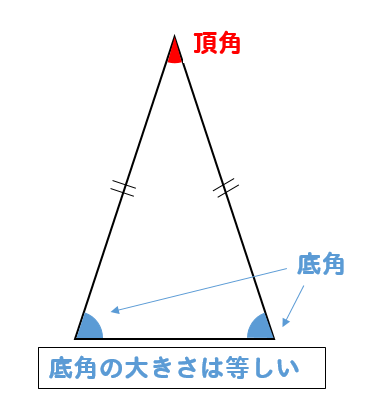
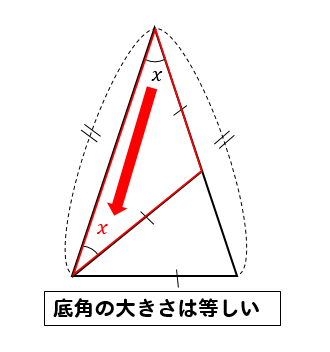
覚えておきたい二等辺三角形の性質
まず、角度の問題に挑戦する前に
知っておいてもらいたい二等辺三角形の性質があります。
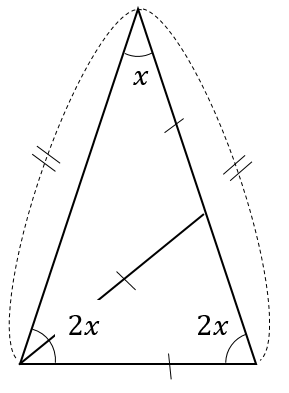
『二等辺三角形の底角は同じ大きさになる』
複雑な公式を覚えたりなど、必要ありません。
これを知っておけば角度の問題は大丈夫！
では、挑戦していきましょう。
厳選6パターンの問題に挑戦！
それでは、二等辺三角形の角度を求める問題をパターン別に解説していきます。
底角が与えられるパターン
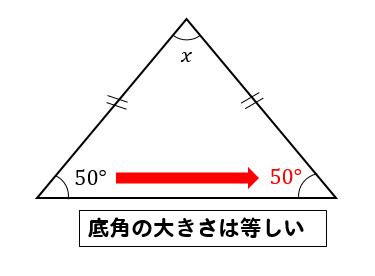
次の\(∠x\)の大きさを求めなさい。
答え
$$80°$$
50°の角は底角にあたるところですね。
二等辺三角形の性質より
底角の大きさは等しいので
底角は2つとも50°だということがわかります。
よって、三角形のすべての角を足すと180°になることから
$$x=180-(50+50)=80$$
となります。
底角は等しい！
これを覚えておけば解ける問題でした。
頂角が与えられるパターン
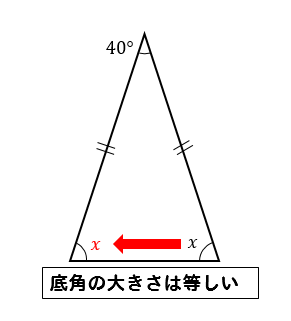
次の\(∠x\)の大きさを求めなさい。
答え
$$70°$$
頂角が与えられたときには
底角2つ分でいくらになるか？
を考えることが大切です。
今回の問題であれば
頂角が40°であることから
底角2つ分で\(180-40=140°\)だとわかります。
そして、底角は同じ大きさになるので
140°を２等分してやれば
底角１つ分の大きさを求めることができます。
$$140\div 2=70°$$
数学が得意な人は\(x\)を使って考えてもOKです。
底角は同じ大きさになるので
それぞれの角を\(x\)と表してやります。
そして、三角形の角をすべて足すと１８０°になることから
$$x+x+40=180$$
$$2x=180-40$$
$$2x=140$$
$$x=70$$
このように方程式を使って解ける人は
なかなか数学が得意な人ですね(^^)
外角が絡むパターン
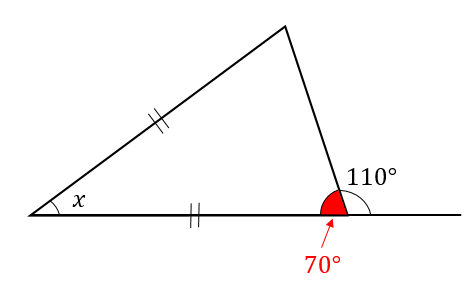
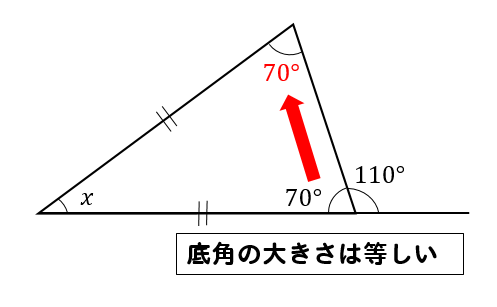
次の\(∠x\)の大きさを求めなさい。
答え
$$40°$$
二等辺三角形の外側の角度が与えられています。
この場合、二等辺三角形の中身の角度を求めていきます。
すると、今求めた70°という角は
二等辺三角形の底角なので
2つとも70°になるということがわかります。
よって、三角形の内角をすべて足したら180°になることから
$$x=180-(70+70)=40°$$
となります。
外角が与えられた場合には
そこをたどって、二等辺三角形の内角を求めていくと
答えに近づくことができますね(^^)
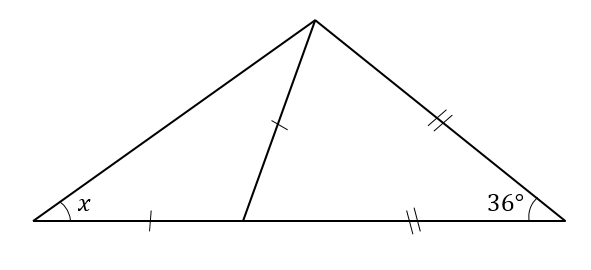
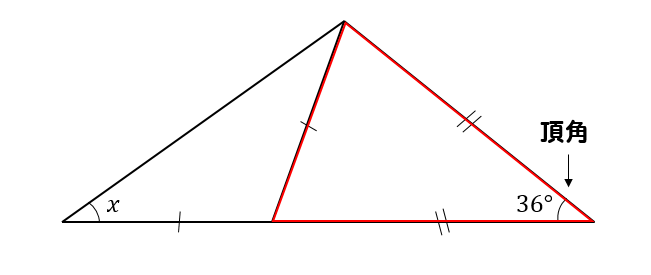
二等辺三角形が複数パターン
次の\(∠x\)の大きさを求めなさい。
答え
$$36°$$
二等辺三角形が2つくっついている問題ですね。
この場合、それぞれの二等辺三角形に注目して角度を１つずつ求めていきます。
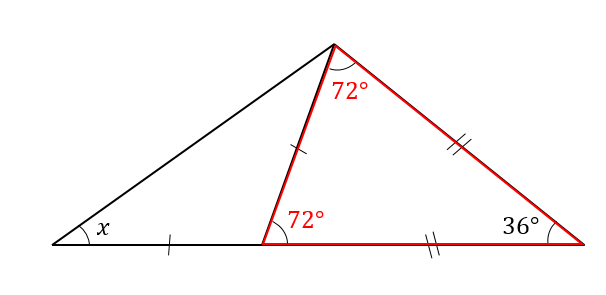
赤い二等辺三角形は、頂角が36°なので
底角1つ分の角は
$$180-36=144°$$
$$144\div 2 =72°$$
となります。
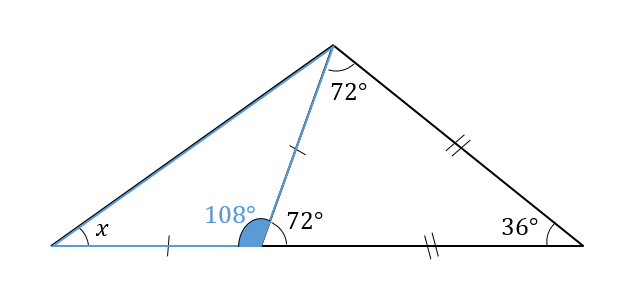
そこから、次は青い二等辺三角形に注目して\(x\)を求めていきます。
頂角が108°とわかっているので
底角1つ分(\(x\)の大きさ)は
$$180-108=72°$$
$$72\div 2 =36°$$
となりました。
二等辺三角形が複数くっついている場合には
それぞれの二等辺三角形において
1つずつ角度を求めていけば
答えに近づくことができますね。
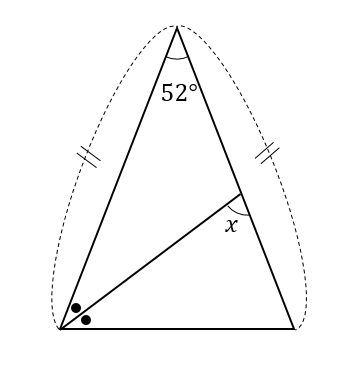
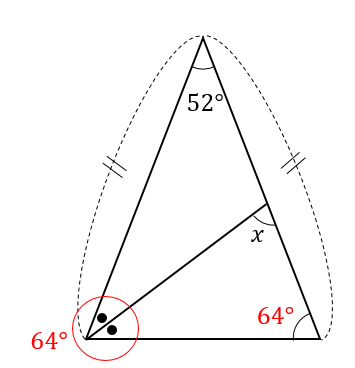
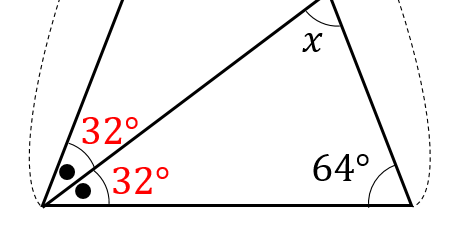
●が出てくるパターン
次の\(∠x\)の大きさを求めなさい。
答え
$$84°$$
●というのは、角の二等分を表すときによく使われますね。
●部分は同じ大きさだということを表しています。
まずは、二等辺三角形の底角1つ分の大きさを求めます。
$$180-52=128°$$
$$128\div 2=64°$$
すると●2個分で64°になるということがわかりますね。
そして、●1個分では
$$64\div 2=32°$$
ということがわかりました。
\(x\)を含む三角形に注目して
内角の和が180°になるということから
$$x=180-(32+64)=84°$$
となりました。
●が出てくる問題では
●1個分の大きさがいくらになるのかを求めてやることで
答えに近づくことができますね！
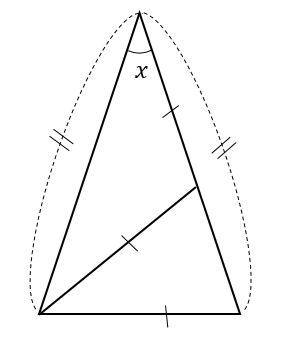
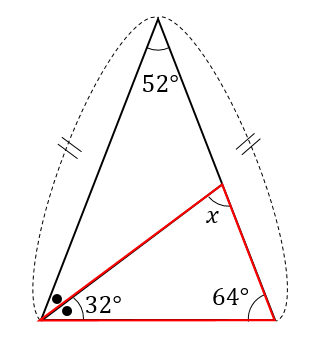
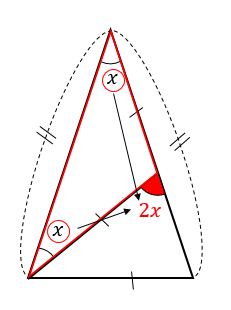
角度が何も書いていない！？パターン
次の\(∠x\)の大きさを求めなさい。
答え
$$36°$$
この問題では、どこにも角度が書いてありません。
どうやって\(x\)の大きさを求めていくのか。
まずは、角の大きさを\(x\)を使ってどんどん表していきます。
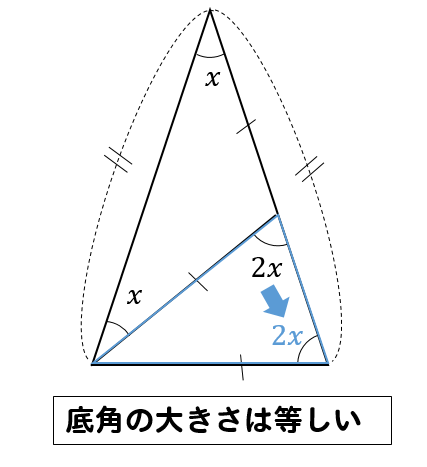
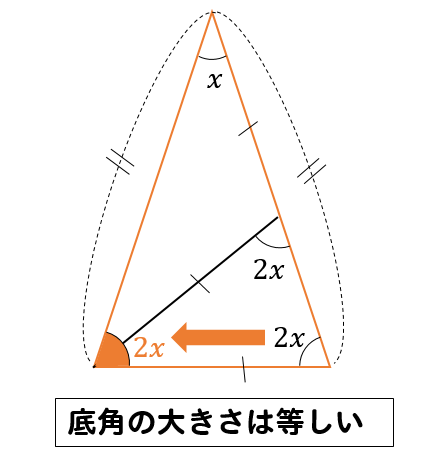
赤い二等辺三角形に注目して
外角の性質より
次は青い二等辺三角形に注目して
次は一番大きいオレンジの二等辺三角形に注目して
いろんな二等辺三角形をたどっていくことで
大きな二等辺三角形の角をこのように表すことができました。
すべての角を足すと180°になることから
$$x+2x+2x=180$$
$$5x=180$$
$$x=36°$$
となります。
どこにも角度が書いていないような問題では
二等辺三角形の性質を利用しながら
いろんな角を\(x\)を使って表すことで
答えに近づくことができます！
二等辺三角形の角度の求め方 まとめ
お疲れ様でした！
どの問題においても、使っている性質は
『底角の大きさは等しい』
というものだけですね。
二等辺三角形が見つかったら
どこが頂角で底角なのかをしっかりと把握することができれば
角度の問題は楽勝なはずです。
たくさんの問題演習を通して
理解を深めていきましょう！
ファイトだー(/・ω・)/
二等辺三角形をマスターしたら
次は正三角形ですね！
【証明の書き方】合同な三角形の証明問題の書き方を基礎から解説！
【直角三角形】証明問題の書き方とは？合同条件の使い方を徹底解説！
二等辺三角形の角度の求め方 厳選6問解説！←今回の記事
高校入試で使える公式集をプレゼント！
高校入試で使える公式をまとめた教材を作成しました！
定期テスト、入試で高得点を取るためには絶対に知っておきたいものばかりを集めています。
学校では教えてくれないような公式もありますよ(/・ω・)/
これは知らないと損をするかも…！？
無料の中学生メルマガ講座にご登録いただいた方に、
高校入試で使える公式集をプレゼントさせていただいております。
こちらから公式集を無料で手に入れちゃってください！
ご登録いただいたメールアドレスに教材を送らせていただきます。
登録は1分もあれば完了します。
ぜひ、こちらから中学生メルマガ講座に登録してみてくださいね(^^)
コメントを残す