難関高校の入試問題に挑戦!
難易度は『中』くらいです。
公立高校の入試を受験する方にとっても解けるようになっておきたい問題の1つです。
図形の知識も必要になってくるので
グラフと図形両方の復習になる良問です(^^)
それでは、どうぞ!
ちなみに難関関数の第1回はこちら
関数の入試問題~第2回~
問題
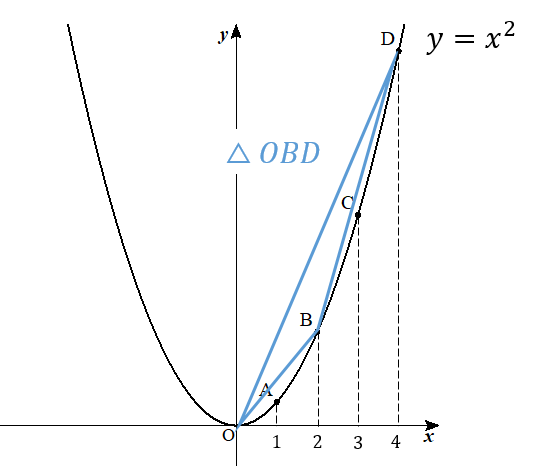
放物線\(y=x^2\)上に4点\(A,B,C,D\)があり、それらの\(x\)座標は順に\(1,2,3,4\)である。
このとき、(△OADの面積):(△OBDの面積):(△OCDの面積)を最も簡単な整数の比で表しなさい。
問題の考え方!
なんか文字や記号が多いから問題文が複雑に見えてしまいますね(^^;
何を聞かれているのか整理しておきましょう。
まず、放物線\(y=x^2\)があります。
その上に
\(x\)座標が\(1\)になるところをA
\(x\)座標が\(2\)になるところをB
\(x\)座標が\(3\)になるところをC
\(x\)座標が\(4\)になるところをD
となるようにそれぞれ点を取ります。


それぞれ点をとったら
△OAD、△OBD、△OCDの三角形に注目し



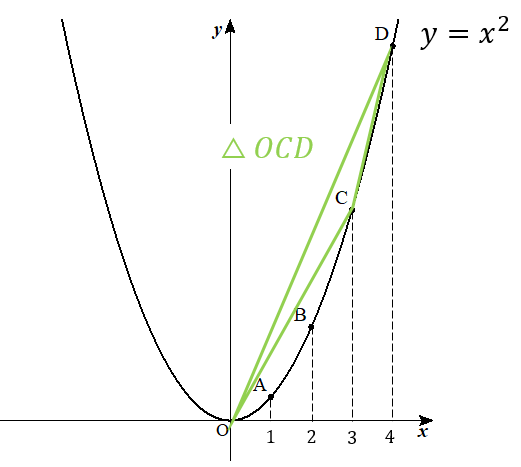

それぞれの面積の比を考える。
ということを問題で問われているのですね!
だから、それぞれの面積をどのように求めていくか。
これがポイントとなります。
問題の解答!
どの三角形も形が斜めになっていて
底辺と高さをとるのが難しいですね。
こういうときには
全体から削り取る!
という発想を持って面積を求めにいきましょう。
\(x\)軸の1,2,3,4の座標をそれぞれE,F,G,Hとして考えると
まず△OADの場合
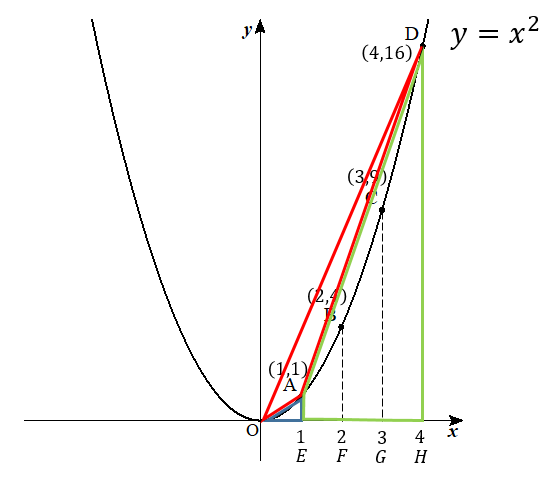

全体の△ODHから
△OAEと四角形AEHDを取り除いてやれば
△OADの面積を求めることができますね。
$$(△OAD)=(△ODH)-(△OAE)-(四角形AEHD)$$
それでは、まず△ODHの面積を求めてみましょう。
グラフの座標から長さを求めると
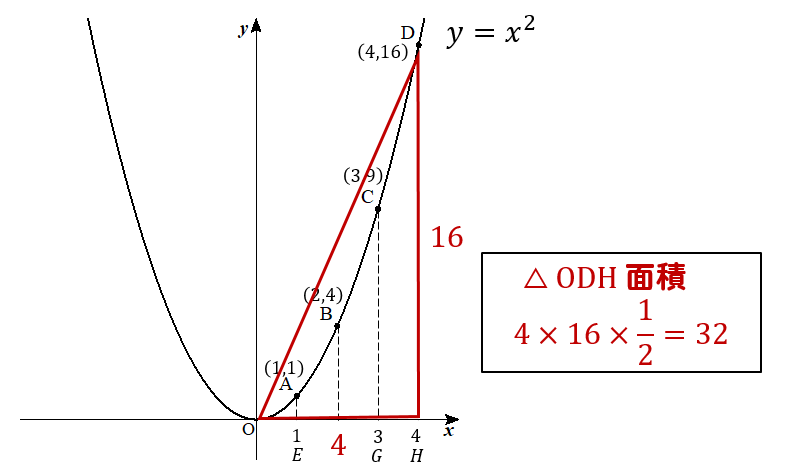

このように面積を求めることができます。
同様に、△OAEと四角形AEHDの面積を求めてみましょう。
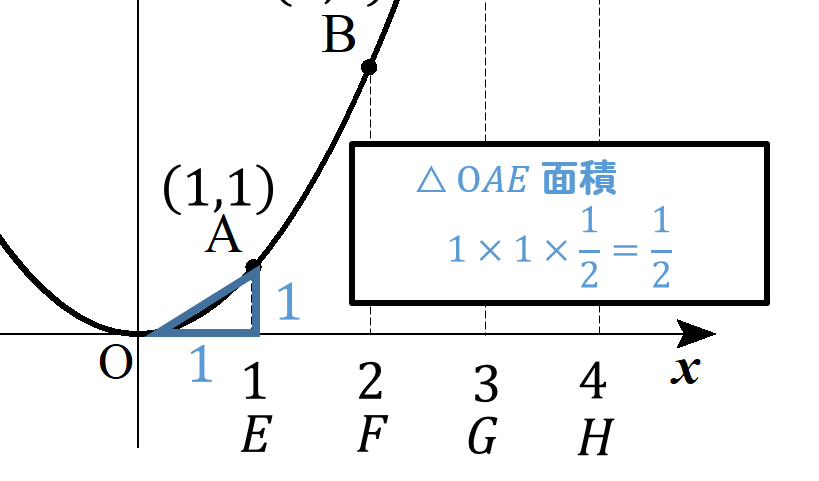

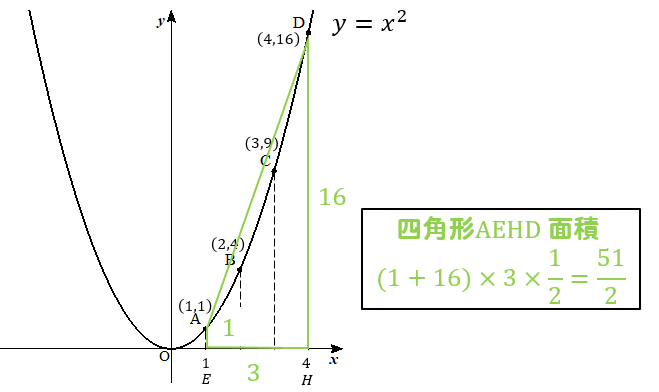

すると、それぞれこのように求めることができました。
よって
△OADの面積は
$$32-\frac{1}{2}-\frac{51}{2}=6$$
となりました。
これと同じように△OBDと△OCDを求めていきます。
$$(△OBD)=(△ODH)-(△OBF)-(四角形BFHD)$$
であることから
$$(△OBD)=32-4-20=8$$
$$(△OCD)=(△ODH)-(△OCG)-(四角形CGHD)$$
であることから
$$(△OCD)=32-\frac{27}{2}-\frac{25}{2}=6$$
これにより、それぞれの面積が求まったので面積比は
$$(△OAD):(△OBD):(△OCD)=6:8:6$$
$$=3:4:3$$
となりました。
答え
$$3:4:3$$
まとめ
お疲れ様でした!
グラフから面積を求める問題では、座標をしっかりと読み取ることが大事です。
座標が分かれば図形の長さが求めれるもんね(^^)
長さを求める問題についてはこちらでも解説しているので参考にしてみてください!
そして、底辺と高さが読み取りにくい場合には、今回のように全体から余分なものを削り取るという方法も頭に入れておいてください!
第2回は、以上(/・ω・)/



















コメントを残す