今回は『分母の有理化』について解説していくよ!
有理化っていうのは
ルートの計算をやっていく上で
すっごく大切な式変形になるから
この記事を通して、しっかりとマスターしていこう!
今回の記事はこちらの動画でも解説しています(/・ω・)/

分母の有理化ってなに??
分母にルートの数があるとき
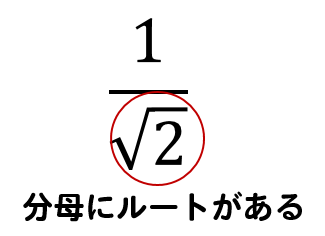
これにある式変形をすることで
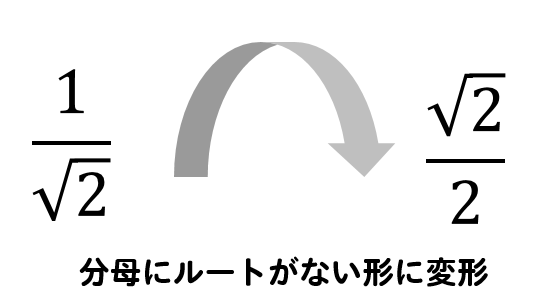
ルートをなくしてしまう
つまり、無理数を有理数に変形する
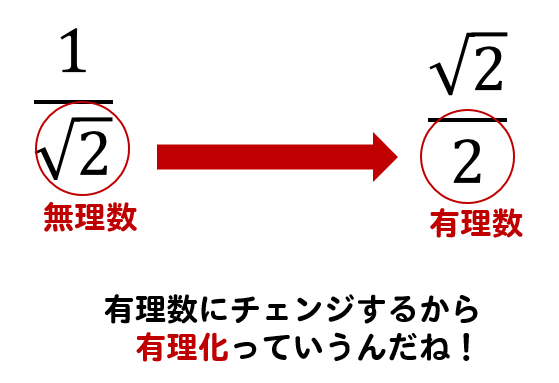
これを分母の有理化といいます。
それじゃぁ
どんな式変形をすれば、ルートを消すことができるのかというと
ここでルートの特徴を思い出してもらいたい。
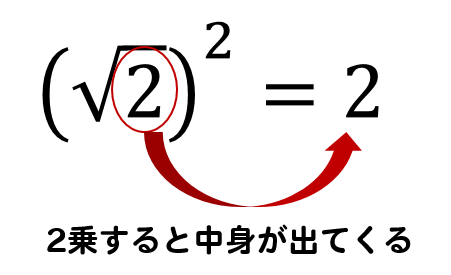
このようにルートは2乗すると
中身が出てくるんでしたね!
この性質を利用して
分母にあるルートを分母・分子の両方に掛けることで
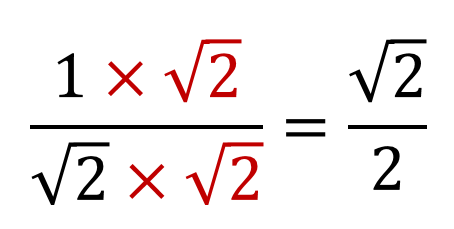
分母にあったルートをなくして、有理数に変形することができます。
なんで、分母と分子の両方に掛けないといけないかって??
それはね
分数の特徴を使っているんだよ!
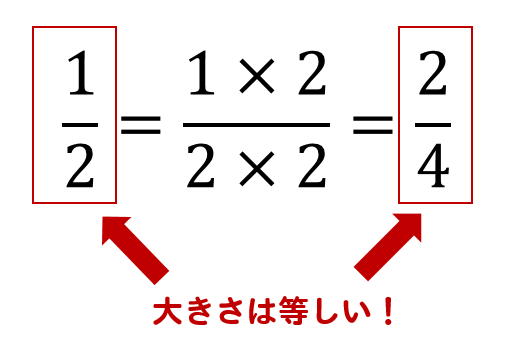
分数というのは、分母と分子の両方に同じ数を掛けるのであれば
大きさは変わらないという特徴があったよね!
だから、分母と分子の両方に同じルートを掛けることで
分数の大きさを変えることなく
見た目だけをチェンジすることができるってわけ!
$$\large{\frac{1}{\sqrt{2}}=\frac{1\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}=\frac{\sqrt{2}}{2}}$$

分母の有理化をやってみよう!
それでは、いくつかの例題を通して
分母の有理化の特徴を身につけていきましょう!
例題1
次の数を変形して、分母にルートがない形にしなさい。
$$\Large{\frac{6}{\sqrt{3}}}$$
この分数を有理化したい場合
分母にある\(\sqrt{3}\)を分母と分子の両方に掛けていきましょう。
$$\Large{\frac{6}{\sqrt{3}}=\frac{6\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}}$$
$$\Large{=\frac{6\sqrt{3}}{3}}$$
よしゃー!できたーっ!
と、油断しないでください。
ちゃんと約分もしてやって
$$\Large{=2\sqrt{3}}$$
ここまで持っていきましょう。
分母の有理化をすると、約分が出来る場合も多いので
最後まで油断しないようにね!
例題2
次の数を変形して、分母にルートがない形にしなさい。
$$\Large{\frac{4}{\sqrt{12}}}$$
この分数を有理化する場合には
\(\sqrt{12}\)をそのまま掛けてしまってもいいのですが
$$\Large{\frac{4}{\sqrt{12}}=\frac{4}{2\sqrt{3}}}$$
$$\Large{=\frac{2}{\sqrt{3}}}$$
このように\(\sqrt{12}\)の中身を簡単にしてやることで
分数全体をスッキリとさせることができます。
分数をここまで変形してから、有理化をしていきましょう!
$$\Large{\frac{2}{\sqrt{3}}=\frac{2\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}}$$
$$\Large{=\frac{2\sqrt{3}}{3}}$$
例題3
次の数を変形して、分母にルートがない形にしなさい。
$$\Large{\frac{\sqrt{3}}{\sqrt{18}}}$$
こちらの分数も、分母のルートを簡単にできるので
まずはルートの中身を整理していきましょう。
$$\Large{\frac{\sqrt{3}}{\sqrt{18}}=\frac{\sqrt{3}}{3\sqrt{2}}}$$
ここから分母にある\(\sqrt{2}\)を掛けて有理化をしていきます。
分母には3という数もありますが
有理化をするために、掛けるのはルートだけでOKです。
$$\Large{=\frac{\sqrt{3}\times \sqrt{2}}{3\sqrt{2}\times \sqrt{2}}}$$
$$\Large{=\frac{\sqrt{6}}{3\times 2}}$$
$$\Large{=\frac{\sqrt{6}}{6}}$$
例題4
次の数を変形して、分母にルートがない形にしなさい。
$$\Large{\frac{\sqrt{3}+2}{\sqrt{2}}}$$
このように分子が多項式になっている場合でも
有理化のやり方は同じです!
分母にある\(\sqrt{2}\)を掛けて有理化をしていきましょう。
$$\Large{\frac{\sqrt{3}+2}{\sqrt{2}}}$$
$$\Large{=\frac{(\sqrt{3}+2)\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}}$$
分配法則を使って、\(\sqrt{2}\)を\(\sqrt{3}+2\)のそれぞれに掛けていきます。
$$\Large{=\frac{\sqrt{6}+2\sqrt{2}}{2}}$$
これで完成!
分母に2つの項があるときの有理化
ここからは高校生で学習する範囲になってきますが
考え方はとてもシンプルなので、中学生の方もぜひ挑戦してみましょう!
$$\Large{\frac{1}{\sqrt{3}+2}}$$
このように分母に2つの項がある場合には
どのように有理化をしていけば良いのか考えていきましょう。
先ほどと同じように
分母にあるルートを掛けるという方法では
$$\Large{\frac{1\times \sqrt{3}}{(\sqrt{3}+2)\times \sqrt{3}}}$$
$$\Large{=\frac{\sqrt{3}}{3+2\sqrt{3}}}$$
あれ…分母にルートが残っちゃいますね。
ということで、分母に2つの項があるときには
別の方法で有理化をしていく必要があります。
ここで、役に立つのが
乗法公式である次の式です。
$$\LARGE{(a+b)(a-b)=a^2-b^2}$$
\(\sqrt{3}+2\)に対して、2の符号を変えた\(\sqrt{3}-2\)を掛けることで
$$\Large{(\sqrt{3}+2)(\sqrt{3}-2)}$$
$$\Large{=(\sqrt{3})^2-2^2}$$
$$\Large{=3-4}$$
$$\Large{=-1}$$
このように2つの項からルートを消すことに成功しました。
ということで、これを利用して有理化をしていきます。
$$\Large{\frac{1}{\sqrt{3}+2}}$$
$$\Large{=\frac{1\times (\sqrt{3}-2)}{(\sqrt{3}+2)(\sqrt{3}-2)}}$$
$$\Large{=\frac{\sqrt{3}-2}{3-4}}$$
$$\Large{=\frac{\sqrt{3}-2}{-1}}$$
$$\Large{=-\sqrt{3}+2}$$
$$\large{\frac{c}{\sqrt{a}+b}=\frac{c\times (\sqrt{a}-b)}{(\sqrt{a}+b)(\sqrt{a}-b)}}$$
このように分母の多項式が
$$\large{(a+b)(a-b)=a^2-b^2}$$
の関係になるように、分母と分子に掛けて有理化をしていきます。
では、例題を通して理解を深めていきましょう!
例題1
$$\Large{\frac{2}{\sqrt{5}+\sqrt{3}}}$$
分母が両方ともルートの形になっていても考え方は同じです!
\(\sqrt{5}-\sqrt{3}\)を分母・分子に掛けて有理化をしていきます。
$$\Large{\frac{2\times (\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}}$$
$$\Large{=\frac{2(\sqrt{5}-\sqrt{3})}{5-3}}$$
$$\Large{=\frac{2(\sqrt{5}-\sqrt{3})}{2}}$$
$$\Large{=\sqrt{5}-\sqrt{3}}$$
これで分母に2つの項があっても
有理化はバッチリですね!!
それでは…
分母に3つの項があったらどうしますか!?
$$\LARGE{\frac{1}{\sqrt{2}+\sqrt{3}+\sqrt{5}}}$$
分母に3つの項があるときの有理化
分母に3つの項があるときの有理化は
先ほど紹介した2つのときと同じ考え方をします。
$$\Large{\sqrt{2}+\sqrt{3}+\sqrt{5}}$$
$$\Large{=(\sqrt{2}+\sqrt{3})+\sqrt{5}}$$
このように、3つあった項を
\((\sqrt{2}+\sqrt{3})\)と\(\sqrt{5}\)
というように項をくっつけて考えることで
2つの項にしていまいます。
よって、\((\sqrt{2}+\sqrt{3})-\sqrt{5}\)を掛けることで有理化をしていきます。
$$\frac{1\times\{(\sqrt{2}+\sqrt{3})-\sqrt{5}\}}{\{(\sqrt{2}+\sqrt{3})+\sqrt{5}\}\{(\sqrt{2}+\sqrt{3})-\sqrt{5}\}}$$
$$\large{=\frac{\sqrt{2}+\sqrt{3}-\sqrt{5}}{(\sqrt{2}+\sqrt{3})^2-(\sqrt{5})^2}}$$
$$\large{=\frac{\sqrt{2}+\sqrt{3}-\sqrt{5}}{2+2\sqrt{6}+3-5}}$$
$$\large{=\frac{\sqrt{2}+\sqrt{3}-\sqrt{5}}{2\sqrt{6}}}$$
ここまできたら、最初に練習した有理化を進めていきましょう。
$$\large{=\frac{(\sqrt{2}+\sqrt{3}-\sqrt{5})\times \sqrt{6}}{2\sqrt{6}\times \sqrt{6}}}$$
$$\large{=\frac{\sqrt{12}+\sqrt{18}-\sqrt{30}}{2\times 6}}$$
$$\large{=\frac{2\sqrt{3}+3\sqrt{2}-\sqrt{30}}{12}}$$
分母に3つの項があるときには
2つの項をくっつけて、全体を2つの項だと考えて有理化をしていきましょう。
【中学生向け】テストはこれでバッチリ!有理化の計算をマスターする演習プリント
お疲れ様でした^^
これで有理化のやり方は理解してもらえたと思います!
とはいえ、いろんな問題にチャレンジしてみると「ん、この場合はどうやるの?」「あれ?計算が上手くできないけど…」このように困ってしまう場面に出くわすこともあるでしょう。
そこで今回は「よーくミスが起こる有理化10選」ということで、基本からちょっとひねったものまで、テストに出てくる有理化計算を10題分ピックアップしました。
これらを一通りやってもらうことで、有理化計算はパーフェクトに仕上がるでしょう^^
ぜひ定期試験や模試対策として活用してみてください!
※今回は中学校で扱う計算のみをピックアップしています。
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
まとめ
お疲れ様でした!
これで分母の有理化はバッチリです(^^)
あとは、たくさん問題演習をこなして
理解を深めていきましょう!
分母の項が1つのとき
$$\large{\frac{b}{\sqrt{a}}=\frac{b\times \sqrt{a}}{\sqrt{a}\times \sqrt{a}}}$$
分母の項が2つのとき
$$\large{\frac{c}{\sqrt{a}+\sqrt{b}}}$$
$$\large{=\frac{c\times (\sqrt{a}-\sqrt{b})}{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}}$$
分母の項が3つのとき
$$\large{\frac{d}{\sqrt{a}+\sqrt{b}+\sqrt{c}}}$$
以上!
平方根の計算をマスターしたい方はこちらの記事もどうぞ!
>>>【平方根】ルートの計算方法まとめ!問題を使って徹底解説!
ルートとは?平方根の求め方を解説!分数や小数の場合はどうやる?
分母の有理化のやり方はこれでバッチリ!←今回の記事
【追記】分母の項が2つのとき、マイナスだったら?
このようなコメントをいただきましたので、例題を紹介しておきます。
次の数を変形して、分母にルートがない形にしなさい。
$$\Large{\frac{1}{\sqrt{3}-\sqrt{2}}}$$
分母に2つの項があるときには、1つの項の符号をチェンジしたものを掛ける!
というのがポイントです。
つまり、今回の\((\sqrt{3}-\sqrt{2})\) に対しては、\((\sqrt{3}+\sqrt{2})\) を掛けましょう。
$$\begin{eqnarray}&&\frac{1}{\sqrt{3}-\sqrt{2}}\\[5pt]&=&\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})} \\[5pt]&=&\frac{\sqrt{3}+\sqrt{2}}{3-2}\\[5pt]&=&\sqrt{3}+\sqrt{2}\end{eqnarray}$$
もしも、分母が…
\(\sqrt{5}-1\) だったら、\(\sqrt{5}+1\) を掛ける。
\(-\sqrt{5}-\sqrt{2}\) だったら、\(-\sqrt{5}+\sqrt{2}\) を掛ける。
こんな感じだね!
【追記】分母の項が3つあるとき、どこを1カタマリと考える?
といったコメントをいただいたので、こちらの3題を使って解説していきますね!

3つの項のうち、どこを1カタマリにするのか間違ってしまうと計算が上手く進まなくなります…汗
考え方としてはシンプルで(小)(中)(大)のうち、(小)(中)を1カタマリにする!と考えましょう。
なので、それぞれの問題では次のようにカタマリをつくって計算してください。


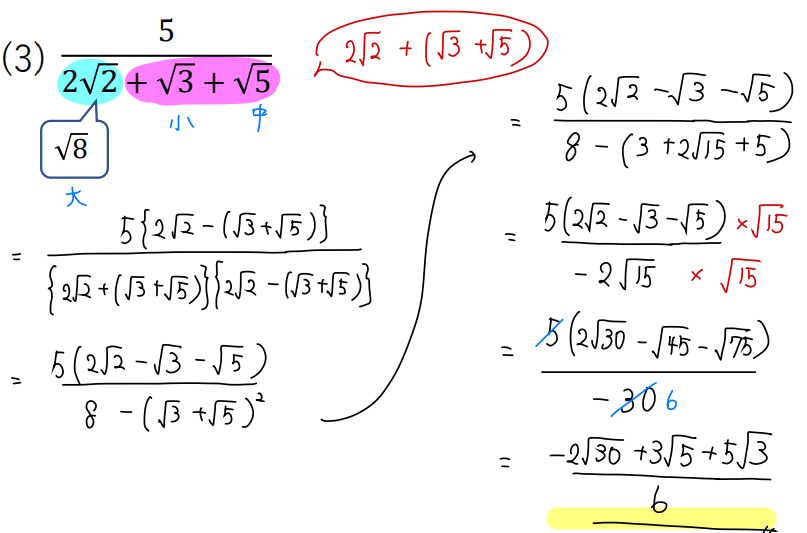
こうすることによって、計算がスムーズに進みますよね!
カタマリのとり方を間違えてしまうと計算が複雑になってしまい、
途中で「うわぁーーー!!」と投げ出したくなっちゃうので注意です(=_=)笑
詳しくはこちらの動画内でも解説しているので参考にしてみてください^^


















分母の項が2つのとき問題がマイナスだった場合どうすればいいですか?
コメントありがとうございます。
記事下に、追記としてお返事しております。
疑問は解決されましたでしょうか??
分母が複数の場合の乗法公式を利用した計算ですが、なぜ(a+b)(a-b)のようにわざわざマイナスを掛けるのでしょうか?公式だからと言ってしまえばそれまでですが……+を掛けても、-が+になるだけで数字は変わらないと思うのですが……反対にしなければいけないルールがあるのでしょうか?
(a+b)に対して符号をチェンジした
(a-b)をかけることにより
2乗ひく2乗の乗法公式が使えるので
上手くルートを消すことができます!
もしも
(a+b)に対して、
同じ(a+b)をかけてしまうと
(a+b)(a+b)=a^2+2ab+b^2
という形になってしまって
2abの部分にルートが残ってしまうんですね。
なので、
符号をチェンジしたものをかけて
有理化をしていくようになります^^
分母が3つある場合の有理化について質問させてください。
こちらのサイトでは3つある分母を次のような公式で表しています。
√a+√b+√c
={(√a+√b)+√c}{(√a+√b)-√c}
一方で、私が解いている分母が3つある場合の有理化では、次のような形で有理化されています
√a+√b+√c
={(√a+√c)+√b}{(√a+√c)-√b}
√bと√cの位置を入れ替えているのですが、何故このような方法なのか解説されていないので分かりません。
『2つの項をくっつけて、全体を2つの項だと考える』という点では共通しているのですが、
この2つの項とする場合、選ぶ項はどれでもいいのでしょうか?
※試しにこの記事にある分母3つの問題を、解説とは違うで紹介されている問題√2+√3+√5を
(√2+√3)+√5ではなく、√2+(√3+√5)として計算してみたところ解けなくなりました…
単純に計算ミスの可能性が高いのですが…
ご質問ありがとうございます!
分母に3つの項があるとき、
小、中、大のうち、小と中を1カタマリとおいて
計算をしていくようになります!
(そうすると計算がスムーズになるように問題設定されてるから)
記事の最後に追記として
解説を入れておいたので参考にしてもらえると嬉しいです!
早速のご回答ありがとうございます!
分母が3つある場合は項を小、中、大に分類して、小と中を1カタマリとしたほうが計算がスムーズになるからなんですね。
私が理解できなかった問題も「計算がスムーズになる」ことを重視して変形させていると考え、再度見直してみます。
記事への追記もありがとうございます!