今回は平行四辺形の角度、辺の長さの求め方について解説していくよ!
平行四辺形の性質を覚えておけば
簡単に解ける問題ばかりだから
今回の記事でしっかりとマスターしていこう!

今回の内容はこちらの動画でも解説しています^^
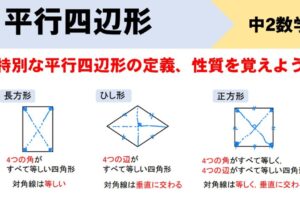
覚えておきたい平行四辺形の性質
平行四辺形の問題を解くために覚えておきたい4つの性質をまとめておきます。
2組の対辺はそれぞれ平行
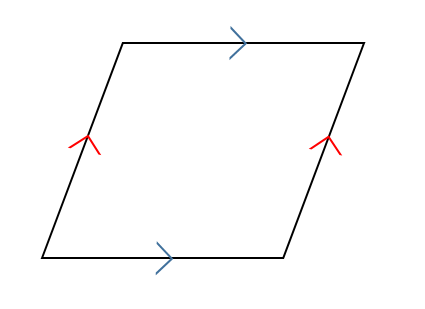
平行四辺形は向かい合う辺が、お互いに平行になっています。
平行になっているという性質を知っておくと
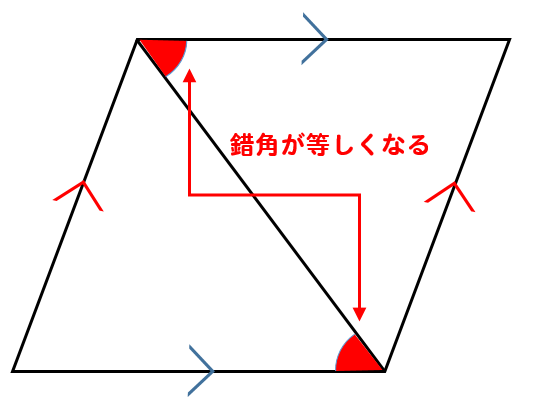
このように錯角が等しくなる
ということも利用できるようになりますね。
2組の対辺はそれぞれ等しい
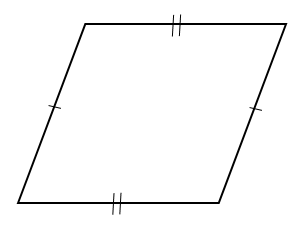
平行四辺形は、向かい合う辺がそれぞれ等しくなります。
2組の対角はそれぞれ等しい
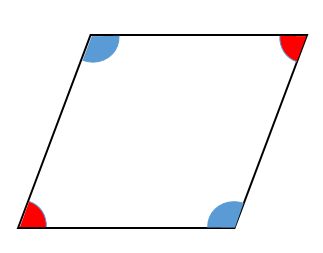
平行四辺形の向かいあう角は、それぞれ等しくなります。
ここで、もう一つ覚えておくと得なのが
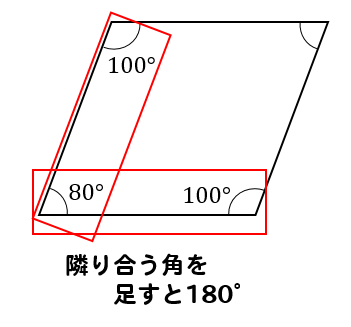
平行四辺形では、隣り合う角を足すと180°になる。
あとで問題に出てくるから覚えておいてね!
対角線はそれぞれの中点で交わる
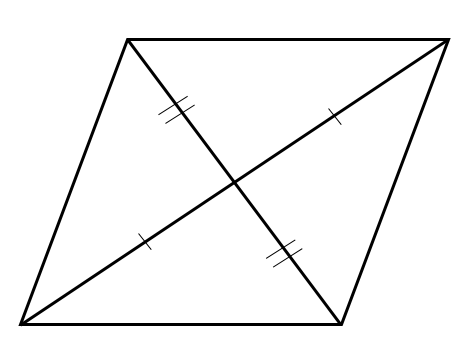
平行四辺形では、対角線を引くと
それぞれの中点で交わります。
厳選6パターンの問題に挑戦!
それでは、平行四辺形の角度、辺の長さを求める問題をパターン別に解説していきます。
対角、対辺の基本パターン
四角形ABCDが平行四辺形のとき、\(x,y\)の値を求めなさい。
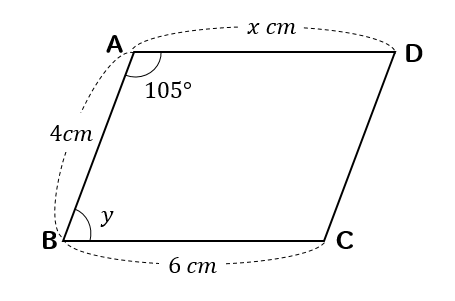
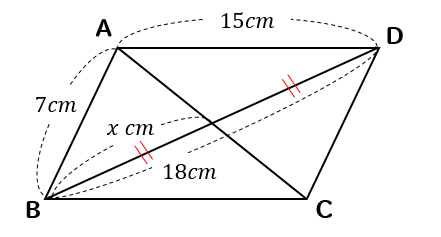
対角線を利用するパターン
四角形ABCDが平行四辺形のとき、\(x\)の値を求めなさい。

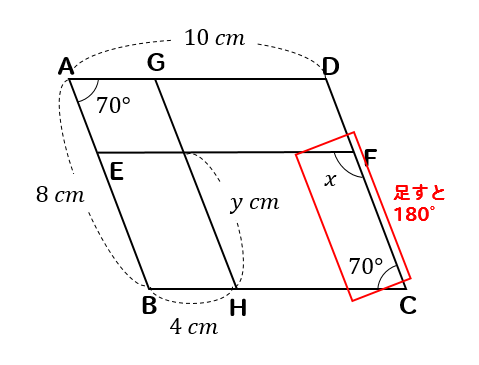
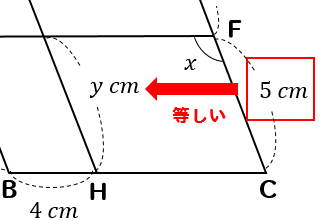
平行四辺形がたくさん!パターン
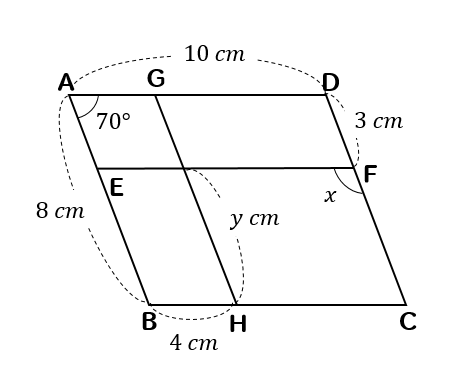
四角形ABCDが平行四辺形のとき、\(x,y\)の値を求めなさい。
ただし、AB//GH, AD//EFとする。

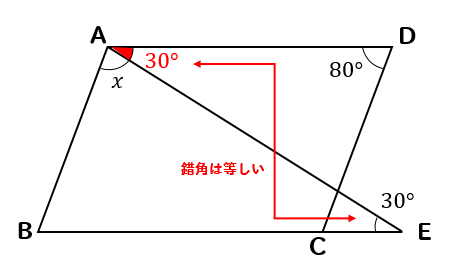
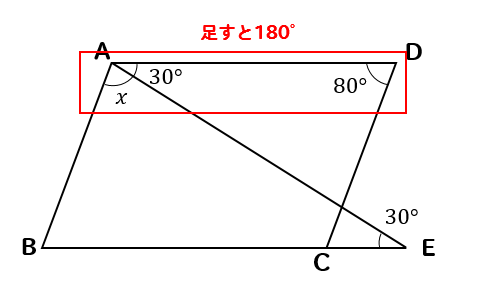
錯角を利用するパターン
四角形ABCDが平行四辺形のとき、\(x\)の値を求めなさい。
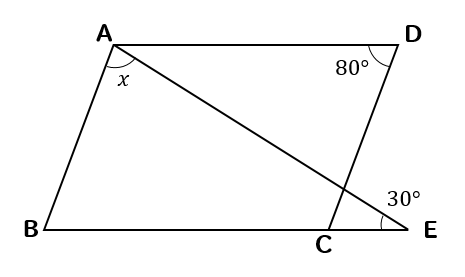
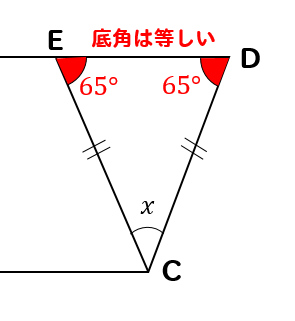
二等辺三角形との融合パターン
四角形ABCDが平行四辺形のとき、\(x\)の値を求めなさい。
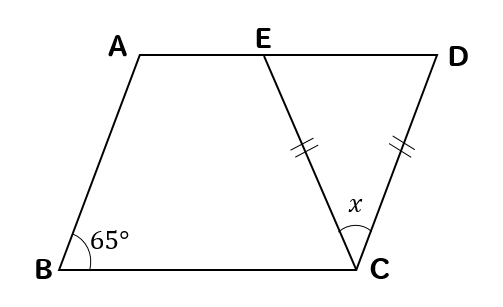
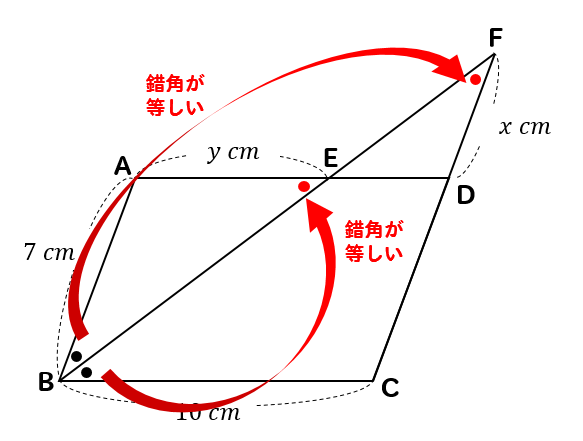
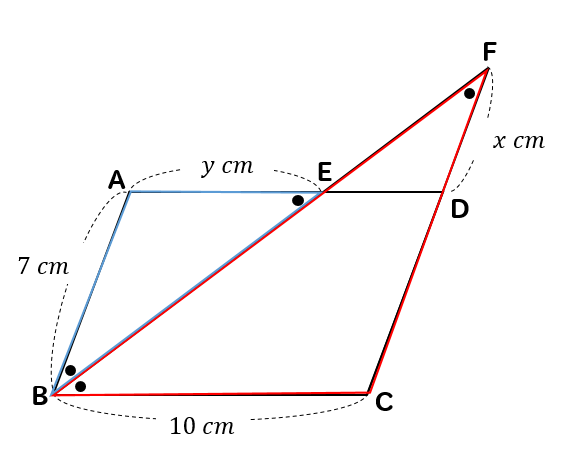
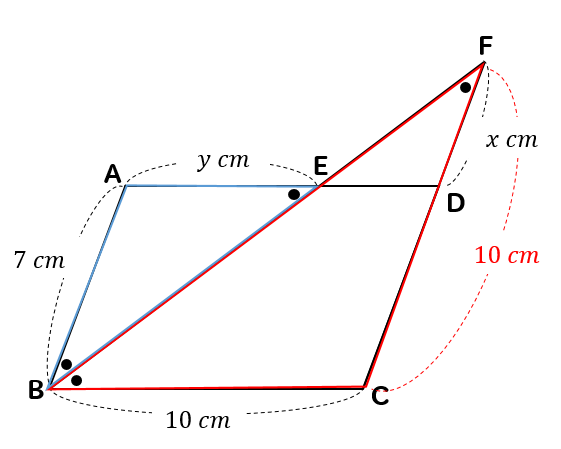
二等辺三角形を見つける発展パターン
四角形ABCDが平行四辺形のとき、\(x,y\)の値を求めなさい。

平行四辺形の角度、辺の長さ まとめ
お疲れ様でした!
平行四辺形の角度、辺の長さ問題では
そこまで『難しい…』と困ってしまうようなものはありませんね。
平行四辺形の基本性質を覚えておくだけで簡単に解けるものばかりです。
平行四辺形の基本性質
- 対辺はそれぞれ平行
- 対辺はそれぞれ等しい
- 対角はそれぞれ等しい
- 対角線はそれぞれの中点で交わる
しっかりと覚えておきましょー!!
【証明の書き方】合同な三角形の証明問題の書き方を基礎から解説!
【直角三角形】証明問題の書き方とは?合同条件の使い方を徹底解説!
平行四辺形の角度、辺の長さを求める問題を解説!←今回の記事



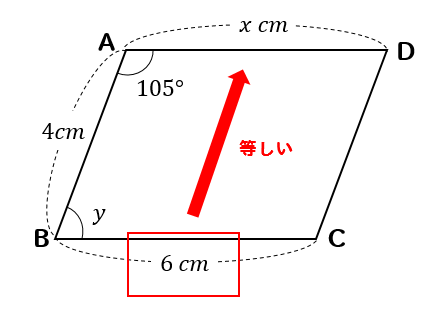
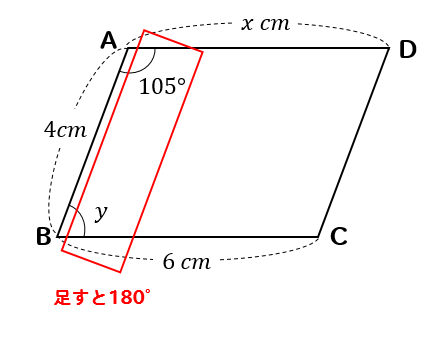

















わかった
わかりやすい