【高校入試】関数の入試問題を解説～第1回～　難関高校の問題に挑戦！

今回は、難関高校の入試問題で出題された関数の問題に挑戦してみよう！

難易度的には「ちょいムズ」です。

公立高校を受験される方にとっては、もしかしたら必要ないレベルかもしれません。

ですが、なるべく丁寧な解説をつけますので

向上心のある方は是非挑戦してもらって、学力アップを目指してもらいたい。

関数の入試問題～第1回～

問題

下の図のように、\(x\)軸上の点A\((-2,0)\)と放物線\(y=x^2\)上の点Bがあり、点Bの\(x\)座標は正である。放物線\(y=x^2\)上にAB//OCとなるように点Cをとると、AB=2OCとなった。

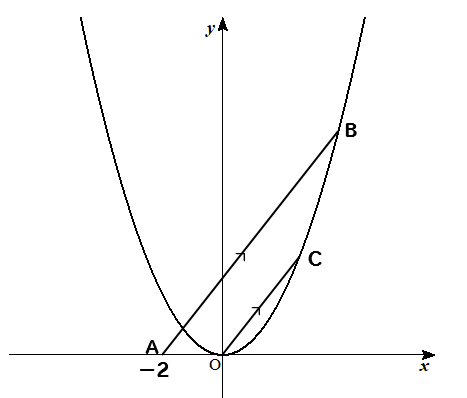
（1）直線BCと\(x\)軸の交点の座標を求めなさい。

（2）点Cの座標を求めなさい。

（3）四角形AOCBの面積を求めなさい。

（1）の解答＆解説

直線BCと\(x\)軸との交点を分かりやすくするために点Dとしておきましょうか。

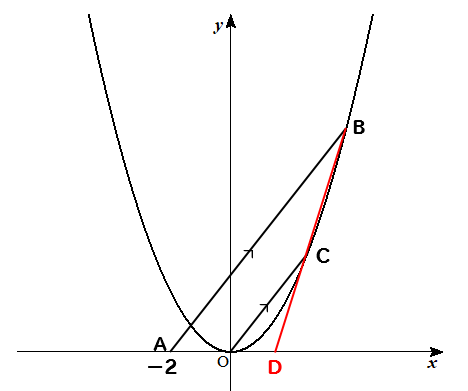
さて、どうやって点Dの座標を求めていけば良いでしょうか。

関数の問題で平行な直線が出てきたときに意識したいのは次の2点。

だいたいの問題ではこれらの知識を使って問題を解かせることになります。

忘れたよって人は、こちらの記事を見直しておいてね。

【等積変形】三角形の面積問題と作図のやり方は？

【相似】平行線と比の利用、辺の長さを求める方法をまとめて問題解説！

今回の問題では、平行な線を利用して

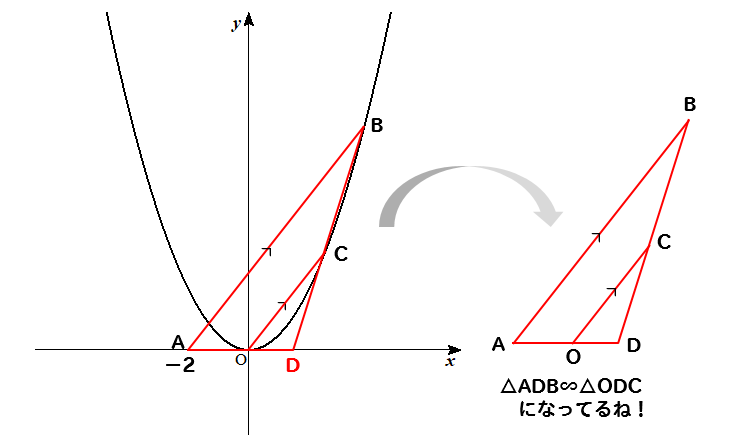
このように相似な三角形を見つけることができるので、平行線と線分の比を利用して問題を解いていきます。

それでは、△ADBと△ODCに注目して線分の比を比較していきます。

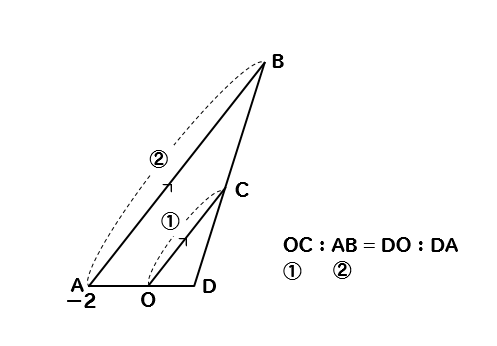
問題文から\(AB=2OC\)とあるので

$$OC:AB=1:2$$

ということが分かります。

よって

$$OC:AB=DO:DA$$

$$1:2=DO:DA$$

となります。

そして、DOの長さを\(x\)とすると

DAの長さはDO+OAだから\(x+2\)となります。

これらを先ほどの比に当てはめて考えると

$$1:2=x:(x+2)$$

$$2x=x+2$$

$$x=2$$

となり、\(DO=2\)だから

点Dの座標は、\((2,0)\)となります。

（2）の解答＆解説

点Cの座標を求めるために、まずは座標を文字で置いてやりましょう。

点Cの\(x\)座標を、\(c\)とすると

点Cは\(y=x^2\)上にあることを利用して、\(y\)座標は\(c^2\)となります。

よって、点Cの座標は\((c,c^2)\)と表せます。

更に、点Cは原点から横に\(c\)、縦に\(c^2\)だけ動いた場所にあるということが読み取れます。

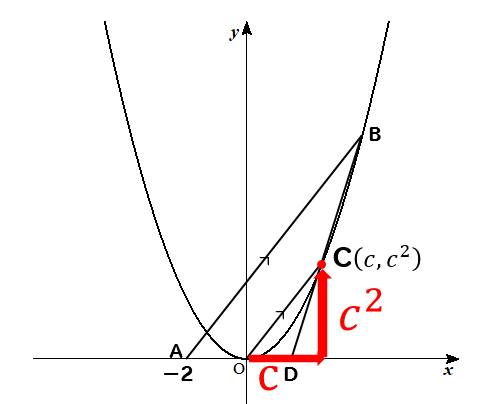
そうするとOCと平行で2倍の長さがあるABの場合

点Bは、点Aから横に\(2c\)、縦に\(2c^2\)だけ動いた場所にあるということになります。

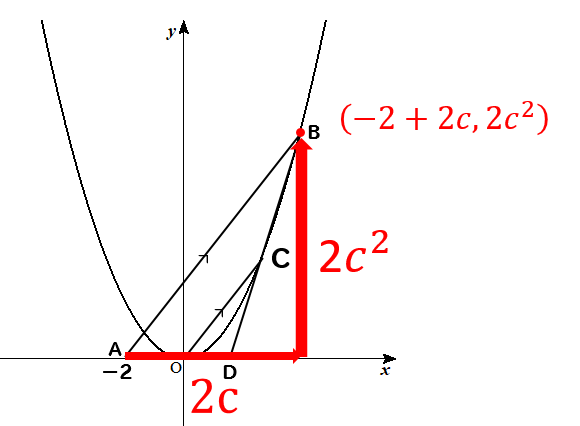
よって、点Bの座標を\((-2+2c,2c^2)\)と表すことができます。

更に、点Bは放物線\(y=x^2\)上にあることから

\(x=-2+2c\)と\(y=2c^2\)を\(y=x^2\)に代入しても等式が成り立ちます。

よって

$$2c^2=(-2+2c)^2$$

$$2c^2=4-8c+4c^2$$

$$2c^2-8c+4=0$$

$$c^2-4c+2=0$$

$$c=\frac{4\pm \sqrt{16-8}}{2}$$

$$c=\frac{4\pm 2\sqrt{2}}{2}$$

$$c=2\pm \sqrt{2}$$

グラフを見る限り、\(c>2\)となるはずだから

$$c=2+\sqrt{2}$$

ということが分かります。

$$c^2=(2+\sqrt{2})^2=6+4\sqrt{2}$$

よって、点Cの座標は\((2+\sqrt{2},6+4\sqrt{2})\)となります。

（3）の解答＆解説

四角形のまま面積を求めようとすると難しくて混乱していまいます。

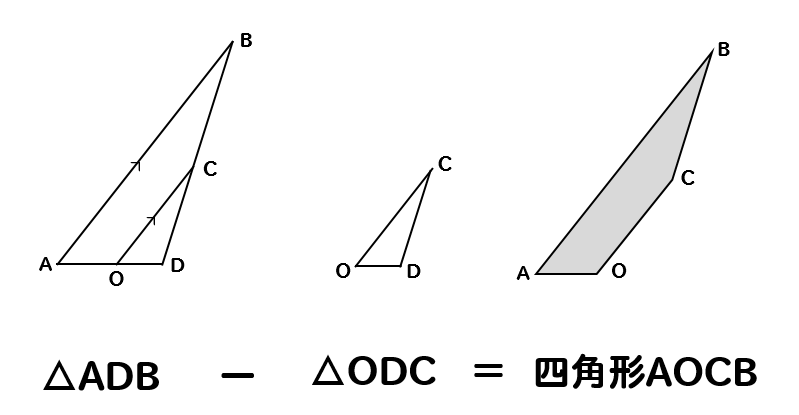
このように大きい三角形から小さい三角形を引くという考えを利用して四角形AOCBの面積を求めていきましょう。

それでは、まず△ODCの面積を求めます。

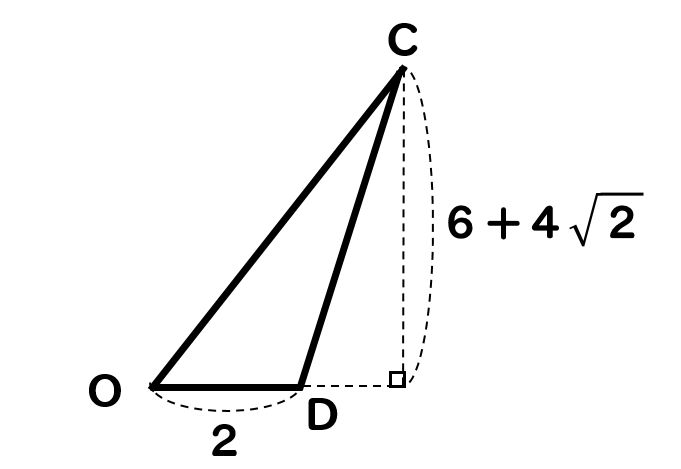
点D、Cの座標からそれぞれの長さを求めて面積を求めると

$$△ODC=2\times (6+4\sqrt{2})\times \frac{1}{2}$$

$$=6+4\sqrt{2}$$

次に△ADBの面積を求めるのですが、これは相似の関係を使うことで楽に求めることができます。

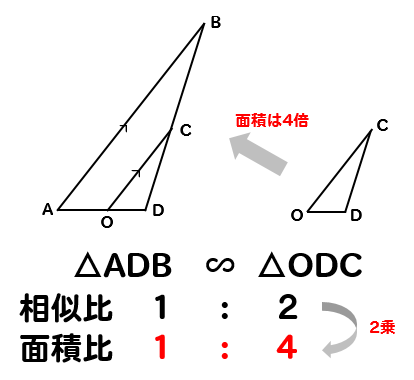
相似比と面積比の関係から考えると

△ADBは、△ODCの面積を4倍したものだと分かります。

よって

$$△ADB=(6+4\sqrt{2})\times 4$$

$$=24+16\sqrt{2}$$

それぞれの面積が求まったので

四角形AOCBの面積は

$$(24+16\sqrt{2})-(6+4\sqrt{2})$$

$$=18+12\sqrt{2}$$

まとめ

お疲れ様でした！

この問題をノーヒントで解けた人は素晴らしいです＾＾

一発で解くことができなかった人も解説を読んで理解してもらえれば、必ず今後のテストで生かされてくるはずです。

演習あるのみ！

ファイトだー(/・ω・)/

【高校入試】関数の難関入試問題を解説～第2回～　グラフから面積の比を考える！