今回は中2で学習する
『合同な図形』の基本性質について解説していくよ!
- 合同な図形ってなに?
- どんな性質があるの?
- どんな問題が出るの?
- 合同な図形の見つけ方って?
この4点についてのお話です(^^)
今回の記事内容は、こちらの動画でも解説しています(/・ω・)/
合同な図形ってなに?
合同な図形っていうのは
ぴったり重なる図形!
という意味です。
つまり、形も大きさも全く同じ図形のこと。
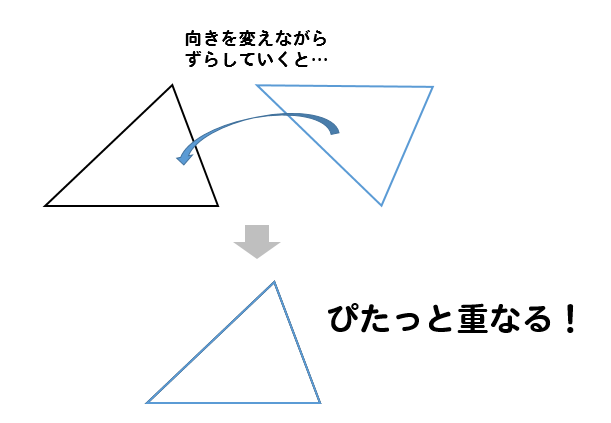
このように2つの図形がぴったり重なる場合に
2つの図形は合同な図形といいます。
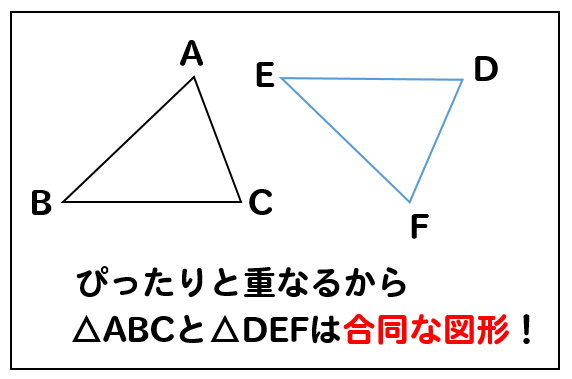
そして
この『重なる』という表現を
数学では『対応する』という言葉を使って表します。
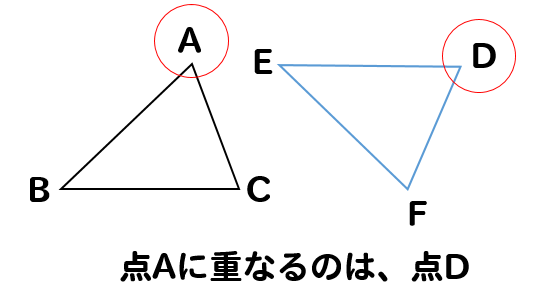
点Aに対応するのは
⇒ 点Aに重なるところだから、点Dとなります。
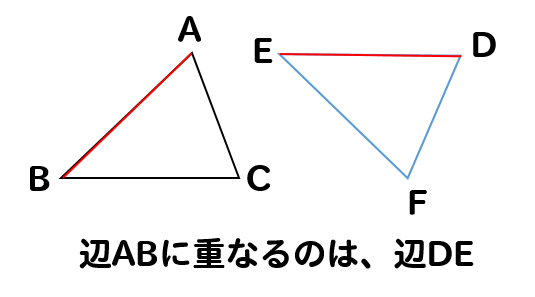
辺ABに対応するのは
⇒ 辺ABに重なるところだから、辺DEとなります。
というように表していきす。
『対応する・・・』という表現を覚えておいてね
問題でたくさん出てくるよ!
そして
2つの図形が合同だよ!ってことを表すときに使う記号がコレ
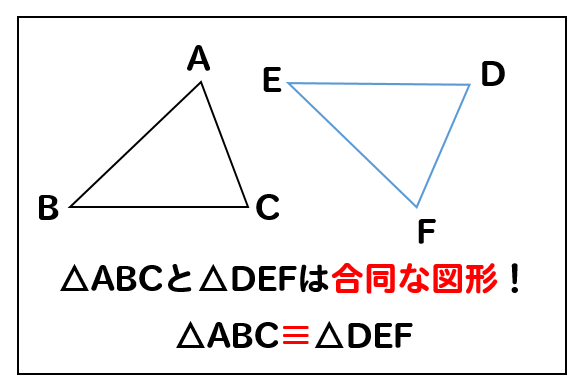
三本線の記号を使って表します。

この記号を使って、合同を表すときに
ちょっとした注意点があるんだよね。
それが
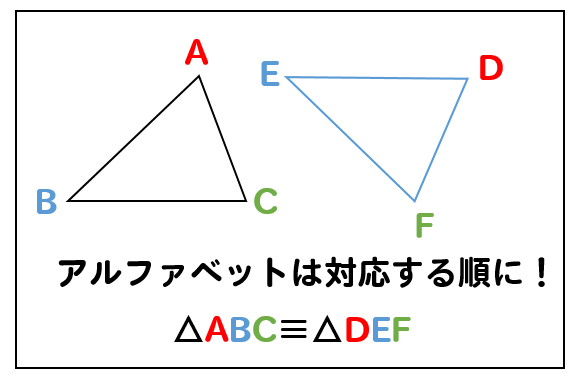
必ず対応する順番に書くこと
図形を表すアルファベットを書くときには
対応する順番、つまり重なる順番に書きましょう。
という決まりがあるから、これも覚えておきましょう!
合同な図形の性質は?
合同な図形とは
ぴったり重なる図形のこと
っていうのは分かってもらえたかな??

それでは、ぴったり重なる合同な図形には
どんな性質があるのかを考えていきましょう。
合同な図形には2つの性質があります。
- 対応する辺の長さが等しい
- 対応する角の大きさが等しい
それぞれ、どんな意味なのか確認していきましょう。
対応する辺の長さが等しいとは?
なんか難しい言葉で言ってるけど
簡単に言い換えると
重なるところは、辺の長さが等しいよね!
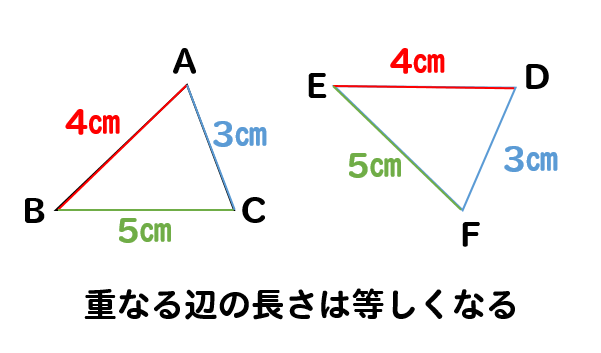
ってこと。
これはイメージ湧くよね?
だって、長さが同じだから
ぴったり重なってるわけだもんね。
対応する角の大きさが等しい
これも言ってることは上と同じようなことです。
重なるところの角は、同じ角度になってるよ!
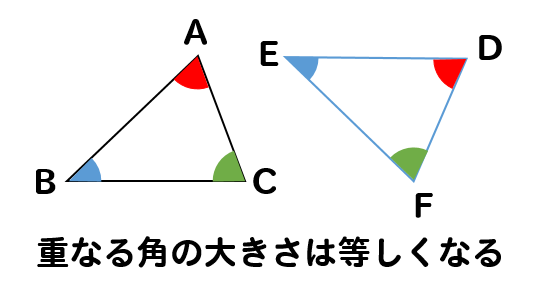
ってこと。
これらの性質を使って
問題を考えていくようになるんだけど
次では、どのように問題が出題されるのか
例題を見ながら一緒に考えていきましょう!
合同な図形の性質を利用した問題とは?
例題
下の図の2つの四角形は合同である。次の問いに答えなさい。
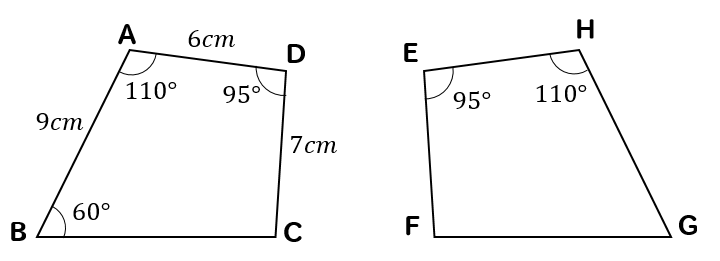
(1)2つの四角形が合同であることを記号を用いて表しなさい。
(2)HEの長さを求めなさい。
(3)∠Gの大きさを求めなさい。
(1)の解説!
(1)2つの四角形が合同であることを記号を用いて表しなさい。
2つの図形は合同なので、『≡』の記号を使って表すことができます。
対応する順に書かなくてはいけないことに注意して
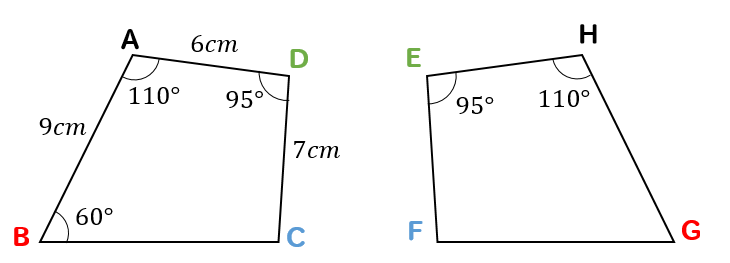
答え
$$\LARGE{{四角形}ABCD \equiv {四角形}HGFE}$$
(2)の解説!
(2)HEの長さを求めなさい。
『合同な図形は、対応する辺の長さが等しい』
という性質を覚えておけば、楽勝な問題です!
辺HEと対応する辺は辺ADなので
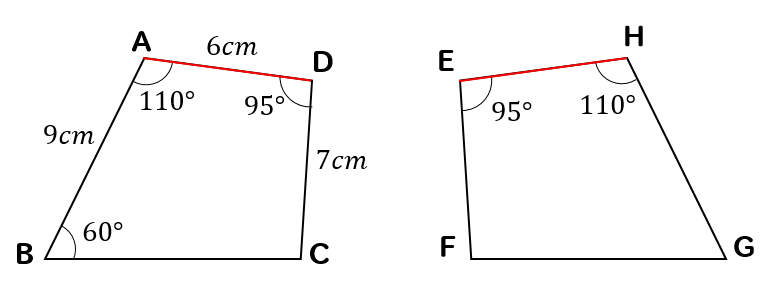
辺HEは辺ADと同じ長さになります。
答え
$$\LARGE{HE=6cm}$$
(3)の解説!
(3)∠Gの大きさを求めなさい。
これも
『合同な図形は、対応する角の大きさが等しい』
ということを覚えておくだけで解けちゃう問題です。
∠Gと対応する角は∠Bです。
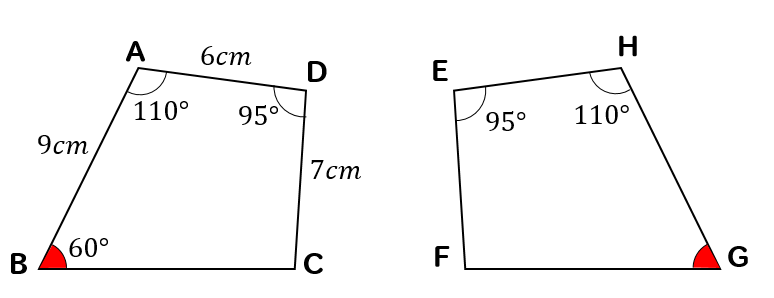
よって、∠Gと∠Bは同じ大きさになるので
答え
$$\LARGE{∠G=60°}$$

合同な三角形の見つけ方とは?
さて、ここまで合同な図形の性質についてお話をしてきました。
合同な図形がどんなもんかってのはわかった!
けどさー
2つの図形が合同になるかどうかって
どうやって判断すればいいの??

2つの図形がぴったり重なるかどうかなんて
テスト中に確かめようがないよね…
そうなんですよね…
ぴったり重ねることができれば合同な図形だ!
とは言いましたが
実際には、ぴったり重なるかどうかを確かめるのが大変なわけですよね…
そこで!
知っておくと、とっても便利な確かめ方法があります。
それが『三角形の合同条件』というものです。
この条件に当てはまる三角形は
わざわざ重ねて確かめなくても
君たちは、合同だ!!

ということが分かっちゃうという便利な条件です。
そんな便利な条件というのが以下の3つです。
- 3組の辺がそれぞれ等しい
- 2組の辺とその間の角がそれぞれ等しい
- 1組の辺とその両端の角がそれぞれ等しい
以上3つのどれかを満たしていれば
その時点で、2つの三角形は合同だということがわかります。
今後、めっちゃくちゃ重要になってくるものだから
絶対に覚えておこう!
合同条件を使った問題や解説は
こちらの記事で詳しくやっていくから
今回の基本性質をマスターできた人は、こちらの記事へ進んでいこう!
>【三角形の合同条件】合同な図形の見つけ方!証明問題の基礎を身につけよう
合同な図形の性質 まとめ
お疲れ様でした!
合同な図形というのは
ぴったり重なる図形のことでしたね。
そして
ぴったり重なる合同な図形には
- 対応する辺の長さが等しい
- 対応する角の大きさが等しい
という性質があります。
これらの性質を利用して
長さや角度を求めたりすることができるようになります。
これは、問題をやってもらったからもうバッチリだね!
そして
合同な三角形を見つけるために重要な
三角形の合同条件というものがありました。
- 3組の辺がそれぞれ等しい
- 2組の辺とその間の角がそれぞれ等しい
- 1組の辺とその両端の角がそれぞれ等しい
これらの条件もしっかりと覚えておこうね!
以上が合同な図形の基本内容でした!
ここから発展して
証明問題などに繋がっていくわけですが
今後の内容につまづいたときには、この基本に立ち返ることが大切です。
それでは、次の単元もがんばって学習していきましょー!
ファイトだー(/・ω・)/
合同な図形の基本性質とは?←今回の記事
【証明の書き方】合同な三角形の証明問題の書き方を基礎から解説!
【直角三角形】証明問題の書き方とは?合同条件の使い方を徹底解説!

















コメントを残す