この記事では、高校入試に出題された作図問題の解き方を解説していきます。
数学の入試問題では
作図は必ずと言ってもいいくらい出題される
必須の問題ですね！
しっかりと対策しておけば
得点源にすることができる単元でもあるので
この記事を通して、作図問題をマスターしていきましょう！
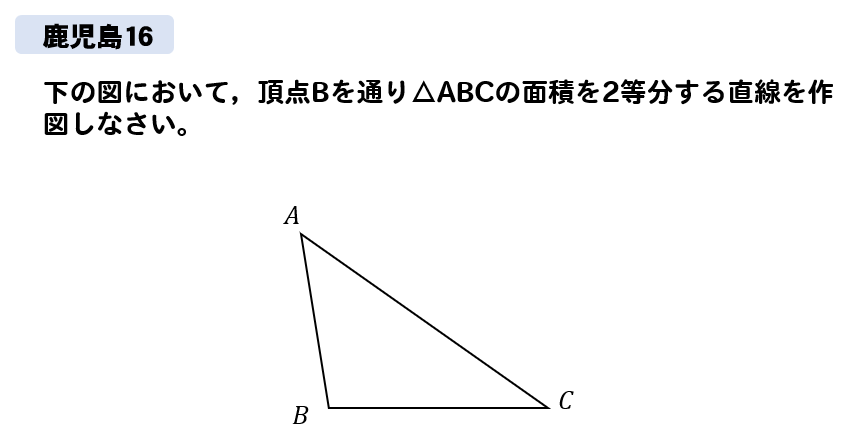
では、入試問題から抜粋した問題に挑戦してみましょう。
作図の入試問題に挑戦！
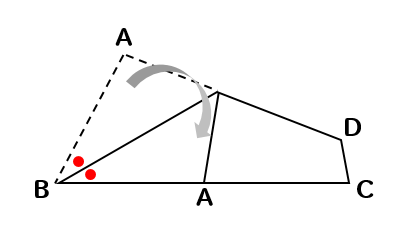
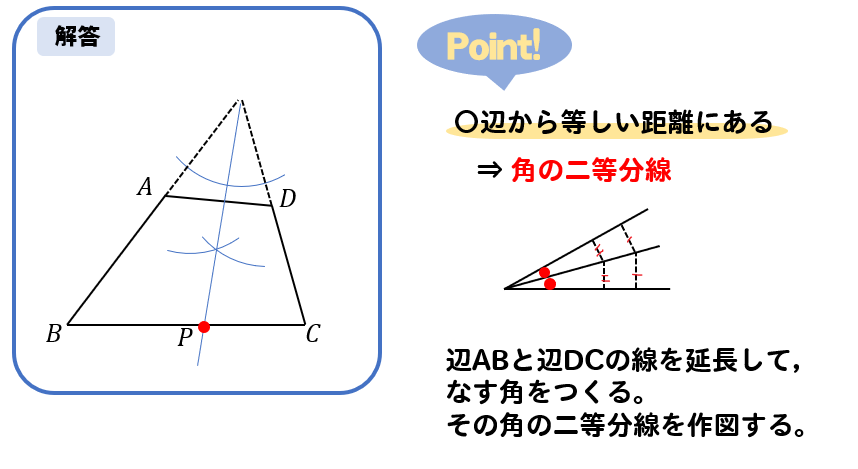
下の図の四角形ABCDにおいて、辺ABと辺BCが重なるように折ったときにできる折り目の線と辺ADとの交点をPとします。点Pを定規とコンパスを使って作図しなさい。
この問題のポイントは
辺ABを辺BCに重ねるように折ったときに
どのような折り目ができるかを考えることです。
上の図からわかるように
折り目は∠Bを二等分した線になっています。
よって、∠Bの二等分線を書いて
その線が辺ADとぶつかったところが点Pとなります。
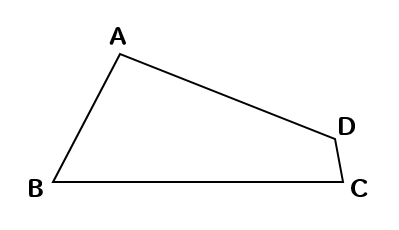
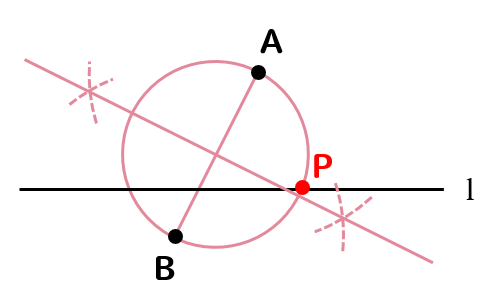
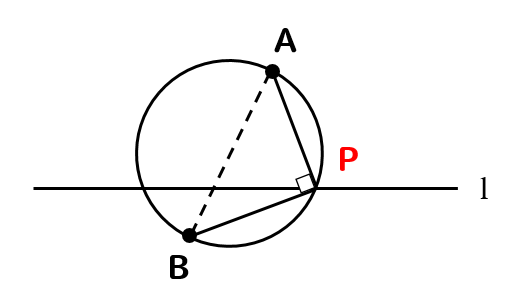
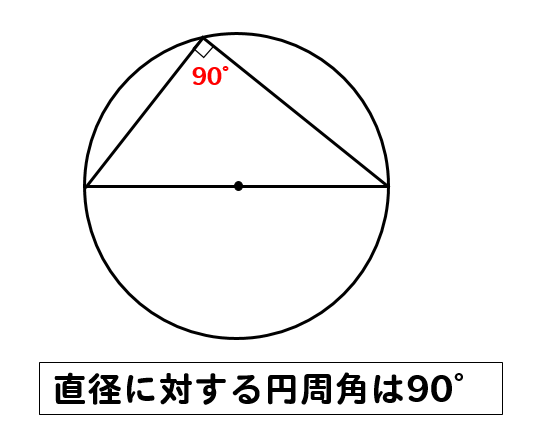
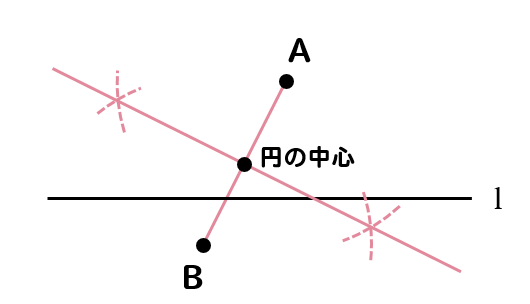
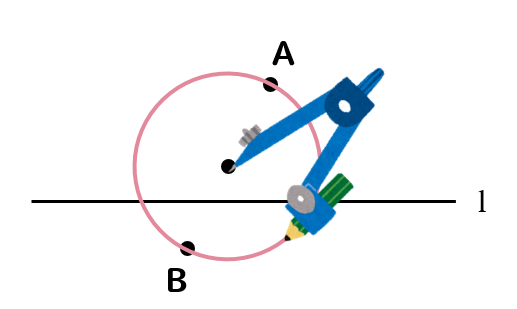
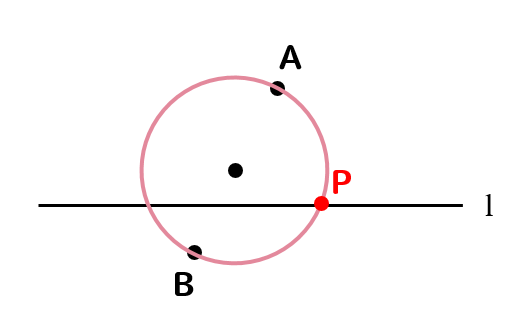
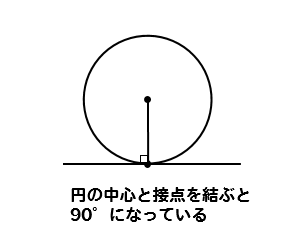
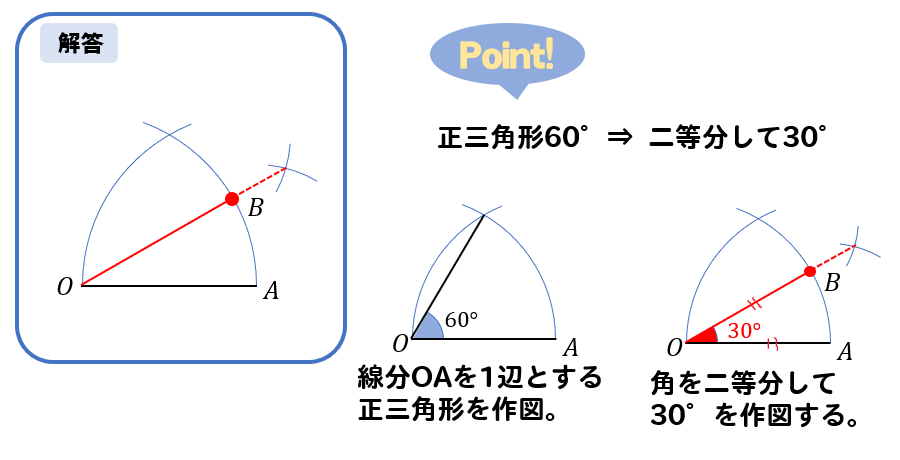
下の図のように、直線lと直線l上にない2点A、Bがあります。直線l上に点Pをとるとき、∠APB＝90°となる点Pのうちの1つを、コンパスと定規を使って作図しなさい。
答え
今回の問題のポイントは
辺ABを直径とする円を考えると
このように90°の角を作図できるということに気づけたかどうかですね。
なんでコレで90°が作れるの？？
という方は円周角の定理を復習しておいてね。
それでは、辺ABを直径とする円を作図するために
まずは円の中心を求めます。
ABの垂直二等分線を作図すれば、円の中心を求めることができます。
中心が求まれば、中心にコンパスの針を置いて
A、Bを通るように円を作図してやりましょう。
そうすれば、円と直線lがぶつかったところが点Pとなります。
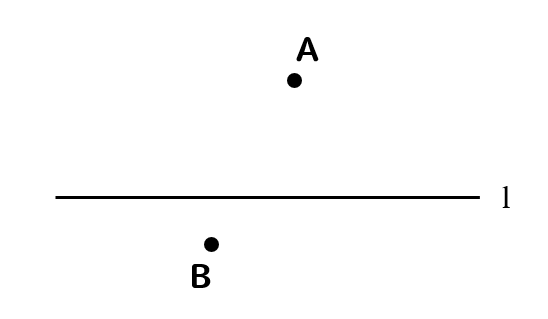
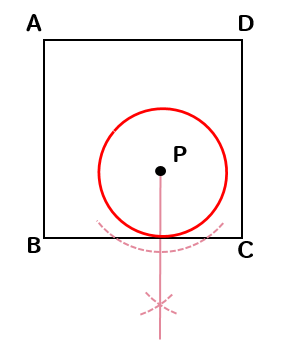
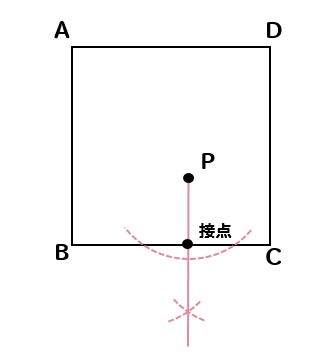
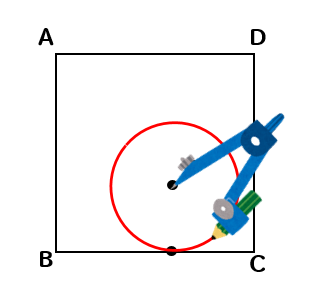
正方形の紙の上に点Pがある。この紙から、点Pを中心とする半径が最も大きい円を切り取る。下の図は、正方形の紙と同じ大きさの正方形ABCDをかき、点Pの位置を示したものである。切り取る円を、定規とコンパスを用いて作図しなさい。
答え
半径が最も大きくなるのは
辺BCを接線に持つように円を作図したときになります。
中心と接点を結んだ線は、接線と垂直な関係にあることを考えると
点Pから辺BCに垂線を引いてやることで
接点を求めてやることができます。
接点が求まると
点Pにコンパスの針を置いて、接点を通るように円を作図すれば完成です！
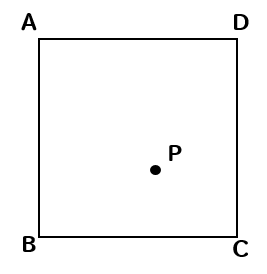
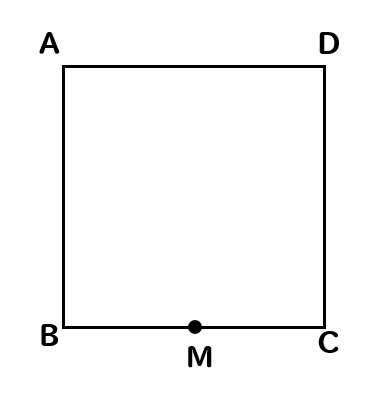
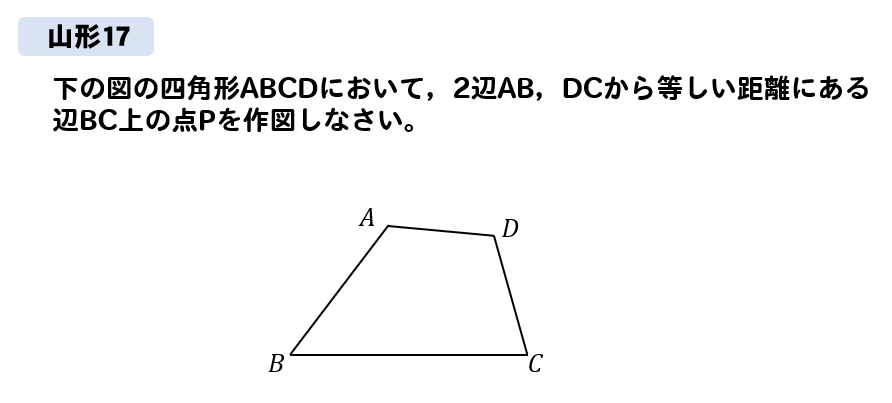
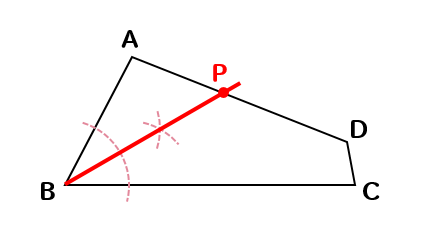
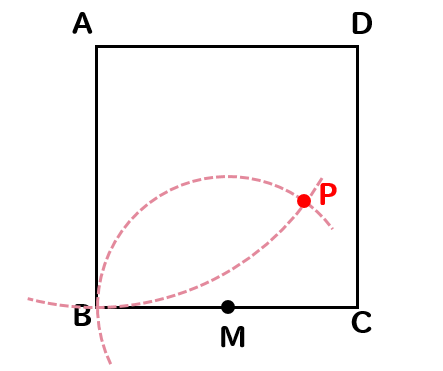
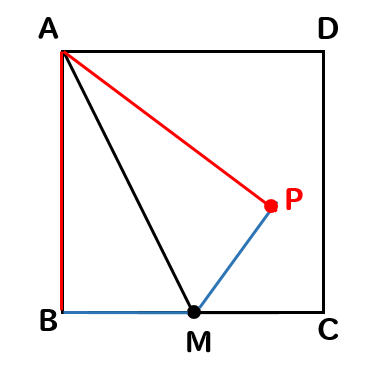
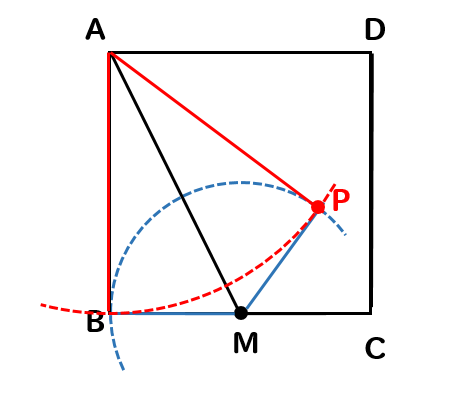
下の図のような正方形ABCDがある。辺BCの中点をMとする。
このとき、線分AMを折り目として折り返したときの点Bの位置を点Pとする。このとき、点Pを作図しなさい。
答え
折り返したときのイメージを考えてみましょう。
すると
AB=AP
BM=PMとなることがわかりますね。
このことから点Pは
点Aを中心とする半径ABとなる円
点Mを中心とするBMを半径とする円を
それぞれ作図することによって見つけることができます。
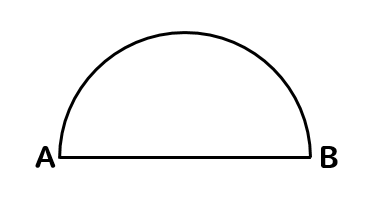
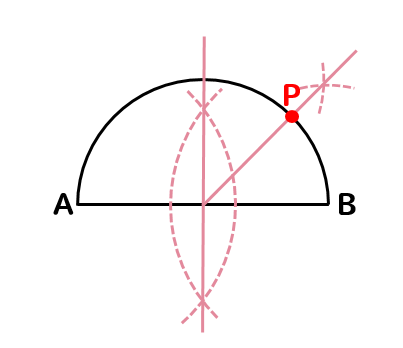
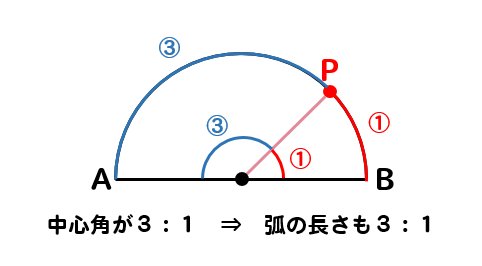
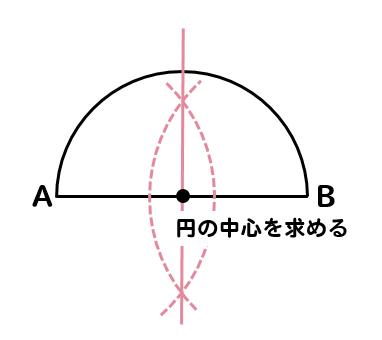
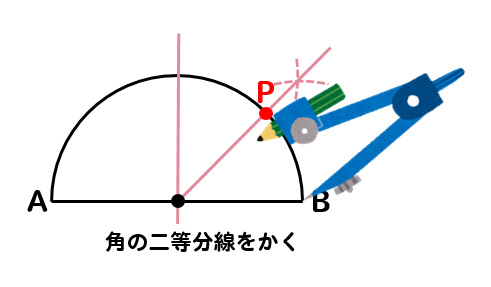
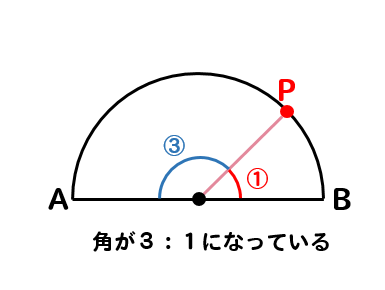
下の図のような、線分ABを直径とする半円がある。この半円の弧AB上に弧APと弧PBの長さの比が3:1となる点Pをコンパスと定規を使って作図しなさい。
答え
解法のポイント弧の長さを3:1にするということは
中心角の大きさを3:1にすればよいということ。
中心角が3:1になるような線を引くために
ABの垂直二等分線を作図することで
半円の中心を求めます。
中心を求めることができれば
角の二等分線の作図を利用して
このように角を3:1にわけてやれば完成です。
入試の作図問題 まとめ
お疲れ様でした！
全部解けましたか？？
定期テストには出題されないような
ちょっと応用な問題ばかりですが
使っている作図方法は
- 垂直二等分線
- 垂線
- 角の二等分線
この３つの組み合わせによるものばかりです。
しっかりと過去問演習を重ねていけば
本番では必ず解けるようになるはずです。
とにかく演習あるのみ！
ファイトだー(/・ω・)/
作図をもっと演習したいあなた！
作図に対して、このような悩みはありませんか？
- 作図が出ると諦めてしまう
- どうやって勉強すればいいか分からない
- 作図の問題が手に入らないから演習できない
- 基本はできるけど、模試になるとダメ
- 問題集の解説が分かりにくくて理解できない
正しい作図の学び方を実践すれば、あなたも今すぐこのような変化が手に入りますよ！
- 作図がスラスラ解けるようになり、数学の点数がアップする
- テストで作図が出てくると、簡単に解くことができるので嬉しい気持ちになる
- 模試に出てくる難しい作図もバッチリ！得点が安定するようになる
- 作図に対する悩みが解消されて、入試に対する不安がなくなる
- たくさんの演習を通して、作図に自信が持てる
- 図形の理解が深まり、図形の大問が解けるようになる
- 友達に作図を教えてあげて、頼られる存在になる
- 高校生になったとき、同級生たちよりも数学が得意になれる
今すぐこちらをクリックして、正しい学び方を手に入れてください！
数学の成績が落ちてきた…と焦っていませんか？
数スタのメルマガ講座（中学生）では、以下の内容を無料でお届けします！
① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ テストで得点アップさせるための限定動画
④ オリジナル教材の配布など、様々な企画を実施！
今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
この前のVもぎでた類似問題が3つある！
普通にすごい。
それは良かった！
入試本番でも類似問題が出るといいなー
本当に助かっています！ありがとうございます。
ありがとうございます！
受験勉強がんばってくださいね(^^)
解説も分かりやすい！
がんばって作ったので嬉しいです！
他の記事もご活用くださいね！
とても、分かりやすく受験生なんですけど、とても役に立ちました。ありがとうございます。これは、数学だけですか？社会や理科はあるのですか？
お役に立ててうれしいです＾＾
社会のサイトはこちらにありますよ！
⇒ https://social-line.com/