二次関数 kaztastudy

高校数学で学習する連立方程式の解き方まとめ！




高校数学で学習する「連立方程式の解き方」についてまとめていきます。

 

高校数学で学習するような連立方程式とは、

次のようなものになります。

【問題】

次の連立方程式を解け。

\begin{eqnarray}（1）\left\{\begin{array}{l}x + y = -2 \\x y = -3\end{array}\right.\end{eqnarray}

\begin{eqnarray}（2）\left\{\begin{array}{l}x + y = 5 \\x^2+y^2 = 17\end{array}\right.\end{eqnarray}

\begin{eqnarray}（3）\left\{\begin{array}{l}x^2+y^2=1 \\x^2+y^2-x+y=2\end{array}\right.\end{eqnarray}

\begin{eqnarray}（4）\left\{\begin{array}{l}x^2-3xy+2y^2=0 \\x^2+y^2+x-y=4\end{array}\right.\end{eqnarray}

\begin{eqnarray}（5）\left\{\begin{array}{l}x-y+z=1 \\4x-2y+z=-6 \\9x+3y+z=9\end{array}\right.\end{eqnarray}

 

これらの連立方程式を解くためには、中学で学習する「加減法」「代入法」のやり方を理解している必要があります。

【参考】

>【連立方程式】加減法の解き方をわかりやすく問題を使って徹底解説！

>【連立方程式】代入法の解き方をわかりやすく問題を使って徹底解説！

不安がある方は、こちらで復習しておいてくださいね(^^)

高校で学習する連立方程式の解き方

（1）の解き方、考え方

【問題】

次の連立方程式を解け。

（1）\begin{eqnarray}\left\{\begin{array}{l}x + y = -2 \\x y = -3\end{array}\right.\end{eqnarray}

文字を消去すべし！

\(x+y=-2\) ⇒ \(y=-2-x\) と変形して、代入法を用いて解いていきましょう。

（2）の解き方、考え方

【問題】

次の連立方程式を解け。

（2）\begin{eqnarray}\left\{\begin{array}{l}x + y = 5 \\x^2+y^2 = 17\end{array}\right.\end{eqnarray}

こちらも(1)と同じように、文字を消去することを考えましょう。

一次式である \(x+y=5\) を変形して、\(x^2+y^2=17\) に代入して解いていきます。

 

（3）の解き方、考え方

【問題】

次の連立方程式を解け。

（3）\begin{eqnarray}\left\{\begin{array}{l}x^2+y^2=1 \\x^2+y^2-x+y=2\end{array}\right.\end{eqnarray}

（1）（2）とは違い、文字を消去するために工夫が必要になります。

まずは、2つの式を利用して \(y=\cdots \) の形が作れないか考えてみてください。

 

 

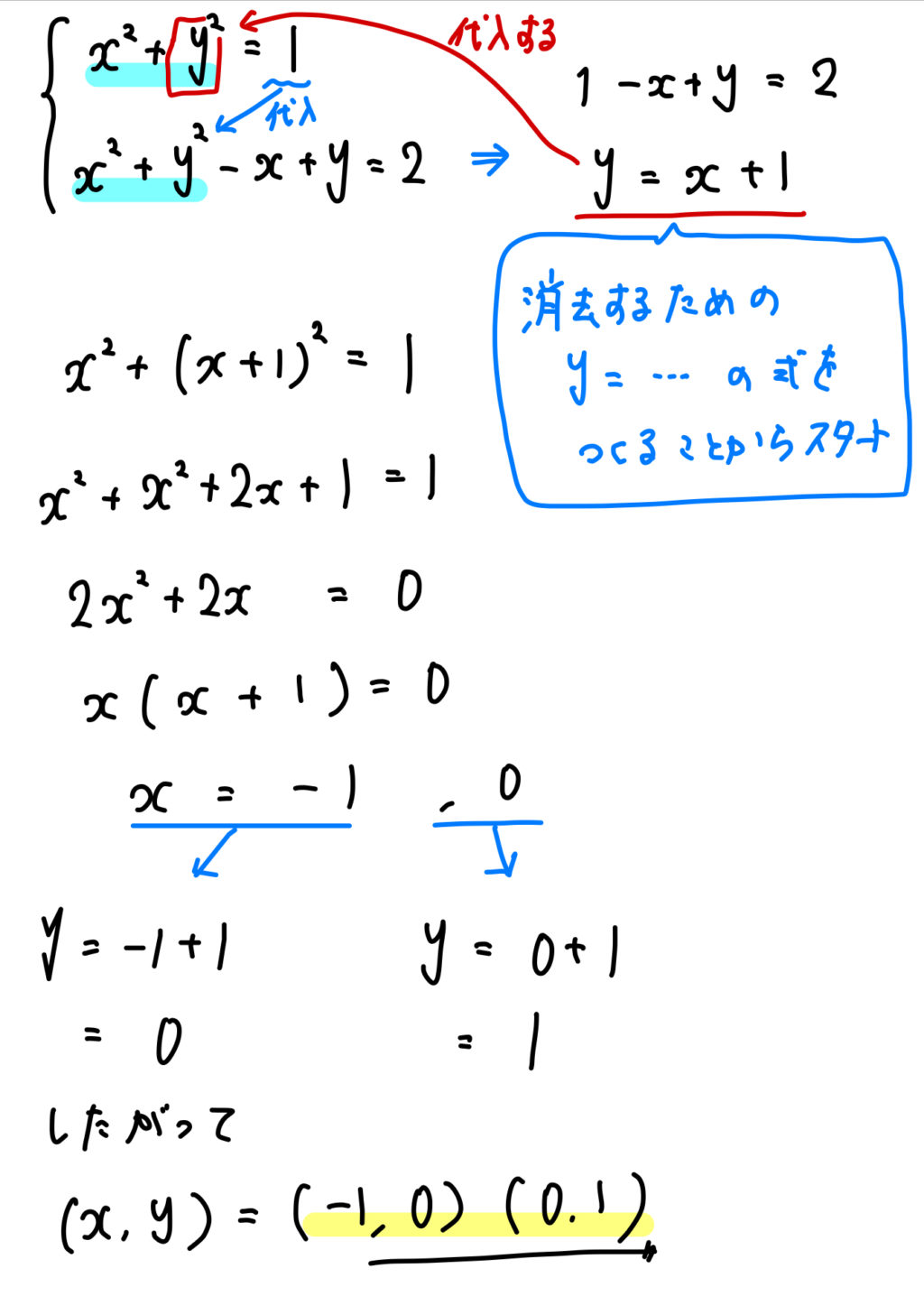
（4）の解き方、考え方

【問題】

次の連立方程式を解け。

（4）\begin{eqnarray}\left\{\begin{array}{l}x^2-3xy+2y^2=0 \\x^2+y^2+x-y=4\end{array}\right.\end{eqnarray}

こちらの連立方程式は文字を消去することに苦戦しますね(^^;)

こういう場合には、どちらか因数分解できる方程式を見つけ、そこから\(x\) と\(y\) の関係式を導くようにしてください。

 

（5）の解き方、考え方

【問題】

次の連立方程式を解け。

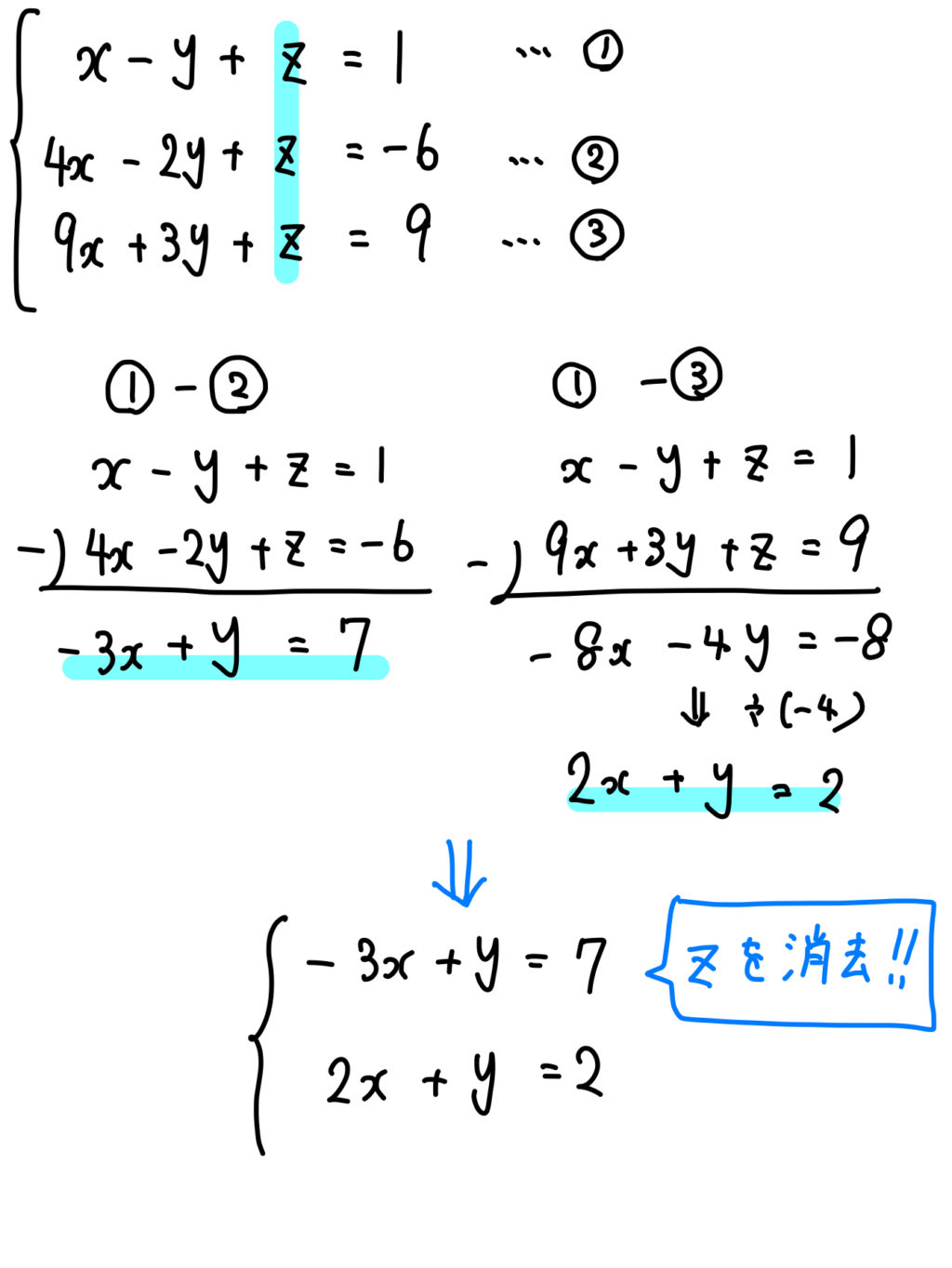
（5）\begin{eqnarray}\left\{\begin{array}{l}x-y+z=1 \\4x-2y+z=-6 \\9x+3y+z=9\end{array}\right.\end{eqnarray}

このように3つ文字を含むような連立方程式のことを、連立3元1次方程式といいます。

この場合には、文字を1つずつ消去して解いていきましょう。

まずは、最初に消去する文字を決めます。

 

係数が揃ってる、揃えやすそうな文字から消去していきましょう。

 

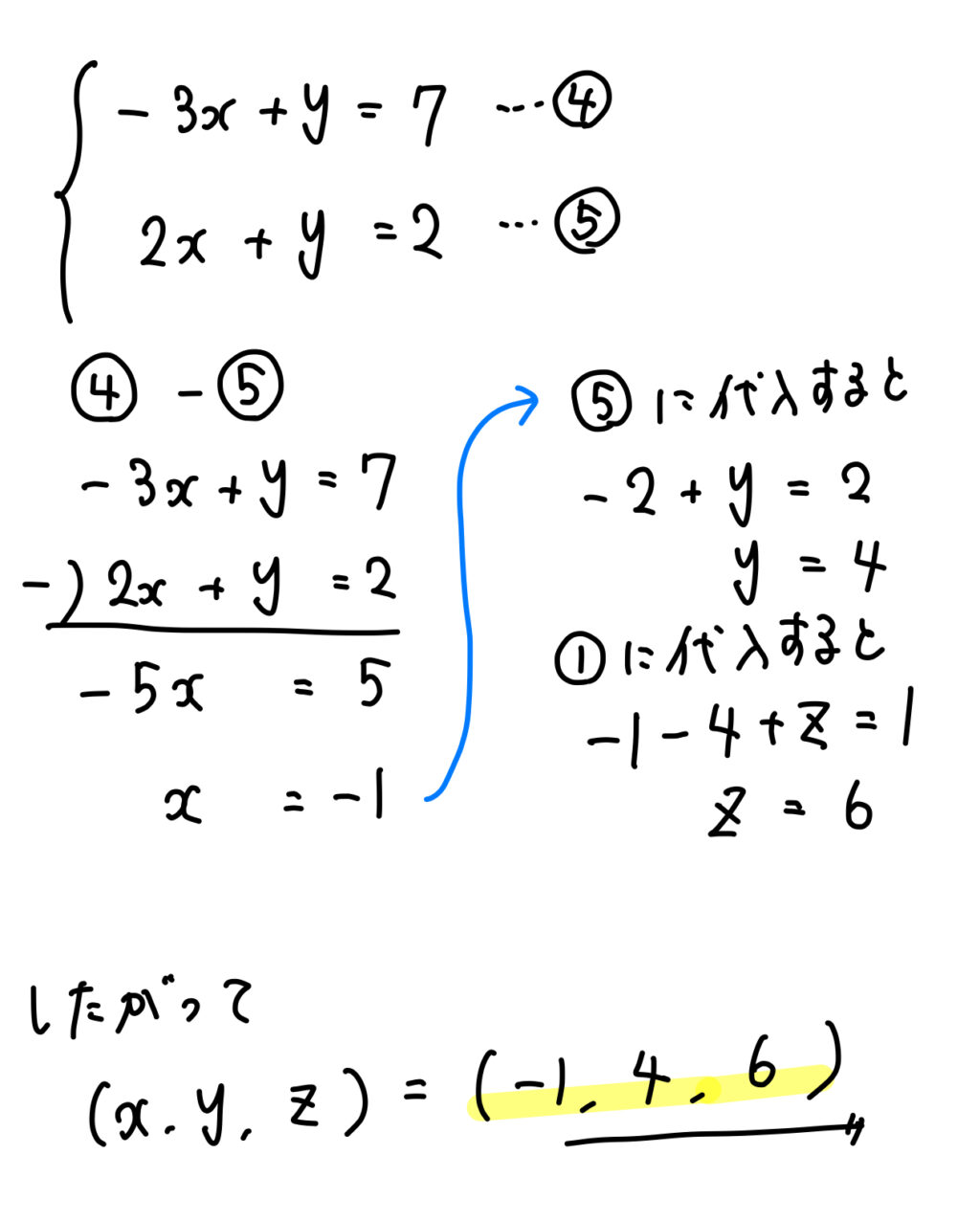
文字を1つ消去することができれば、見慣れた連立方程式の形を導くことができますね！

あとは計算を進めていけばOKです。

まとめ！

お疲れ様でした！

高校で学習する連立方程式はどれも工夫が必要なものばかり。

ですが、すべてに共通していることは

文字を消去すべし！

ということですね。

今回紹介した例題を通して、文字の消去方法について理解しておいてくださいね！

 

こちらの記事も合わせてどうぞ！

 

成績を上げて、志望校合格を勝ち取りたい中3生の方！

数スタの無料メルマガ講座で合格を勝ち取りませんか？

中3受験生向け、メルマガ講座の内容

① 基礎力アップ！点をあげるための演習問題

② 文章題、図形、関数のニガテをなくすための特別講義

③ わからないを解決！質問対応サポート

④ オリジナル教材の配布など、様々な企画を実施！


今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！

数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！

講座を無料で受講する！

 

 

数スタの他記事はこちらから

こちらの関連記事はいかがでしょうか？

コメントを残す

メールアドレスが公開されることはありません。

RECOMMENDこちらの記事も人気です。