今回は二次関数の最大最小を求める問題から「場合分け」が必要なものを取り上げていきます。
この問題を苦手にしている人は多いみたいだね。
だけど、ちゃんと手順をおさえておけば大丈夫!
手順通りにやれば、サクッと解くことができちゃうよ(^^)
ってことで、最大最小の場合分けやっていきましょー!
今回の記事はこちらの動画でも解説しています(/・ω・)/
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
二次関数の最大最小を場合分け!
【問題】
関数\(y=x^2-2ax+1 (0≦x≦2)\) の最大値と最小値、およびそのときの\(x\)の値を求めなさい。
こちらの記事で解説している通り
>【苦手な人向け】二次関数の最大・最小の求め方をイチから解説していきます!
二次関数の最大最小を求めるためには、まずグラフを書きましょう。
$$\begin{eqnarray}y&=&x^2-2ax+1\\[5pt]&=&(x-a)^2-a^2+1 \end{eqnarray}$$
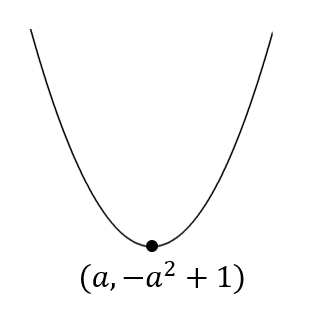
よし、グラフが書けたから定義域の部分で切りとろう!

ってなるねw
頂点の座標に文字が含まれていることによって、定義域の0と2がどの辺りになるのか分かりません…
このように、軸や定義域に文字が含まれていると、どこを切り取っていいか分からなくなってしまいます。
こういったときには、場合分けを使って考えられるすべてのパターンを求めていく必要があるのです。
では、どのようなパターンが考えられるかというと
最小値の場合には次のようになります。
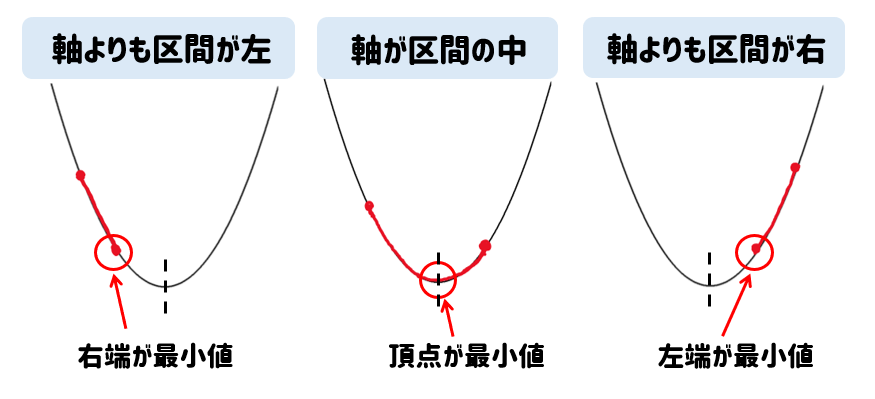
最大値の場合には次のようになります。
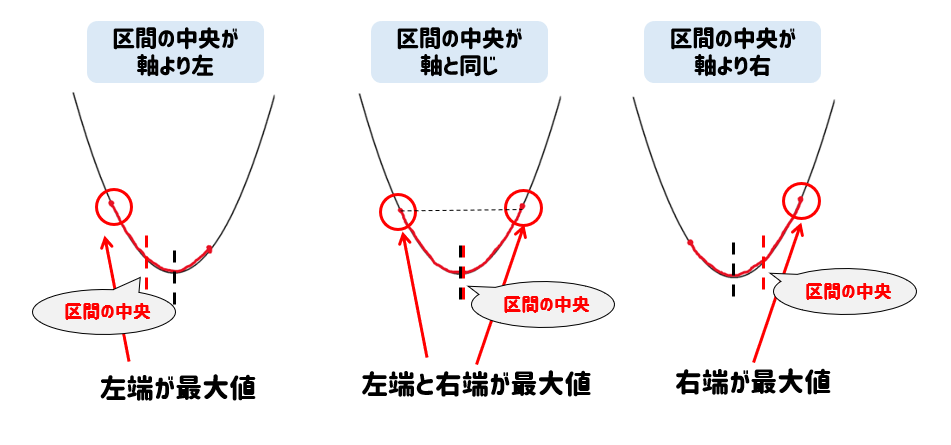
では、これらの場合分けにそって問題を解いてみましょう。
最小値の場合分け
まずは、軸を記したグラフを3つ書きます。
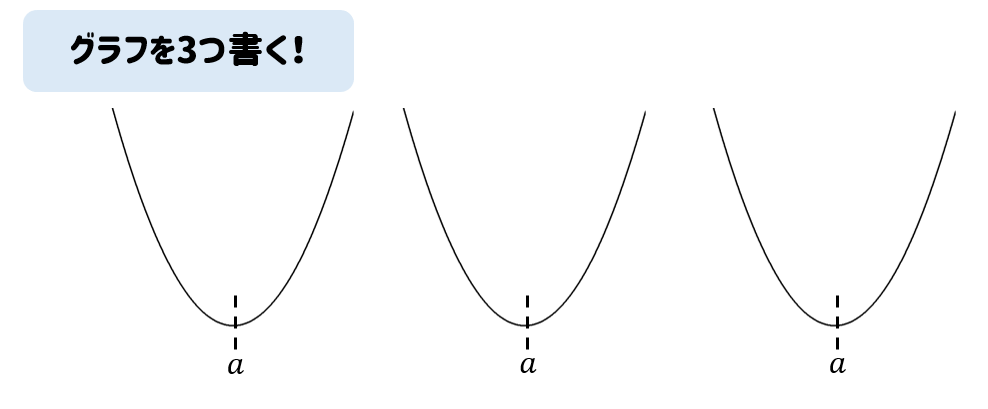
グラフが3つ書けたら、それぞれのグラフ上に区間が左・中・右となるように書いていきます。
このとき区間の0と2という数も記しておきましょう。
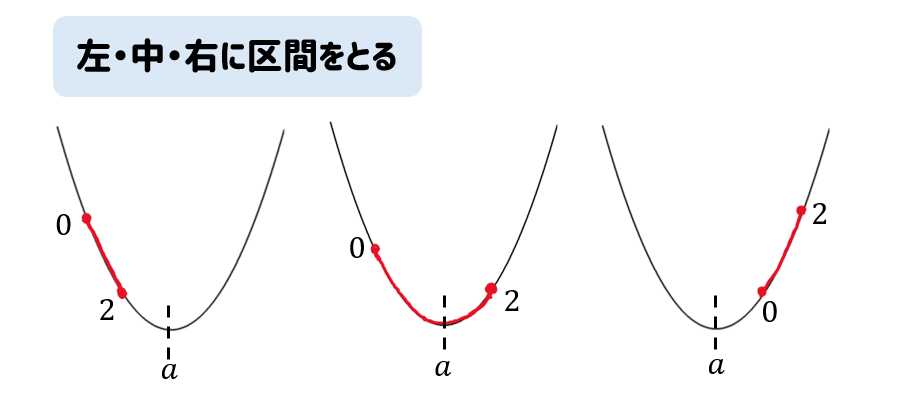
区間がとれたら、どのような条件でそれぞれのパターンになるのかを考えていきます。
まずは区間が軸の左にある場合を考えてみましょう。
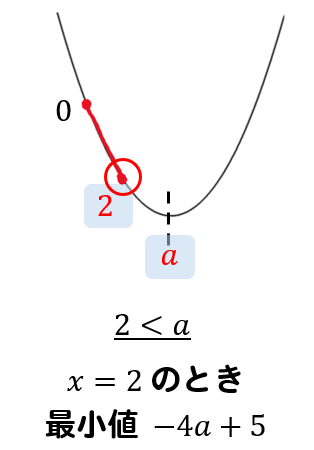
区間の右端が軸よりも左側にある場合ですから
$$2<a$$
という条件になることがわかります。
そして、\(x=2\) のときに最小値になるので二次関数の式に\(x=2\) を代入すると
$$y=2^2-2a\times 2+1=-4a+5$$
となりました。
次に軸が区間の中にある場合
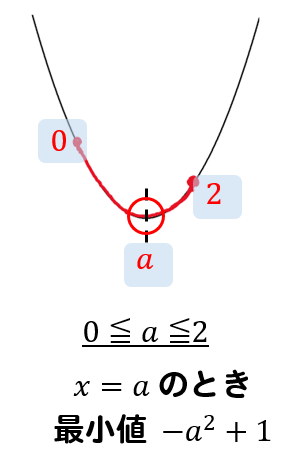
区間0と2の間に軸である\(a\) が入っている場合ですから
$$0≦a≦2$$
という条件になることがわかります。
そして、\(x=a\) のときに最小値になるので頂点の座標を見ると最小値は \(-a^2+1\) となります。
最後に、区間が軸の右にある場合を考えてみましょう。
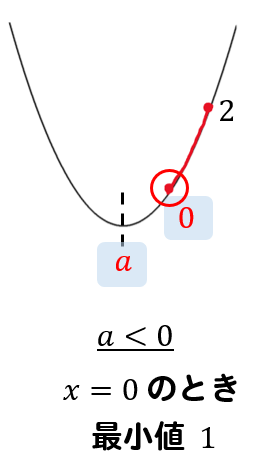
区間の左端が軸よりも右側にある場合ですから
$$a<0$$
という条件になることがわかります。
そして、\(x=0\) のときに最小値になるので二次関数の式に\(x=0\) を代入すると
$$y=0^2-2a\times 0+1=1$$
となりました。
以上、3つの場合分けによって最小値は次のようになります。
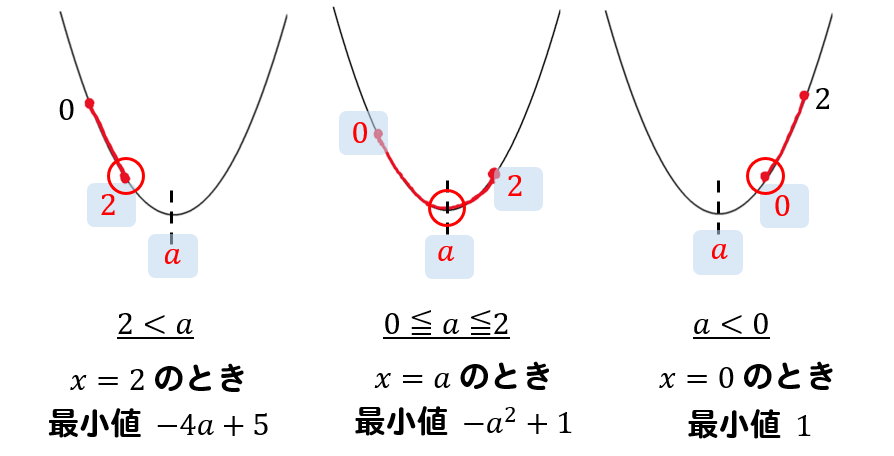
答え
\(2<a\) のとき \(x=2\) で最小値 \(-4a+5\)
\(0≦a≦2\) のとき \(x=a\) で最小値 \(-a^2+1\)
\(a<0\) のとき \(x=0\) で最小値 \(1\)
最小値では、左・中・右と3つのパターンに場合分けするのがポイントですね!
最大値の場合分け
最大値も同じく
まずは、軸を記したグラフを3つ書きます。

次に、区間の左が上になっている、区間の左右が同じ高さになっている、区間の右が上になっている。
この3パターンを図示していきます。
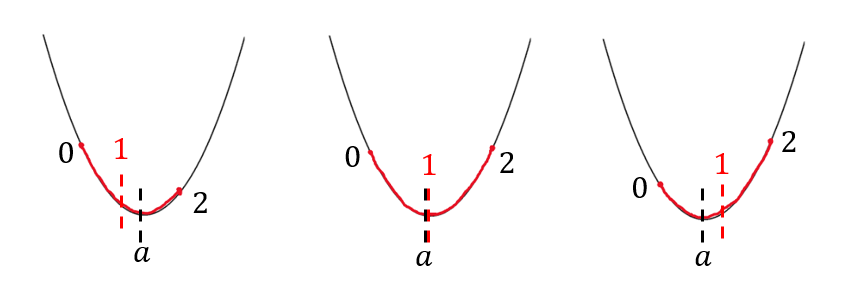
このとき、区間の0と2だけでなく
区間の中央の値である1も図示しておくと後の場合分けがラクになります。
区間の中央の値とは、区間両端の数を足して2で割ると求めることができます。
今回であれば、\(\frac{0+2}{2}=1\) ですね。
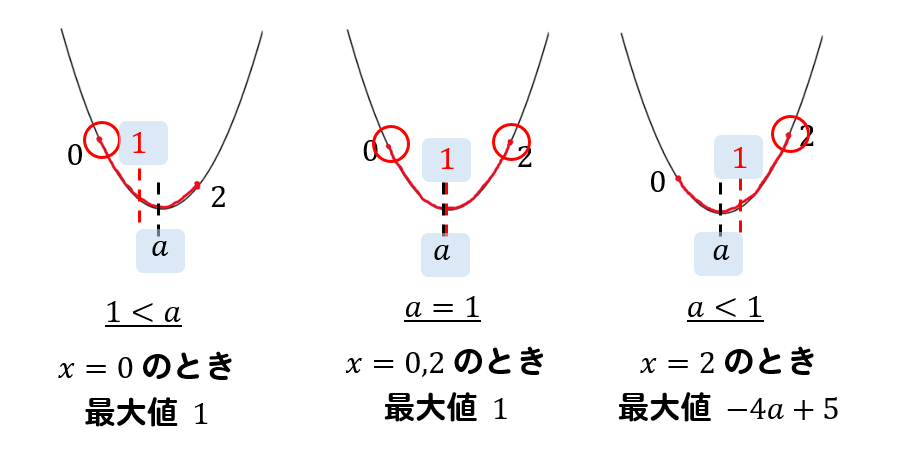
では、まずは区間の左が上がっているパターンから考えてみましょう。

区間の左が最大になるパターンとは、区間の中央が軸よりも左にある場合ですから
$$1<a$$
という条件になることがわかります。
そして、\(x=0\) のときに最大値になるので二次関数の式に\(x=0\) を代入すると
$$y=0^2-2a\times 0+1=1$$
となりました。
次に区間の左右が同じ高さになるパターン
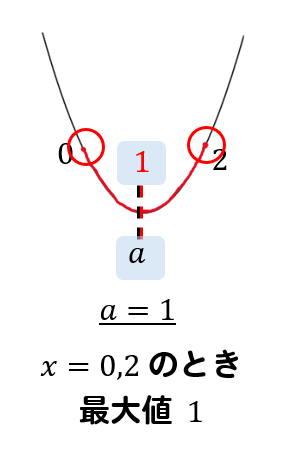
区間の左右が最大になるパターンとは、区間の中央が軸と同じ位置にある場合ですから
$$a=1$$
という条件になることがわかります。
そして、\(x=0,2\) のときに最大値になるので二次関数の式に\(x=0\) を代入すると(\(x=2\)を代入してもOK)
$$y=0^2-2a\times 0+1=1$$
となりました。
最後に、区間の右が上がっているパターン
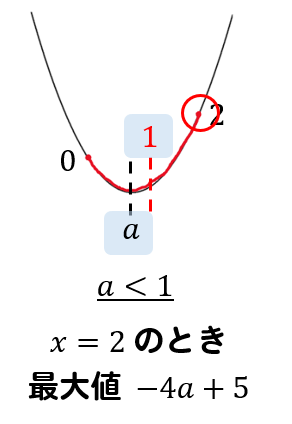
区間の右が最大になるパターンとは、区間の中央が軸よりも右にある場合ですから
$$a<1$$
という条件になることがわかります。
そして、\(x=2\) のときに最大値になるので二次関数の式に\(x=2\) を代入すると
$$y=2^2-2a\times 2+1=-4a+5$$
となりました。
以上、3つの場合分けによって最大値は次のようになります。
答え
\(1<a\) のとき \(x=0\) で最大値 \(1\)
\(a=1\) のとき \(x=0,2\) で最大値 \(1\)
\(a<1\) のとき \(x=2\) で最大値 \(-4a+5\)
最大値では、左・左右・右と3つのパターンに場合分けするのがポイントですね!
場合分けの条件をつくる際には、区間の中央を考える必要があるので覚えておきましょう。
区間に文字が含まれているときの場合分け【練習問題】
では、次に区間に文字が含まれているときの場合分けに挑戦してみましょう。
場合分けの考え方は上でやってきたのと同じです。
では、レッツトライ(/・ω・)/
【問題】
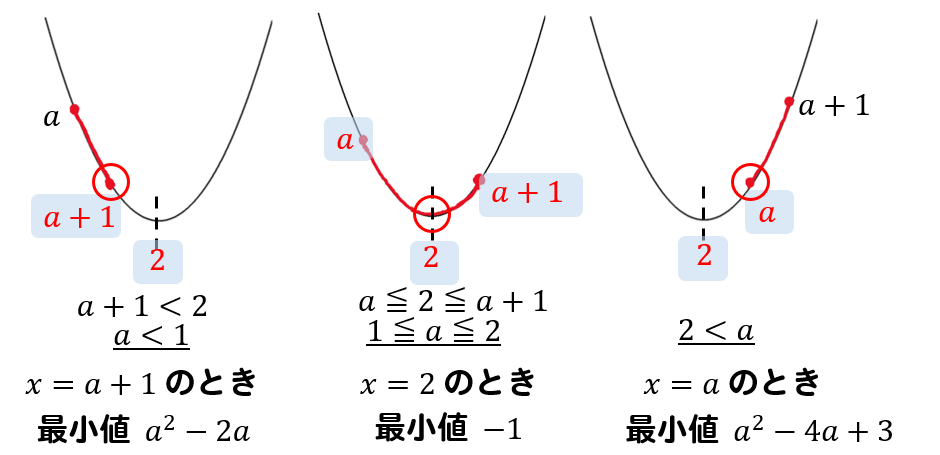
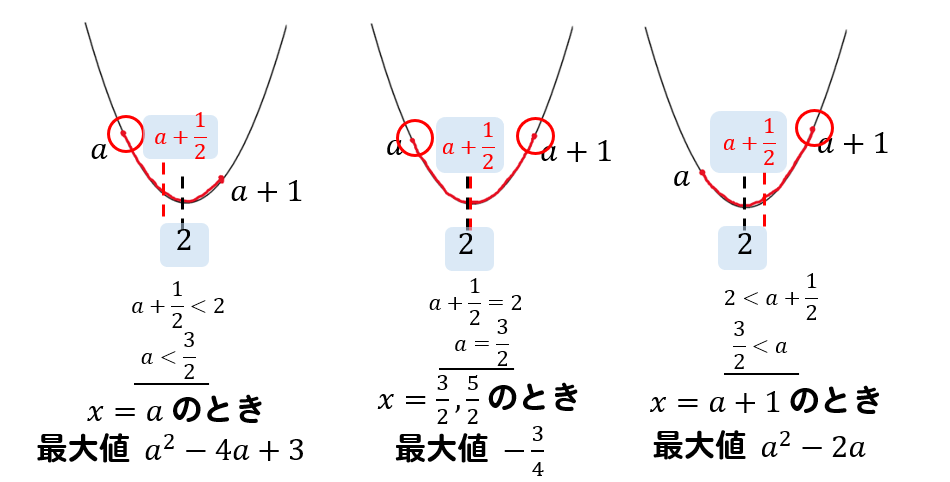
関数\(y=x^2-4x+3 (a≦x≦a+1)\) の最大値と最小値、およびそのときの\(x\)の値を求めなさい。
追加演習を用意しました!
場合分けの練習をもっとやりたい!という方に向けて追加演習を用意しました。
動画を見ながら一緒に解いてみてください^^
講義資料は無料のメルマガ講座内でお渡ししているので、こちらからお受け取りくださいね!
《最大値の場合分け》
《最小値の場合分け》
《最大・最小からグラフをかく》
二次関数の最大最小の場合分けまとめ!
お疲れ様でした!
二次関数の最大最小の場合分けは手間がかかる(^^;)
だけど、そんなに難しいことをやっているわけではありません。
しっかりと場合分けのパターンを身につけてしまえば楽勝です!


上に凸のグラフを扱う場合には
場合分けのパターンが下に凸とは逆になってしまうので気を付けてくださいね。
上に凸の最大値は下に凸の最小値と同じ考え方、最小値は下に凸の最大値と同じ考え方です。
以上!
- 一次関数の定義域、値域とは?問題の解き方を解説!
- 頂点の求め方、公式は?問題を使ってイチから解説!
- 平方完成!分数でくくるパターンの問題の解き方を解説!
- 平方完成!文字を含む式の場合は?やり方を丁寧に解説!
- 二次関数グラフの書き方を初めから解説!
- 二次関数の式の作り方をパターン別に解説!
- 二次関数を対称移動したときの式の求め方を解説!
- 平行移動したものが2点を通る式を作る方法とは?
- どのように平行移動したら重なる?例題を使って問題解説!
- 二次関数の最大・最小の求め方をイチから解説していきます!
- 場合分け!最大最小の応用問題の解き方をイチから解説! ←今回の記事
- 2変数関数の最大・最小の求め方、パターン別の解説!
- 二次関数の文章題!高校で学習する問題をパターン別まとめ!
- 分数、小数、ルートを含む二次方程式の解き方まとめ!
- 高校数学で学習する連立方程式の解き方まとめ!
- 文字係数の方程式の解き方まとめ!
- 判別式Dを使って解の個数を調べてみよう!
- 2次方程式の共通解、kの値の求め方はどうやる??
- x軸との共有点、グラフの位置関係を考える問題を解説!
- 係数の符号の決定、グラフから符号を決めるポイントを解説!
- x軸から切り取る線分の長さの求め方と公式!
- 放物線と直線の交点の求め方!
- 二次不等式の解き方を簡単に!高校数学をマスターしよう!
- 文字係数の2次不等式の解き方!場合分けの考え方は??
- 解からの係数決定!グラフの形と座標に注目せよ!
- 絶対不等式!パターン別の例題を使って解き方を解説!
- 2次方程式の解の存在範囲!判・軸・端の条件を見極めるのが重要!
- 4次不等式の解き方を例題解説!
- f(x) > g(x)となる範囲「すべての」「ある」の違いを理解しておこう!
- 絶対値のついたグラフを書いてみよう!


















すっっごく分かりやすいです‼️この場合分けが最初ちんぷんかんぷんで明日テストなのにどうしようと思っていたところでこのサイトに出会いました!!!突然めっちゃ解けるようになりました!!あまりにも感動したのでついコメント書いちゃいました✨ありがとうございます!!!!!
嬉しいコメントありがとうございます^^
テスト上手くいっているといいな~!!
これからもたくさん記事、動画をつくっていくので
引き続き参考にしてもらえると嬉しいです!