【文字係数の方程式】解き方の解説、練習問題をやってみよう！

高校数学Ⅰで学習する方程式の単元から

「文字係数の方程式」

について解説していきます。

文字係数の方程式とは次のような問題です。

【問題】

次の $x$ についての方程式を解け。$a$ は定数とする。

（1）$ax+2=x+a^2$

（2）$x^2-2x-a^+1=0$

（3）$ax^2+x-a=0$

(1)(3)のように最高次数の係数が文字のときには場合分けを利用する。

(2)はたすき掛けを上手く利用する。

ということになります。

では、それぞれの問題の解き方について確認しておきましょう。

記事の最後には練習問題を用意しているので、そこで理解度を深めていくことにしましょう。

Contents

文字係数の一次方程式（1）場合分け
文字係数の二次方程式（1）たすき掛け
文字係数の二次方程式（2）場合分け
練習問題に挑戦！
まとめ！

文字係数の一次方程式（1）場合分け

次の $x$ についての方程式を解け。$a$ は定数とする。

（1）$ax+2=x+a^2$

一次方程式を解くためには、最終的に$x$の係数で割る必要が出てきますね。

$$Ax=B ⇒ x=\frac{B}{A}$$

しかし、$x$の係数が0だった場合…

0で割ることはできませんので、$x=\frac{B}{A}$ の形が作れないことになってしまいます。

そこで、場合分けをしていくことになるのです。

$x$の係数が0にならない場合　⇒　割って $x=\frac{B}{A}$ としてOK。

$x$の係数が0になる場合　⇒　割れないので違うアプローチをする。

では、解法の手順を確認しておきましょう。

$$\begin{eqnarray}ax+2&=&x+a^2\\[5pt]ax-x&=&a^2-2\\[5pt](a-1)x&=&a^2-2 \end{eqnarray}$$

$x$の係数が $(a-1)$ であることが分かります。

これが0にならない、0になる場合で分けて考えていきましょう。

$a-1≠0$ ⇒ $a≠1$ のとき

$(a-1)$ で割ることができるので

$$\begin{eqnarray}(a-1)x&=&a^2-2\\[5pt]x&=&\frac{a^2-2}{a-1} \end{eqnarray}$$

$a-1=0$ ⇒ $a=1$ のとき

もとの方程式に $a=1$ を代入すると

$$\begin{eqnarray}(1-1)x&=&1^2-2\\[5pt]0\cdot x&=&-1 \end{eqnarray}$$

となります。

このとき左辺は、$x$がどんな値であっても0になってしまいます。

すると右辺の$-1$ と等しくなることはあり得ませんね。

よって、この等式を満たす$x$ はない。

解なし！となります。

以上のことをまとめると、

答え

$a≠1$ のとき $x=\frac{a^2-2}{a-1}$

$a=1$ のとき解なし

ポイント！

$x$ の係数が0の場合には割り算ができない。

なので、場合分けが必要になる。

文字係数の二次方程式（1）たすき掛け

次の $x$ についての方程式を解け。$a$ は定数とする。

（2）$x^2-2x-a^+1=0$

この問題では、最高次数$x^2$ の係数は文字ではありません。

そのため、場合分けを考える必要はありません。

まずは因数分解ができないか考える。

因数分解ができないようであれば解の公式を使って二次方程式を解いていきます。

この問題では、ちょっとイメージしずらいかもしれませんが

このようにたすき掛けで因数分解することができます。

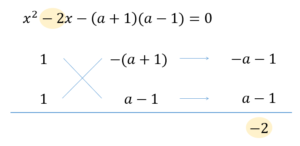
$$\begin{eqnarray}x^2-2x-a^+1&=&0\\[5pt]x^2-2x-(a^2-1)&=&0\\[5pt]x^2-2x-(a+1)(a-1)&=&0\\[5pt]\{x-(a+1)\}\{x+(a-1)\}&=&0\\[5pt]x=a+1, -a+1&& \end{eqnarray}$$

答え

$$x=a+1, -a+1$$

ポイント！

最高次数の係数が文字ではないので、場合分けは不要。

まずは因数分解を試してみる。

できないようであれば解の公式を用いて解を求める。

文字係数の二次方程式（2）場合分け

次の $x$ についての方程式を解け。$a$ は定数とする。

（3）$ax^2+x-a=0$

この問題はちょっとイジワル要素が含まれています。

問題文には「 $x$ についての方程式」としか書かれていません。

ということは、この方程式は

$x^2$ の係数が0であり「一次方程式」となる。

$x^2$ の係数が0ではなく「二次方程式」となる。

この2パターンが考えられます。

それぞれの方程式では解き方が異なるため、場合分けをして考えてく必要があります。

$a=0$ のとき（一次方程式になるパターン）

$$\begin{eqnarray}0\cdot x^2+x-0&=&0\\[5pt]x&=&0 \end{eqnarray}$$

$a≠0$ のとき（二次方程式になるパターン）

$ax^2+x-a=0$ は二次方程式であり、因数分解ができそうにないので解の公式を利用していきます。

$$\begin{eqnarray}x&=&\frac{-1\pm\sqrt{1^2-4\cdot a\cdot(-a)}}{2a}\\[5pt]&=&\frac{-1\pm\sqrt{4a^2+1}}{2a} \end{eqnarray}$$

解の公式を利用した場合には、ちゃんとルートの中身が0以上であることを確認しておきましょう。

もしも、ルートの中身が負になってしまえば「実数解なし」になります。

今回は、$4a^2+1>0$ となっているので、解として適していることが分かります。

したがって、以上のことをまとめると

答え

$a=0$ のとき $x=0$

$a≠0$ のとき $x=\frac{-1\pm\sqrt{4a^2+1}}{2a}$

ポイント！

$x^2$ の係数が文字の場合

一次方程式、二次方程式になる場合で分けて考えていきましょう！

練習問題に挑戦！

【問題】

次の $x$ についての方程式を解け。$a$ は定数とする。

（1）$(a^2-2a)x=a-2$

（2）$x^2+ax-a-1=0$

（3）$(a-1)x^2-2(a-2)x-2=0$

解説＆答えはこちら

答え

（1）

$a≠0$ かつ $a≠2$ のとき $x=\frac{1}{a}$

$a=0$ のとき解なし

$a=2$ のとき解はすべて実数

（2）$x=1, -a-1$

（3）

$a=1$ のとき $x=1$

$a≠1$ のとき $x=\frac{a-2\pm\sqrt{a^2-2a+2}}{a-1}$

（1）

$$\begin{eqnarray}(a^2-2a)x&=&a-2\\[5pt]a(a-2)x&=&a-2 \end{eqnarray}$$

$a(a-2)≠0$ ⇒ $a≠0$ かつ $a≠2$ のとき

$$\begin{eqnarray}a(a-2)x&=&a-2\\[5pt]x&=&\frac{a-2}{a(a-2)}\\[5pt]x&=&\frac{1}{a} \end{eqnarray}$$

$a(a-2)=0$ ⇒ $a=0$ または $a=2$

$a=0$ のとき

$$\begin{eqnarray}0\cdot x&=&-2 \end{eqnarray}$$

これを満たす$x$ はないので、解なし。

$a=2$ のとき

$$\begin{eqnarray}0\cdot x&=&0 \end{eqnarray}$$

どんな$x$ でも成り立つので、解はすべての数。

（2）

$$\begin{eqnarray}x^2+ax-a-1&=&0\\[5pt]x^2+ax-(a+1)&=&0\\[5pt]\{x+(a+1)\}(x-1)&=&0 \\[5pt]x=-a-1,1&&\end{eqnarray}$$

（3）

$a-1=0$ ⇒ $a=1$ のとき

$$\begin{eqnarray}2x-2&=&0\\[5pt]x&=&1 \end{eqnarray}$$

$a-1≠0$ ⇒ $a≠1$ のとき

$(a-1)x^2-2(a-2)x-2=0$ において解の公式を利用すると

$$\begin{eqnarray}x&=&\frac{2(a-2)\pm\sqrt{4(a-2)^2-4(a-1)\cdot(-2)}}{2(a-1)}\\[5pt]&=&\frac{a-2\pm\sqrt{a^2-2a+2}}{a-1} \end{eqnarray}$$

$a^2-2a+2=(a-1)^2+1>0$ より、これは解として適している。

まとめ！

お疲れ様でした！

「文字で割るときは注意」

文字が0になる場合には割ることができなくなってしまいます。

そのことを考慮して、最高次数の係数が文字のときには場合分けをするようにしましょう。

また、問題文にしっかりと目を通すようにしてください。

「方程式」としか書かれていない場合には、

一次、二次方程式になるそれぞれのパターンを考える必要が出てきますね。

こちらの記事も合わせてどうぞ！

文字係数の一次方程式（1）場合分け

文字係数の二次方程式（1）たすき掛け

文字係数の二次方程式（2）場合分け

練習問題に挑戦！

まとめ！

コメントを残す コメントをキャンセル

RECOMMENDこちらの記事も人気です。

【苦手な人向け】二次関数の最大・最小の求め方をイチから解説していきます！

高校数学で学習する連立方程式の解き方まとめ！

分数、小数、ルートを含む二次方程式の解き方まとめ！

【苦手な人向け】絶対値のついたグラフを書いてみよう！

二次関数の文章題！高校で学習する問題をパターン別まとめ！

【平方完成】文字を含む式の場合は？やり方を丁寧に解説！

【二次関数】x軸から切り取る線分の長さの求め方と公式！

2次方程式の共通解、kの値の求め方はどうやる？？

コメントを残すコメントをキャンセル