高校数学Ⅰで学習する2次関数の単元から
「2次方程式の解の存在範囲」
について解説していきます。
- 異なる2つの正の解をもつ。
- 符号が異なる2つの解をもつ。
- 1と2の間に異なる2つの解をもつ。
などなど。
このように解の存在範囲から定数 \(a\) の値の範囲を求めていく問題の解き方についてまとめていきます。
この問題を考える上で大事なポイントは、
2次関数のグラフとして考え、
「判別式」「軸」「区間の端点の\(y\)座標」
この3点に着目して、条件を作っていくことです。
これら3つのポイントを省略して「判・軸・端」と呼んで覚えておくと便利です。
では、パターンごとに問題の解き方を解説していきます。
今回の内容はこちらの動画でも解説しています。
サクッと理解したい方はこちらをどうぞ(‘◇’)ゞ
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
2次方程式の解の存在範囲
【問題】
\(x\) についての2次方程式 \(x^2-2ax-a+2=0\) が次のような解をもつとき,定数 \(a\) の値の範囲を求めよ。
(1)異なる2つの正の解
(2)異なる2つの負の解
(3)符号が異なる2つの解
\(x\) についての2次方程式 \(-x^2+(m-10)x-m-14=0\) が次のような解をもつとき,定数 \(m\) の値の範囲を求めよ。
(4)異なる2つの解がともに1より大きくなる。
\(x\) についての2次方程式 \(x^2+kx+2k-1=0\) が次のような解をもつとき,定数 \(k\) の値の範囲を求めよ。
(5)異なる2つの解が \(-2\) と \(5\) の間にある。
\(x\) についての2次方程式 \(x^2+(a-1)x-a^2+2=0\) が次のような解をもつとき,定数 \(a\) の値の範囲を求めよ。
(6)1つの解が \(-2\) と \(0\) の間にあり,他の解が \(0\) と \(1\) の間にある。
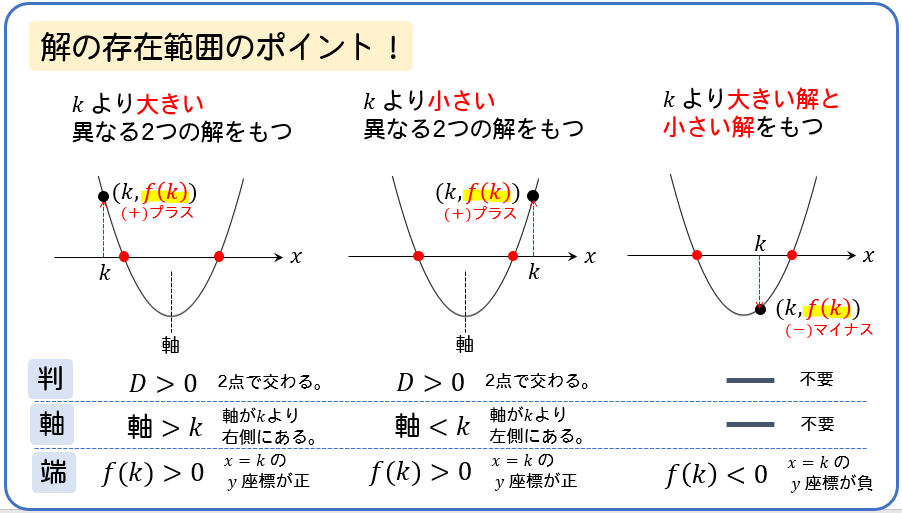


これらの条件は丸暗記するのではなく、グラフのイメージ図をかいて自分で読み取れるようにしておきましょう。
(1)異なる2つの正の解
\(x\) についての2次方程式 \(x^2-2ax-a+2=0\) が次のような解をもつとき,定数 \(a\) の値の範囲を求めよ。
(1)異なる2つの正の解
まずは、異なる2つの正の解をもつような放物線のグラフをかいてみましょう。
区間の端点は \(x=0\) のところであり、「判・軸・端」の3つの条件が作れますね。
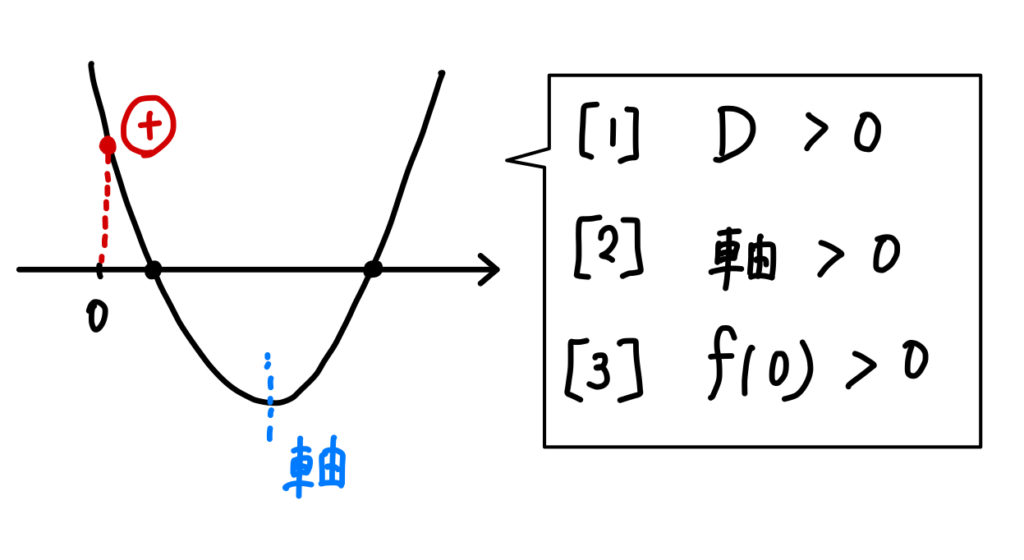
条件を作ることができたら、それぞれの条件から \(a\) の範囲を求め、最後に共通部分をとっていきましょう。

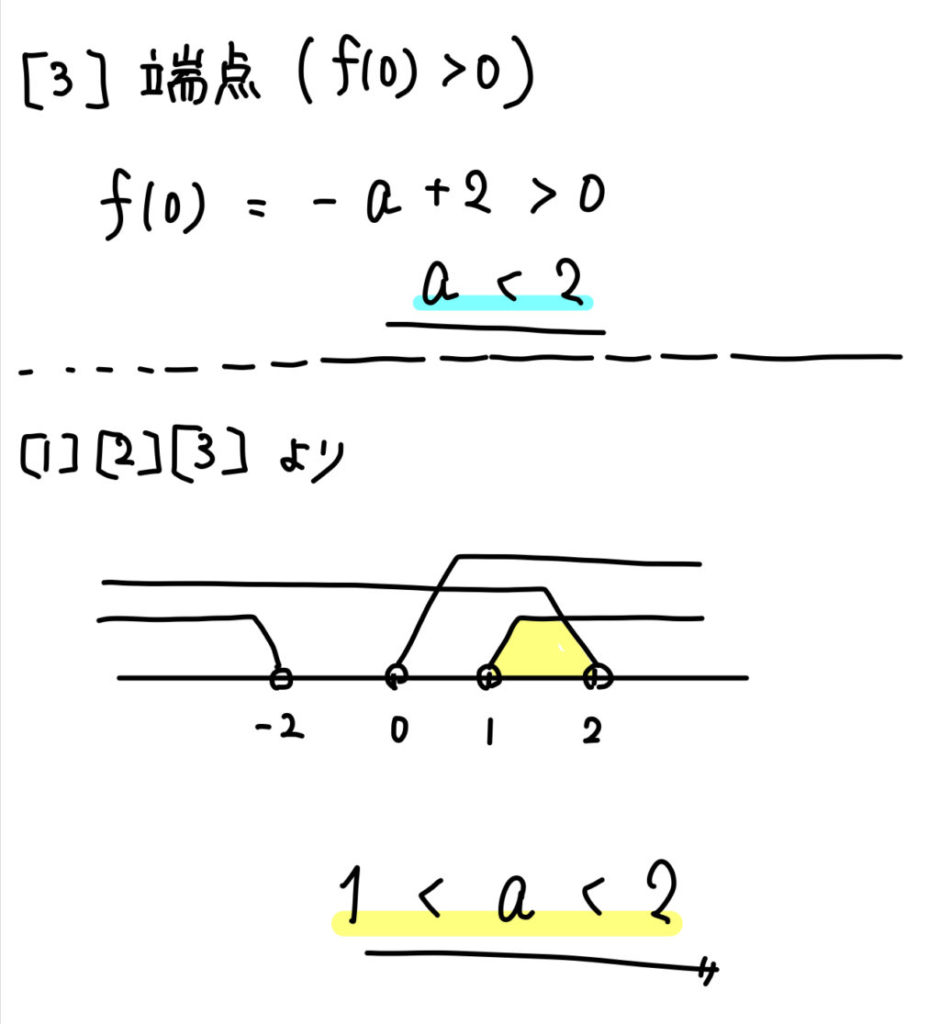
(2)異なる2つの負の解
\(x\) についての2次方程式 \(x^2-2ax-a+2=0\) が次のような解をもつとき,定数 \(a\) の値の範囲を求めよ。
(2)異なる2つの負の解
こちらもイメージ図をかいて考えていきます。
すると、次のような条件を作ることができます。

(1)とは、軸の正負が変わっただけですね。

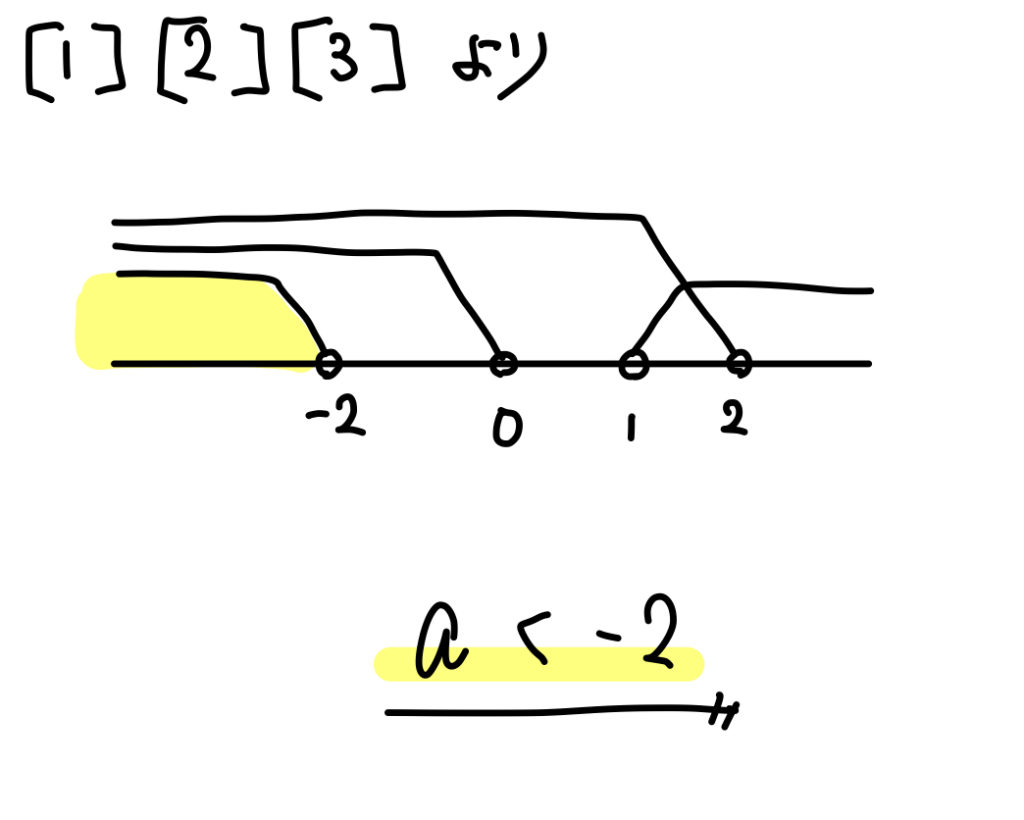
よって、このように範囲を求めることができました。
(3)符号が異なる2つの解
\(x\) についての2次方程式 \(x^2-2ax-a+2=0\) が次のような解をもつとき,定数 \(a\) の値の範囲を求めよ。
(3)符号が異なる2つの解
区間の端点をはさみこむように解が存在する場合、これはラッキー問題となります!
通常であれば「判・軸・端」の3つの条件を考える必要があるのですが、今回のように端点をはさみこむ場合には「端」のみを考えればOKとなります。
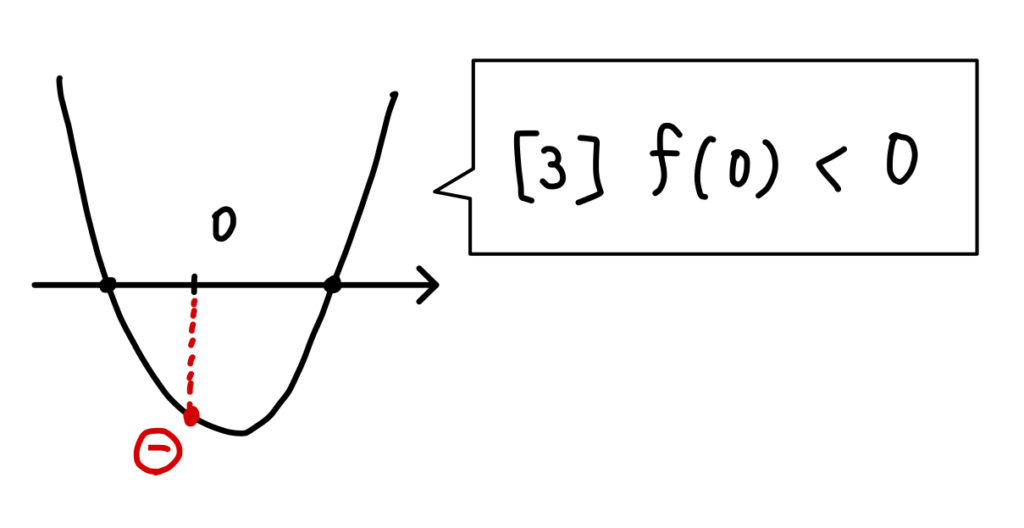
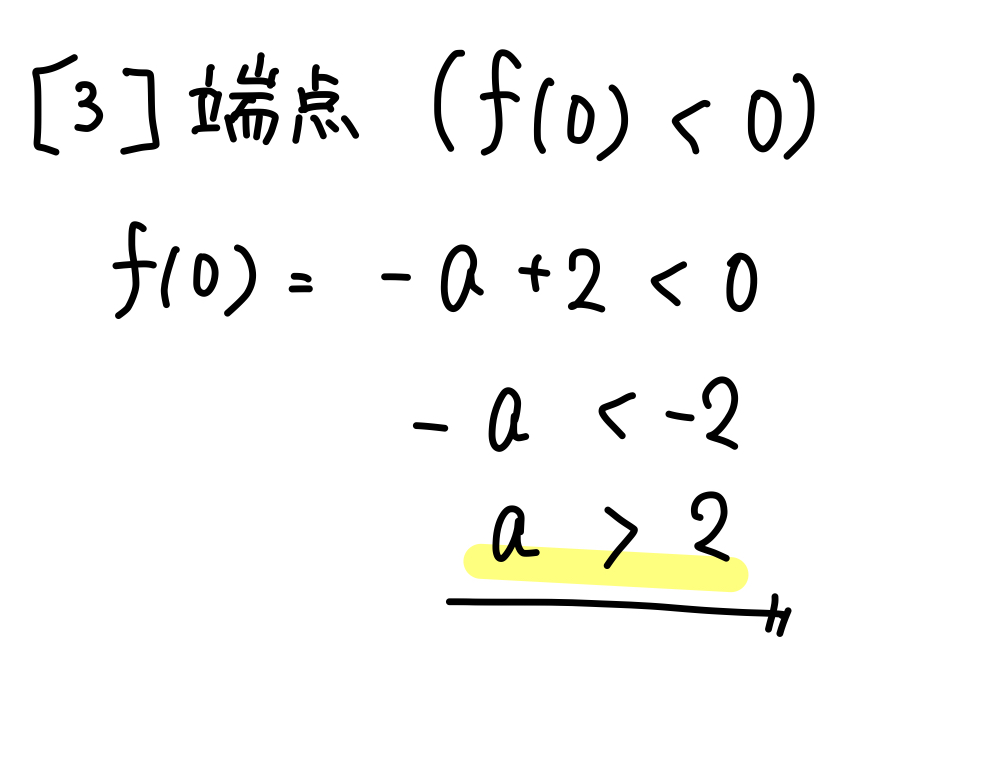
(4)異なる2つの解がともに1より大きくなる。
\(x\) についての2次方程式 \(-x^2+(m-10)x-m-14=0\) が次のような解をもつとき,定数 \(a\) の値の範囲を求めよ。
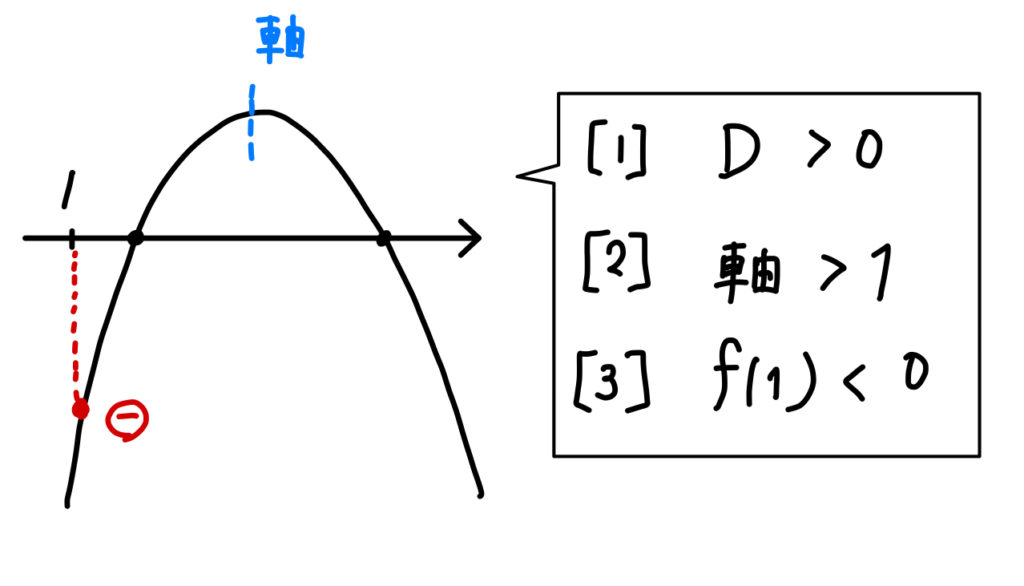
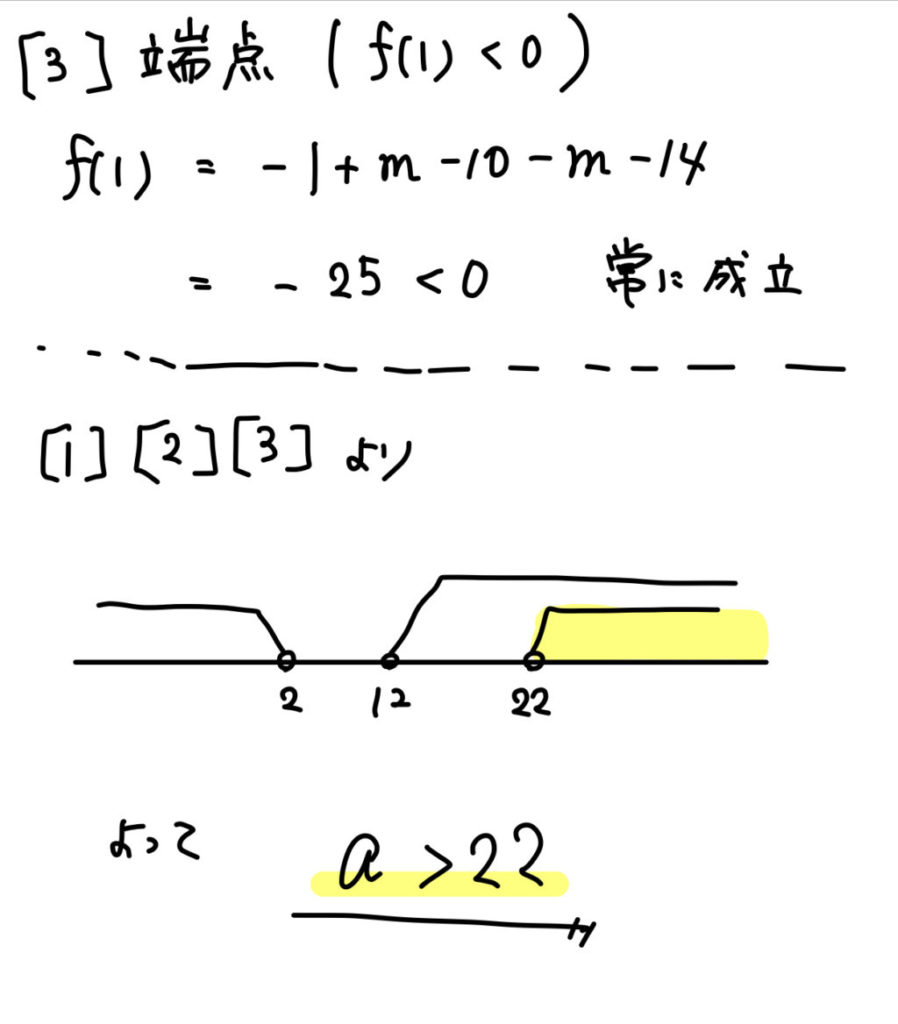
(4)異なる2つの解がともに1より大きくなる。
こちらもイメージ図をかいて考えましょう。
今回は区間の端点が \(x=1\) となっていることを踏まえて、3つの条件を作っていきます。

(5)異なる2つの解が \(-2\) と \(5\) の間にある。
\(x\) についての2次方程式 \(x^2+kx+2k-1=0\) が次のような解をもつとき,定数 \(k\) の値の範囲を求めよ。
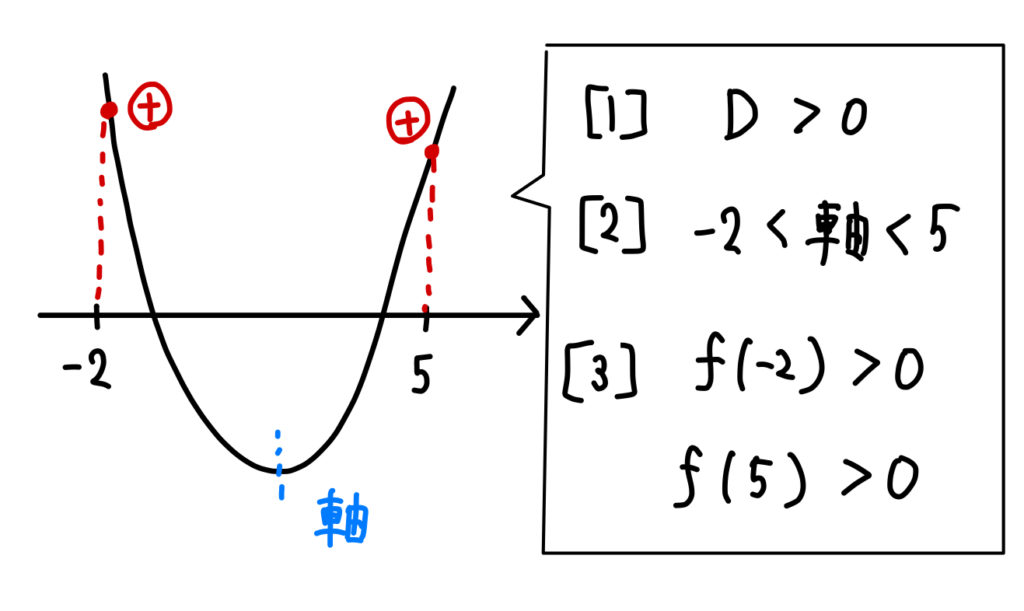
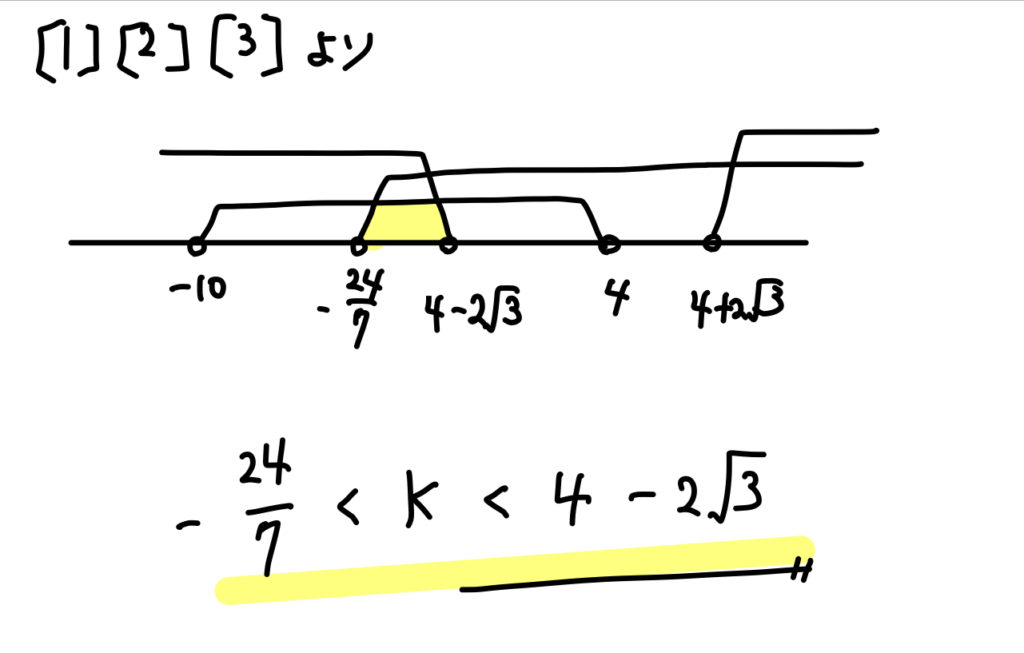
(5)異なる2つの解が \(-2\) と \(5\) の間にある。
端点が\(-2\)、\(5\) のの2つあることに注意して3つの条件を作っていきましょう。
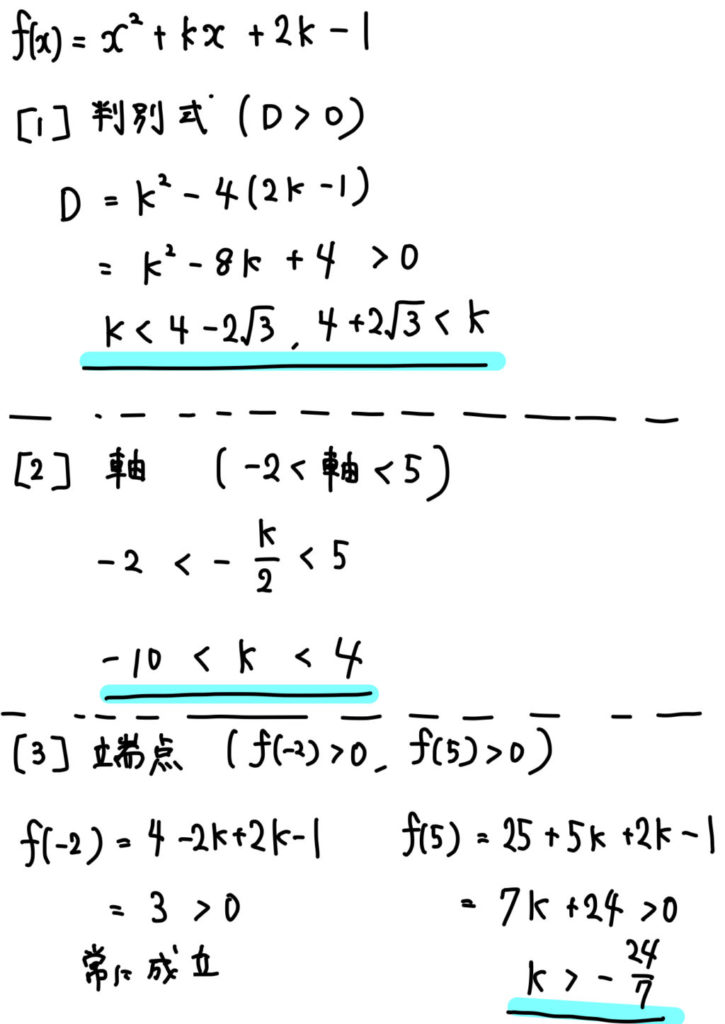
(6)1つの解が \(-2\) と \(0\) の間にあり,他の解が \(0\) と \(1\) の間にある。
\(x\) についての2次方程式 \(x^2+(a-1)x-a^2+2=0\) が次のような解をもつとき,定数 \(a\) の値の範囲を求めよ。
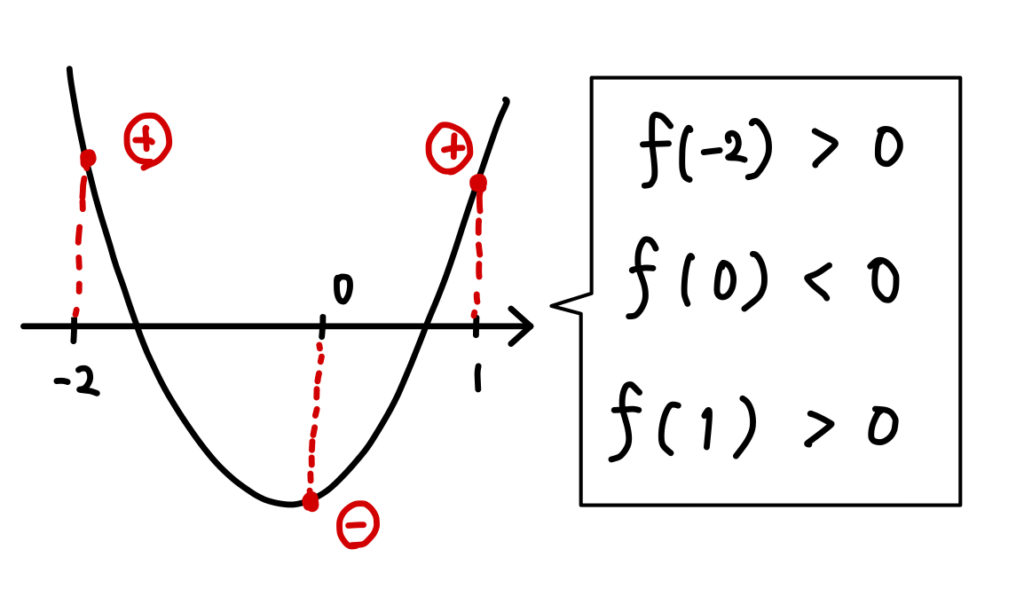
(6)1つの解が \(-2\) と \(0\) の間にあり,他の解が \(0\) と \(1\) の間にある。
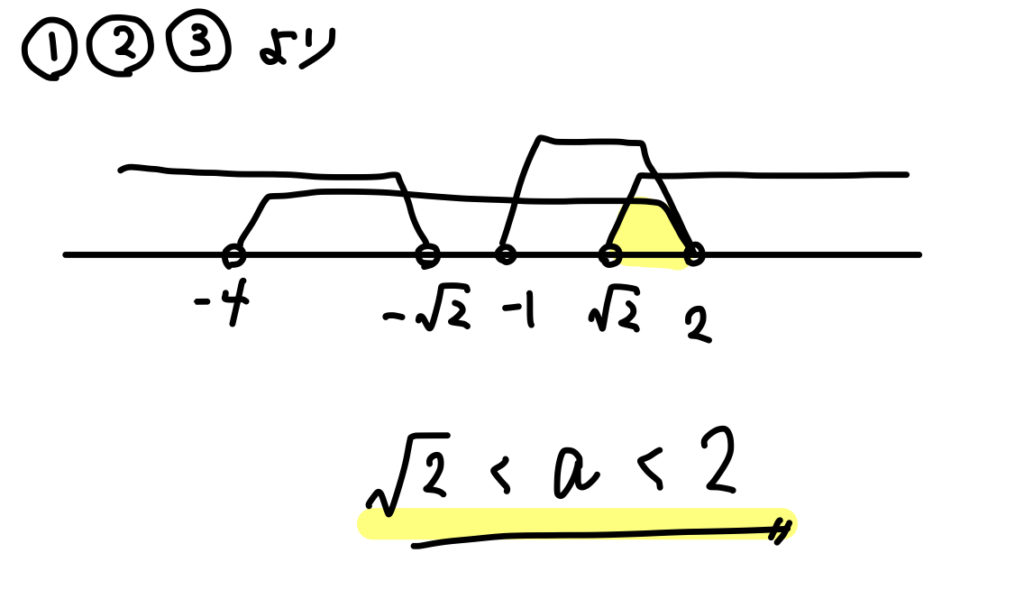
2つの解が、どこの間にあるかを具体的に指定されている場合、次のように端点の符号から条件を作っていきましょう。
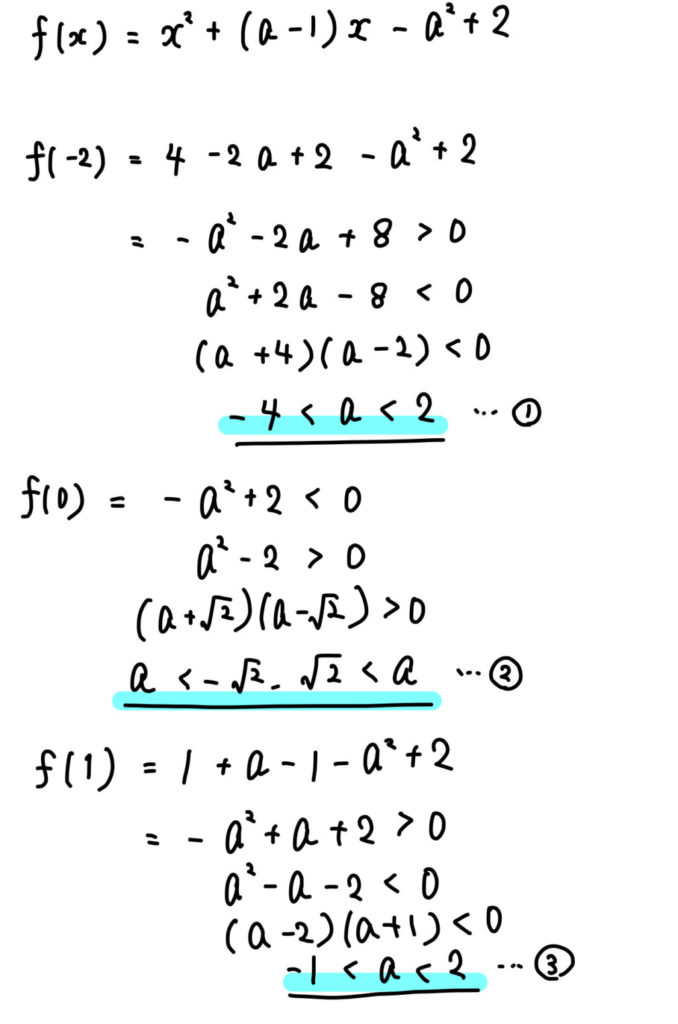
まとめ!
お疲れ様でした!
2次方程式の解の存在範囲は、入試でも頻出の問題です。
冒頭でも述べましたが、大事なポイントは「判・軸・端」です。
イメージ図のグラフをかいて、3つの条件をチェックしていくようにしましょう(/・ω・)/
- 一次関数の定義域、値域とは?問題の解き方を解説!
- 頂点の求め方、公式は?問題を使ってイチから解説!
- 平方完成!分数でくくるパターンの問題の解き方を解説!
- 平方完成!文字を含む式の場合は?やり方を丁寧に解説!
- 二次関数グラフの書き方を初めから解説!
- 二次関数の式の作り方をパターン別に解説!
- 二次関数を対称移動したときの式の求め方を解説!
- 平行移動したものが2点を通る式を作る方法とは?
- どのように平行移動したら重なる?例題を使って問題解説!
- 二次関数の最大・最小の求め方をイチから解説していきます!
- 場合分け!最大最小の応用問題の解き方をイチから解説!
- 2変数関数の最大・最小の求め方、パターン別の解説!
- 二次関数の文章題!高校で学習する問題をパターン別まとめ!
- 分数、小数、ルートを含む二次方程式の解き方まとめ!
- 高校数学で学習する連立方程式の解き方まとめ!
- 文字係数の方程式の解き方まとめ!
- 判別式Dを使って解の個数を調べてみよう!
- 2次方程式の共通解、kの値の求め方はどうやる??
- x軸との共有点、グラフの位置関係を考える問題を解説!
- 係数の符号の決定、グラフから符号を決めるポイントを解説!
- x軸から切り取る線分の長さの求め方と公式!
- 放物線と直線の交点の求め方!
- 二次不等式の解き方を簡単に!高校数学をマスターしよう!
- 文字係数の2次不等式の解き方!場合分けの考え方は??
- 解からの係数決定!グラフの形と座標に注目せよ!
- 絶対不等式!パターン別の例題を使って解き方を解説!
- 2次方程式の解の存在範囲!判・軸・端の条件を見極めるのが重要! ←今回の記事
- 4次不等式の解き方を例題解説!
- f(x) > g(x)となる範囲「すべての」「ある」の違いを理解しておこう!
- 絶対値のついたグラフを書いてみよう!


















コメントを残す