【連立方程式】代入法の解き方をわかりやすく問題を使って徹底解説！

今回は中２で学習する

『連立方程式』の単元から

連立方程式を代入法で解く方法について解説していくよ！

連立方程式を解くためには

『加減法』と『代入法』という2つの解き方があったよね。

でも…

加減法は分かるけど、代入法は苦手…

っていう人が多いんだよね。

代入法ってすっごく簡単なのに…

というわけで

今回は、この代入法について学習していきましょう！

今回の記事はこちらの動画でも解説しています(/・ω・)/

代入法とは？？

加減法は式を足したり、引いたりしながら解いていく方法でした。

一方、代入法はというと

代入しながら解く！

そのまんま…笑

連立方程式が次のように

$$\LARGE{\begin{eqnarray} \left\{ \begin{array}{l} y =3x +1 \\ 5x – y = 1 \end{array} \right. \end{eqnarray}}$$

$$\LARGE{\begin{eqnarray} \left\{ \begin{array}{l} x=y +5 \\x =4y+11 \end{array} \right. \end{eqnarray}}$$

連立されている式が

\(x=…\)や\(y=…\)のようになっていて

いつものように\(x\)と\(y\)が

左辺に揃っていないようなときには

代入法を使うと楽に計算できるサインです。

それでは、代入法を使って解く問題を

パターン別になるべくわかりやすく解説していから

がんばって勉強していこー！

代入法で解く問題をパターン別に解説！

それでは、代入法の問題を3つのパターンに分けて解説していきます。

• 基本パターン
• \(y=… , y=…\)パターン
• 係数ごと代入しちゃうパターン

代入法の基本パターン

次の方程式を解きなさい。

$$\LARGE{\begin{eqnarray} \left\{ \begin{array}{l} y =x -9 \\ 2x -5 y = 3 \end{array} \right. \end{eqnarray}}$$

この連立方程式のように

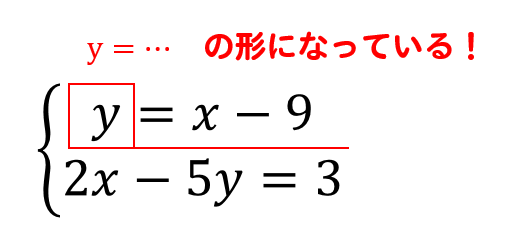
となっていれば、代入法のサインです！

\(y=…\)となっている式にかっこをつけて

もう一方の式の\(y\)の部分に代入してやります。

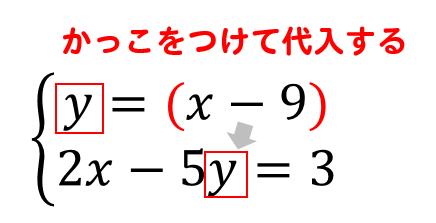
すると、次のような式にまとめてやることができます。

$$\LARGE{2x-5(x-9)=3}$$

そうすれば、あとは計算していくだけです。

$$\LARGE{2x-5(x-9)=3}$$

$$\LARGE{2x-5x+45=3}$$

$$\LARGE{2x-5x=3-45}$$

$$\LARGE{-3x=-42}$$

$$\LARGE{x=14}$$

\(x\)の値が求まれば

\(y =x -9\)か\(2x -5 y = 3\)のどちらかの式に代入してやります。

ほとんどの場合が\(x=…, y=…\)となっている式に代入する方が楽なので

今回も\(y =x -9\)に代入していきます。

すると

$$\LARGE{y=14-9=5}$$

となり

この連立方程式の答えは

$$\LARGE{\begin{eqnarray} \left\{ \begin{array}{l} x=14  \\ y = 5 \end{array} \right. \end{eqnarray}}$$

代入法の手順としては

至ってシンプル！

かっこをつけずに代入しちゃうと

符号ミスやかけ算忘れにつながるから

そこは気を付けておこうね！

\(y=… , y=…\)パターン

次の方程式を解きなさい。

$$\LARGE{\begin{eqnarray} \left\{ \begin{array}{l} y =3x -1 \\  y =x+ 5 \end{array} \right. \end{eqnarray}}$$

式が両方とも\(y=…, y=…\)となっているパターンの問題を考えてみましょう。

このパターンの連立方程式は

一次関数の単元で多く利用することになります。

ただ、見た目はちょっと違いますが

解き方は基本パターンと同じです。

式にかっこをつけて

もう一方の式に代入します。

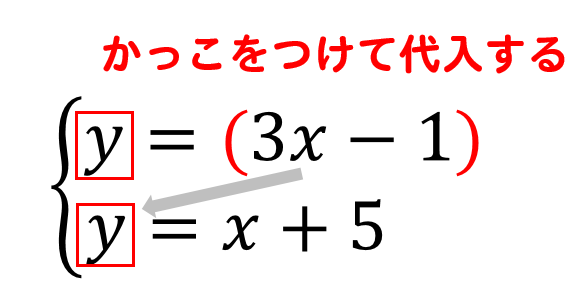
すると

$$\LARGE{3x-1=x+5}$$

$$\LARGE{3x-x=5+1}$$

$$\LARGE{2x=6}$$

$$\LARGE{x=3}$$

\(x\)の値が求まれば

\(y=3x-1\)、\(y=x+5\)のどちらかの式に代入します。

今回は\(y=3x-1\)に代入して計算していくと

$$\LARGE{y=3\times 3 -1}$$

$$\LARGE{y=8}$$

よって、答えは

$$\LARGE{\begin{eqnarray} \left\{ \begin{array}{l} x=3  \\ y = 8 \end{array} \right. \end{eqnarray}}$$

\(y=…, y=…\)となっているパターンでも

解き方は一緒でしたね！

見た目に騙されないでください。

係数ごと代入しちゃうパターン

次の方程式を求めなさい。

$$\LARGE{\begin{eqnarray} \left\{ \begin{array}{l} 4x +3y=7  \\  3y =-7x+ 10 \end{array} \right. \end{eqnarray}}$$

あれ！？

\(3y=…\)ってどうすんの！？

\(y=…\)の式に3がくっついているので

いつもと違って困っちゃいますね…

そういうときは

慌てず、もう一方の式を見てみましょう。

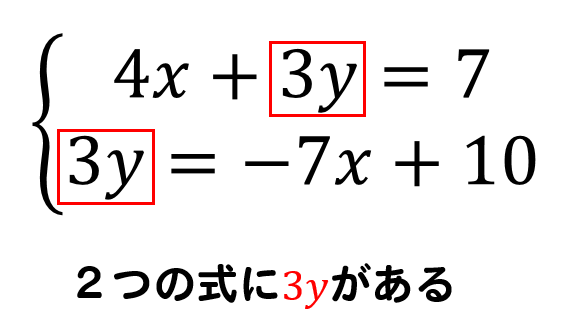
そうすると、邪魔だと思っていた\(3y\)が

もう一方の式にもあるのがわかりますね。

こういうときには

\(3y\)に式をまるごと代入してやります。

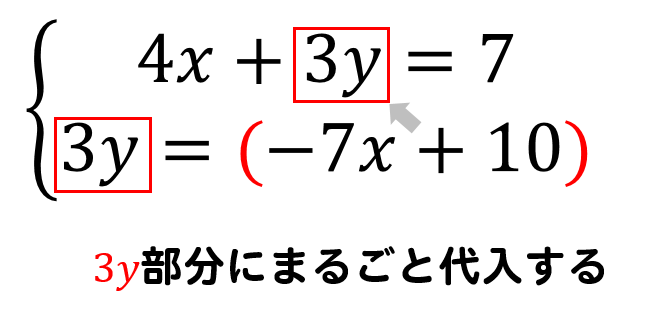
すると、式は

$$\LARGE{4x+(-7x+10)=7}$$

となります。

あとは計算していきます。

$$\LARGE{4x-7x+10=7}$$

$$\LARGE{-3x=7-10}$$

$$\LARGE{-3x=-3}$$

$$\LARGE{x=1}$$

\(x\)の値が求まれば

\(3y=-7x+10\)に代入します。

$$\LARGE{3y=-7\times 1 +10}$$

$$\LARGE{3y=-7 +10}$$

$$\LARGE{3y=3}$$

$$\LARGE{y=1}$$

答えは

$$\LARGE{\begin{eqnarray} \left\{ \begin{array}{l} x=1  \\ y = 1 \end{array} \right. \end{eqnarray}}$$

となりました。

\(x=…, y=…\)の式に何か数がくっついている場合は

もう一方の式にも同じものがないか探してみましょう。

同じものがあれば

その部分にまるごと式を代入してやればOKです。

それでは、いくつか練習問題に挑戦して

理解を深めていきましょう！

演習問題で理解を深める！

【追加演習】文章題のための計算特訓にチャレンジ！

さぁ、ここまでのところで加減法、代入法をクリアして、連立方程式の基本計算はバッチリになったかと思います！

次のステップではいよいよ文章題に入っていくのですが…ここでちょっと厄介な問題点があります。

それは…文章題の計算ややこしすぎなんだけどぉ！！ってことです(^^;)

文章題になると小数、分数、かっこを含む計算が多発します。

せっかく読解して式が作れたのに、その計算がクリアできずに点がとれない…というすっごくもったいない状況になるので、ややこしい計算にもスラスラ対処できるように練習しといてもらいたいです！

というわけで、文章題の中で出てくる計算を8つ取り上げてみました。

すべて入試問題からピックアップしてみました！これが全部解ければ文章題への準備はバッチリ！

というわけで、これらの演習問題＆解説をプリント形式で用意しているので、印刷してお子さんに渡してあげてください。

ややこしい部分は動画解説を参考にしながらがんばってください＾＾

追加演習をやってテストの点数をUPさせたい方には、課題プリントをメールで送らせてもらっています。

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

代入法の解き方　まとめ

お疲れ様でした！

代入法の解き方は簡単だったね(^^)

慣れてくれば

加減法よりも式が少ないし

楽に感じるのではないかと思います。

関数の単元で、連立方程式が必要になる場合には

ほとんどが代入法で解いていくようになるから

しっかりと理解しておく必要があるね！

ファイトだー(/・ω・)/