今回は二次関数の単元から「係数の符号の決定」という問題について解説していきます。
符号の決定とは、次のような問題のことをいいます。
【問題】
二次関数\(y=ax^2+bx+c\) のグラフが下の図のようになっているとき、次の値の符号を求めなさい。
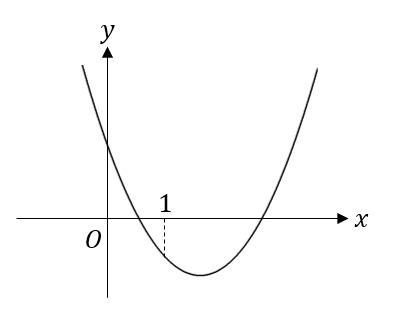
(1)\(a\) (2)\(b\) (3)\(c\) (4)\(b^2-4ac\) (5)\(a+b+c\) (6)\(a-b+c\)
グラフをどのように読み取れば、それぞれの係数の符号を決めることができるのか。
最初に結論をまとめてしまうと以下の通りです。
| \(a\)の符号 | グラフの上凸、下凸から判断する |
| \(b\)の符号 | 軸の位置から判断する |
| \(c\)の符号 | \(y\)軸との交点の座標から判断する |
| \(b^2-4ac\)の符号 | グラフの\(x\)軸との共有点の個数から判断する |
| \(a+b+c\)の符号 | \(x=1\) のときの\(y\)座標から判断する |
| \(a-b+c\)の符号 | \(x=-1\)のときの\(y\)座標から判断する |
それでは、それぞれのポイントと細かい解説をしていきます(^^)
今回の内容は動画でも解説しているので、サクッと理解したい方はこちらをどうぞ!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
符号の決定(\(a\)の考え方)
| \(a\)の符号 | グラフの上凸、下凸から判断する |
二次関数の式 \(y=ax^2+bx+c\) において、\(x^2\)の係数である\(a\)の符号はグラフの形によって決まります。
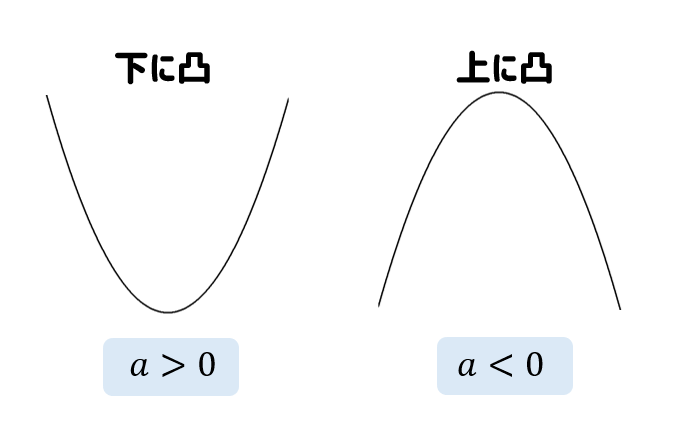
このように
上に凸の放物線であれば \(a>0\)
下に凸の放物線であれば \(a<0\) となります。
よって、今回の問題であれば
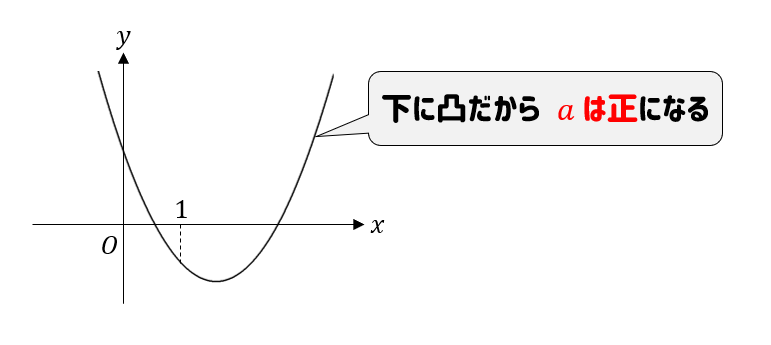
グラフは下に凸となっているので、\(a>0\) となります。
答え
$$a>0$$
符号の決定(\(b\)の考え方)
| \(b\)の符号 | 軸の位置から判断する |
\(b\)の符号を判断するためには、二次関数\(y=ax^2+bx+c\)の軸が\(\displaystyle{-\frac{b}{2a}}\) と表せることを知っておく必要があります。
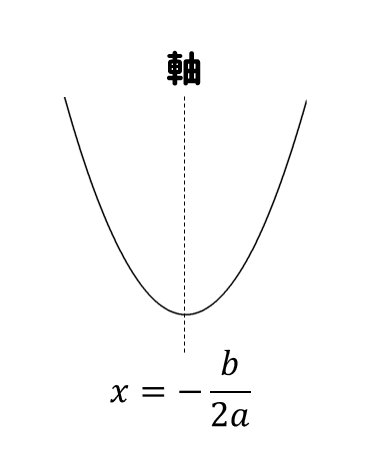
なんでこんな式になるんだっけ?と思った方は、\(y=ax^2+bx+c\) を平方完成して頂点を求めてみると上のような式になっていることを確かめれます。
だけど、計算が面倒なので…この式は覚えておいたほうがよいです(^^)
そして、この軸の式と用いて\(b\) の符号を決定していくんだけど、手順としては次の通りです。
まずは、軸の位置に注目。
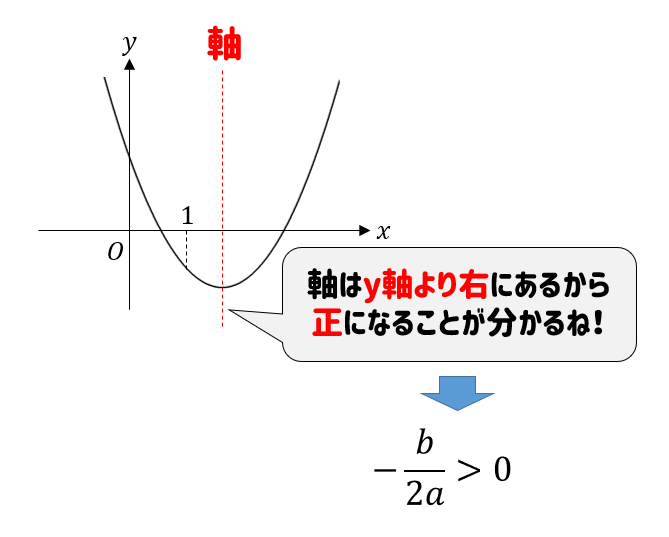
軸の符号を決定します。
次の(1)で求めた\(a\)に符号を取り入れて考えていきます。
今回の問題では \(a>0\) だったので
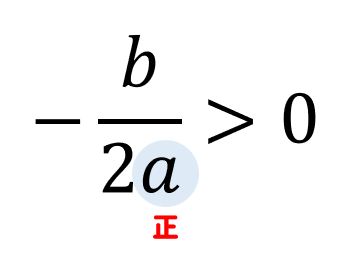
このように、\(2a\) は正になるということが分かります。
このことを頭に入れておいて、次の不等式を解いていきましょう。
$$\begin{eqnarray} -\frac{b}{2a}&>&0\\[5pt]-\frac{b}{2a}\times 2a&>&0\times 2a\\[5pt]-b&>&0\\[5pt]b&<&0\end{eqnarray}$$
よって、答えは\(b<0\) となります。
答え
$$b<0$$
符号の決定問題の中で、一番難しいのが\(b\)ですね(^^;)
まずは、軸の式\(x=-\frac{b}{2a}\) を覚えておくこと。
\(a\) の符号を考えながら不等式を解く必要があること。
この2点が慣れるまでは大変かと思います。
何度も練習して身につけていきましょう。
記事の最後には練習問題を用意しているのでご活用ください。
符号の決定(\(c\)の考え方)
| \(c\)の符号 | \(y\)軸との交点の座標から判断する |
\(c\)の符号はとっても簡単!
二次関数\(y=ax^2+bx+c\) において、\(x=0\) を代入したときの\(y\)座標が\(c\)です。
つまり、グラフでいうところの\(y\)軸との交点。
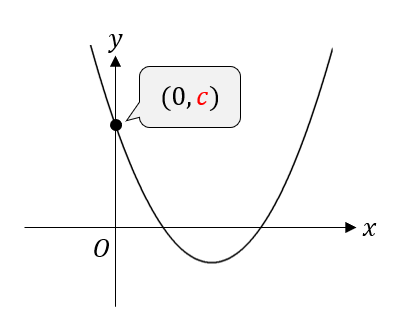
ここの符号を見れば、\(c\)の符号を判断することができます。
今回の問題であれば
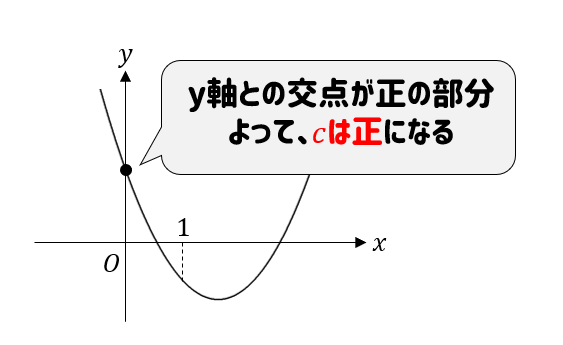
\(y\)軸との交点がプラスの部分になっているので、\(c>0\) であることが分かります。
答え
$$x>0$$
符号の決定(\(b^2-4ac\)の考え方)
| \(b^2-4ac\)の符号 | グラフの\(x\)軸との共有点の個数から判断する |
\(b^2-4ac\) っていう式は、どこかで見た覚えがあるよね。
そう、これは判別式だ!
なんだっけ…という方はこちらの記事で確認しておいてください。
>【二次関数の判別式】x軸との共有点、グラフの位置関係を考える問題を解説!
簡単にだけ説明しておくと
判別式である\(b^2-4ac\) の符号によって、共有点の個数を判断することができるというものでした。
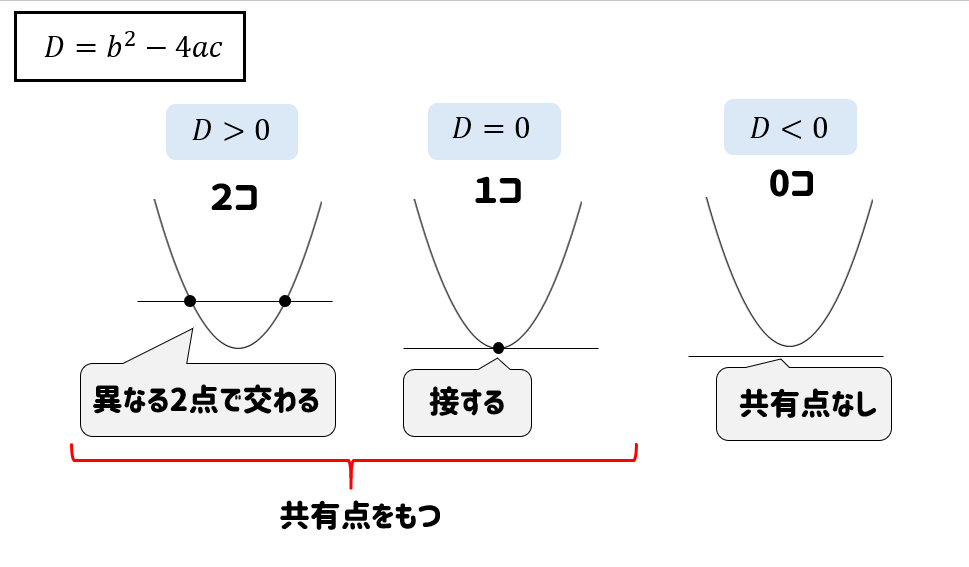
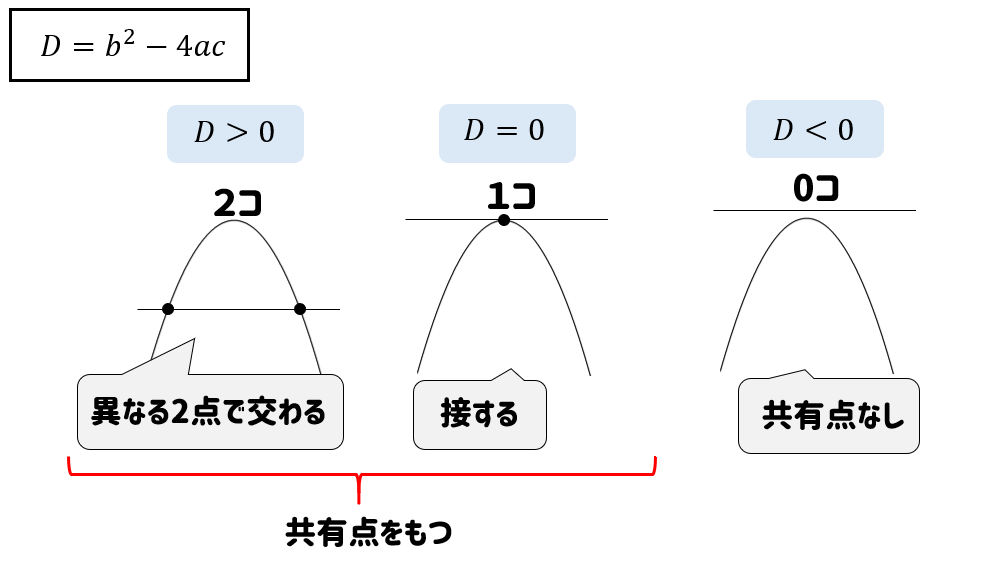
具体的には次のようになります。
つまり
共有点が2個なら\(b^2-4ac>0\)
共有点が1個なら\(b^2-4ac=0\)
共有点が0個なら\(b^2-4ac<0\) というわけです。
今回の問題では、判別式である\(b^2-4ac\) の符号を決定したいので、グラフから共有点の個数を読み取ります。
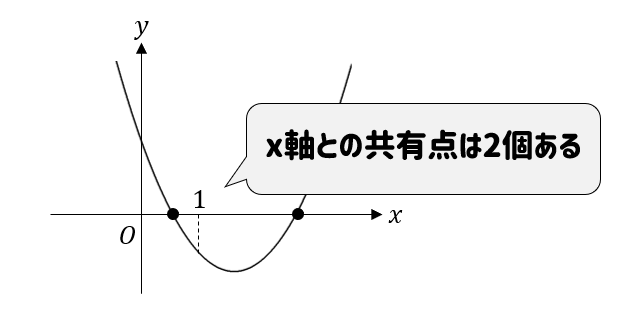
すると、共有点は2個であることが分かりますね。
よって、答えは\(b^2-4ac>0\) となります。
答え
$$b^2-4ac>0$$
符号の決定(\(a+b+c\)の考え方)
| \(a+b+c\)の符号 | \(x=1\) のときの\(y\)座標から判断する |
\(a+b+c\) とは、二次関数\(y=ax^2+bx+c\) において、\(x=1\) を代入したときにでてくる\(y\) の値です。
実際に\(x=1\) を代入すると、次のようになるよね。
$$\begin{eqnarray} y&=&a\times 1^2+b\times 1+c=a+b+c\end{eqnarray}$$
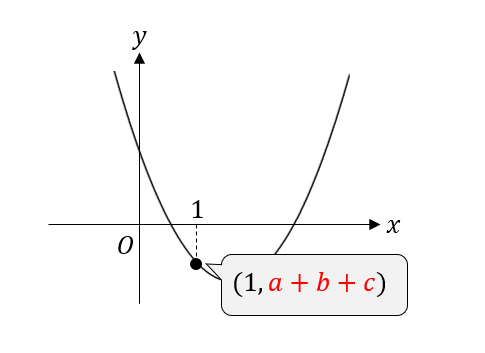
なので、今回の問題では
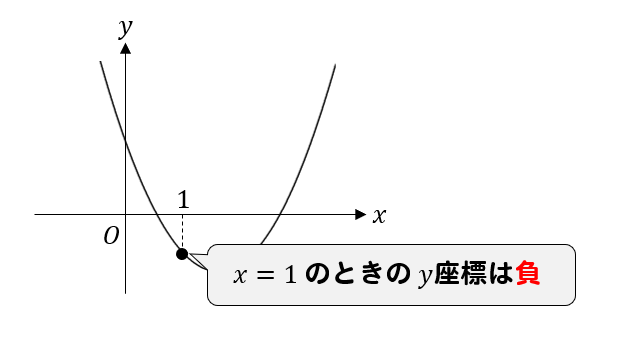
\(x=1\) のときの\(y\)座標は負であることが読み取れるので
答えは、\(a+b+c<0\) となります。
答え
$$a+b+c<0$$
符号の決定(\(a-b+c\)の考え方)
| \(a-b+c\)の符号 | \(x=-1\)のときの\(y\)座標から判断する |
\(a-b+c\) とは、二次関数\(y=ax^2+bx+c\) において、\(x=-1\) を代入したときにでてくる\(y\) の値です。
実際に\(x=-1\) を代入すると、次のようになるよね。
$$\begin{eqnarray} y&=&a\times (-1)^2+b\times (-1)+c=a-b+c\end{eqnarray}$$
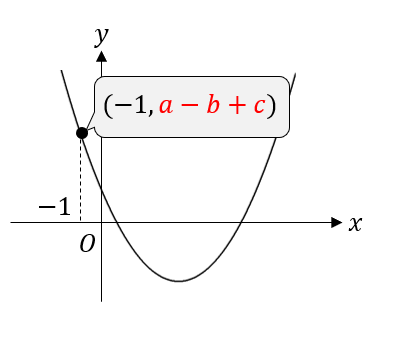
今回の問題では、\(x=-1\) の場所がハッキリとは分かりませんが
\(x<0\) となる部分では、常に\(y\)座標が正になっていることから、\(x=-1\)のときも正になると判断できますね。
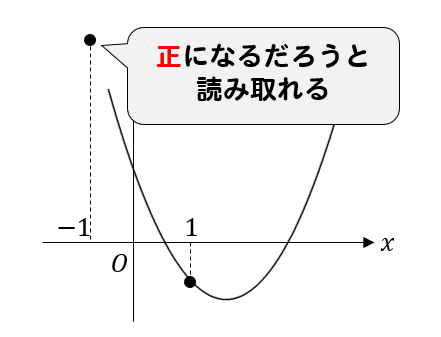
よって答えは、\(a-b+c>0\) となります。
答え
$$a-b+c>0$$
係数の符号決定【練習問題】
【問題】
二次関数\(y=ax^2+bx+c\) のグラフが下の図のようになっているとき、次の値の符号を求めなさい。
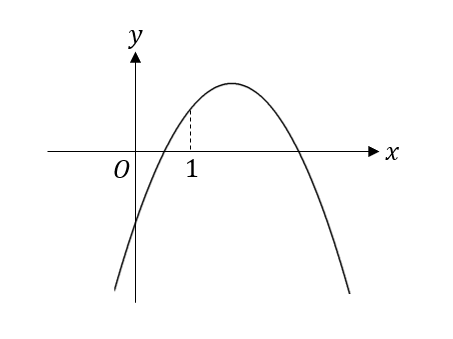
(1)\(a\) (2)\(b\) (3)\(c\) (4)\(b^2-4ac\) (5)\(a+b+c\) (6)\(a-b+c\)
まとめ!
お疲れ様でした!
それぞれの符号の決め方について理解できましたか?
やっぱり一番難しいのは、\(b\)の符号だね
ここはたくさん問題をこなして理解を深めておこう。
他の符号に関しては、見た目で判断するものばかりなので
テストでも得点源になるラッキー問題だね(^^)
- 一次関数の定義域、値域とは?問題の解き方を解説!
- 頂点の求め方、公式は?問題を使ってイチから解説!
- 平方完成!分数でくくるパターンの問題の解き方を解説!
- 平方完成!文字を含む式の場合は?やり方を丁寧に解説!
- 二次関数グラフの書き方を初めから解説!
- 二次関数の式の作り方をパターン別に解説!
- 二次関数を対称移動したときの式の求め方を解説!
- 平行移動したものが2点を通る式を作る方法とは?
- どのように平行移動したら重なる?例題を使って問題解説!
- 二次関数の最大・最小の求め方をイチから解説していきます!
- 場合分け!最大最小の応用問題の解き方をイチから解説!
- 2変数関数の最大・最小の求め方、パターン別の解説!
- 二次関数の文章題!高校で学習する問題をパターン別まとめ!
- 分数、小数、ルートを含む二次方程式の解き方まとめ!
- 高校数学で学習する連立方程式の解き方まとめ!
- 文字係数の方程式の解き方まとめ!
- 判別式Dを使って解の個数を調べてみよう!
- 2次方程式の共通解、kの値の求め方はどうやる??
- x軸との共有点、グラフの位置関係を考える問題を解説!
- 係数の符号の決定、グラフから符号を決めるポイントを解説! ←今回の記事
- x軸から切り取る線分の長さの求め方と公式!
- 放物線と直線の交点の求め方!
- 二次不等式の解き方を簡単に!高校数学をマスターしよう!
- 文字係数の2次不等式の解き方!場合分けの考え方は??
- 解からの係数決定!グラフの形と座標に注目せよ!
- 絶対不等式!パターン別の例題を使って解き方を解説!
- 2次方程式の解の存在範囲!判・軸・端の条件を見極めるのが重要!
- 4次不等式の解き方を例題解説!
- f(x) > g(x)となる範囲「すべての」「ある」の違いを理解しておこう!
- 絶対値のついたグラフを書いてみよう!


















とてもわかりやすくてたすかりました(^▽^)/
お役に立てて良かったです^^
わかりやすかったです!