今回は、高校数学Ⅰで学習する二次関数の式の作り方について、パターン別に解説していきます!
二次関数の式は、問題に与えられている情報によって式の形を使い分けていく必要があります。
この記事を通して、どの式を使えばよいのかを見極めれるようになりましょう!
今回取り上げる問題はこちら!
次の条件を満たす放物線をグラフにもつ二次関数を求めなさい。
(1)頂点が\((2,3)\)で、\((3,6)\)を通る。
(2)軸が\(x=-1\)で、2点\((0,5), (2,-3)\)を通る。
(3)3点\((-1,5), (2,5), (3,9)\)を通る。
(4)放物線\(y=2x^2\)を平行移動したもので、2点\((1,0), (-3,0)\)を通る。
(5)放物線\(y=x^2-3x+1\)を平行移動したもので、点\((2,3)\)を通り、その頂点は直線\(y=3x-1\)上にある。
(6)\(x=1\)のとき最小値\(2\)をとり、\(x=3\)のとき\(y=6\)となる。
二次関数の決定
二次関数の表し方は以下のようになります。
【一般形】
$$y=ax^2+bx+c$$
【標準形】
$$y=a(x-p)^2+q$$
【分解形】
$$y=a(x-α)(x-β)$$
問題で与えられている情報から、都合の良い式の形を使っていくようになります。
一般形
$$y=ax^2+bx+c$$
問題文で与えられた情報が、3点の座標のみのときにはこちらの式を活用していきます。

標準形
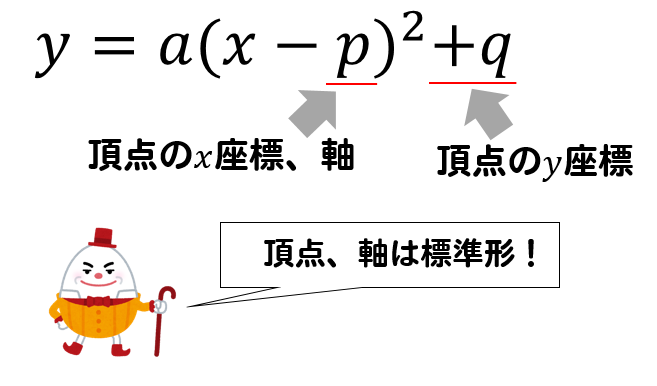
$$y=a(x-p)^2+q$$
問題文で与えられた情報に、頂点や軸といったものがある場合には、こちらの形を活用していきます。
分解形
$$y=a(x-α)(x-β)$$
こちらの分解形は、使う頻度は低めです。
だけど、覚えておくと便利なことも多いから是非覚えておこう!
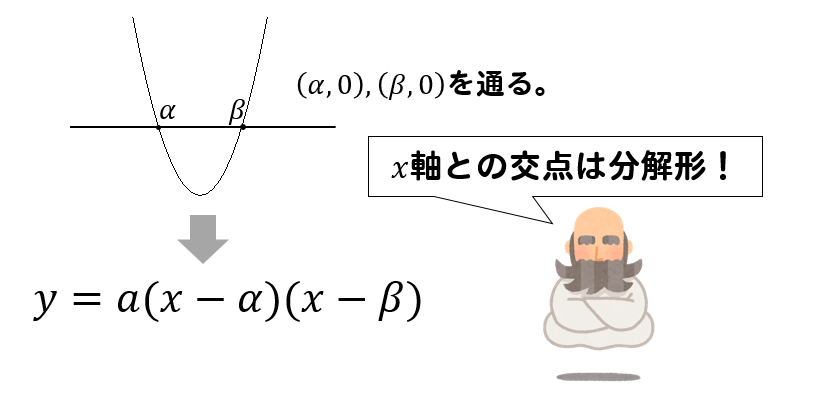
こちらの分解形は、\(x\)軸との交点の座標が与えられたときに活用します。
二次関数の決定、問題解説!
それでは、それぞれの問題の解き方について解説していきます。
(1)頂点パターン
問題文に頂点の情報が与えられているので
$$y=a(x-p)^2+q$$
標準形の形を活用していきます。
頂点\((2,3)\)を\(p, q\)にそれぞれ代入すると
$$y=a(x-2)^2+3$$
という形が作れます。
あとは、\(a\)の値が分かれば式が完成します。
ということで、次に
この二次関数は\((3,6)\)を通るから\(x=3, y=6\)を\(y=a(x-2)^2+3\)に代入してやります。
$$6=a(3-2)^2+3$$
$$6=a+3$$
$$a=3$$
よって、\(a\)の値が分かったので二次関数の式は
$$y=3(x-2)^2+3$$
となります。
頂点が与えられている問題では、標準形を活用して頂点の座標を代入。
次に\(a\)の値を求めるため、通る座標を代入。
こういう流れですね!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
(2)軸パターン
問題文に軸の情報が与えられているので
$$y=a(x-p)^2+q$$
標準形の形を活用していきます。
軸が\(x=-1\)ということなので、標準形の\(p\)部分に\(-1\)を代入。
$$y=a(x+1)^2+q$$
一旦、ここまで式を作ることができます。
更に、この式が2点\((0,5), (2,-3)\)を通るので
それぞれの値を式に代入して、式を2本作ります。
すると
$$5=a+q$$
$$-3=9a+q$$
このように\(a, q\)の2つの文字が残った2本の式が出来上がります。
あとは、これらを連立方程式で解いてやると
$$a=-1, q=6$$
となるので、二次関数の式は
$$y=-(x+1)^2+6$$
となります。
軸が与えられているときは、標準形を使い軸を代入。
次に通る2点の座標を代入し、連立方程式を解く。
という流れですね!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
(3)3点を通るパターン
問題文に与えられている情報が3点の座標のみだから
$$y=ax^2+bx+c$$
一般形の形を活用していきます。
3点の座標を一般形の式に代入して、3本の式を作ります。
すると
$$\begin{eqnarray} \left\{ \begin{array}{l}a-b+c=5 \\4a+2b+c=5 \\9a+3b+c=9\end{array} \right. \end{eqnarray}$$
このように3つの文字に関する連立方程式ができあがります。
あとは、この連立方程式を解くことで
$$a=1, b=-1, c=3$$
となるので、二次関数の式は
$$y=x^2-x+3$$
となります。
与えられた情報が3点の座標のみの場合、一般形の形を活用して連立方程式を解くことで二次関数の式を求めることができます。
んー、計算が多いから
正直…
この問題めんどいっすねw
まぁ、テストには出やすい問題だから面倒なんて言ってられないのですが(^^;
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
(4)x軸との交点パターン
問題文から\(x\)軸との交点が与えられているので
$$y=a(x-α)(x-β)$$
分解形の形を活用していきましょう。
さらに、押さえておきたいポイントがありますね。
『放物線\(y=2x^2\)を平行移動した』
とありますが、ここから今から求める二次関数の式は\(a=2\)であることが読み取れます。
平行移動した場合、\(x^2\)の係数は同じになるんでしたね!
以上より、分解形にそれぞれの情報を当てはめると
$$y=2(x-1)(x+3)$$
$$=2x^2+4x-6$$
となります。
この問題は、一般形を使っても解くことはできますが分解形を活用した方が圧倒的に楽です!
そのため、分解形の出番は少ないのですが覚えておいたほうがお得ですね(^^)
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
(5)頂点が直線上にあるパターン
ここからは、応用編になっていきます。
まず、問題分に頂点に関する情報が含まれているので
$$y=a(x-p)^2+q$$
標準形の形を活用していきます。
しかし、頂点の座標が具体的に分かっていないので、標準形の式に代入することができなくて困っちゃいますね(^^;
ということで、頂点の座標を自分で作ってしまいます!!
『頂点は直線\(y=3x-1\)上にある』
ということから、頂点の\(x\)座標を\(p\)とすると
頂点の\(y\)座標は、\(p\)を\(y=3x-1\)に代入して\(y=3p-1\)と表すことができます。
よって、頂点の座標を
$$(p, 3p-1)$$
と、自分で作ってやることができます。
更に
『放物線\(y=x^2-3x+1\)を平行移動』
ということから、\(a=1\)であることも読み取れます。
これらの情報を、標準形の形に代入すると
$$y=(x-p)^2+3p-1$$
と、式を作ることができます。
更に、この式は点\((2,3)\)を通るので
$$3=(2-p)^2+3p-1$$
という式が作れます。
あとは、この方程式を解くことで\(p\)の値を求めます。
$$3=4-4p+p^2+3p-1$$
$$p^2-p=0$$
$$p(p-1)=0$$
$$p=0, 1$$
よって、二次関数の式は
$$y=x^2-1$$
$$y=x^2-2x+3$$
となります。
頂点が直線上にあるという問題では、頂点を自分で作ってしまいましょう!!
(6)最大・最小値パターン
最小値が与えられたことから
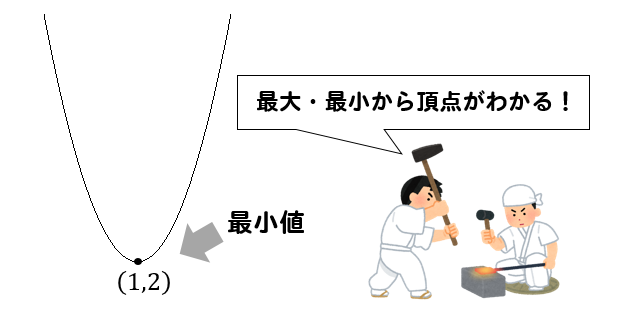
この二次関数は下に凸で、頂点は\((1,2)\)であることが読み取れます。
よって、頂点が分かるので
$$y=a(x-p)^2+q$$
標準形の形を活用していきます。
頂点は\((1,2)\)で、\(x=3\)のとき\(y=6\)となることから
$$y=a(x-1)^2+2$$
$$6=4a+2$$
$$4=4a$$
$$a=1$$
よって、二次関数の式は
$$y=(x-1)^2+2$$
$$=x^2-2x+3$$
となります。
二次関数の決定 まとめ
お疲れ様でした!
二次関数の式の決定では、問題文に与えられて情報からどの形の式を使うか判断する必要があります。
最後に確認して、終わりにしておきましょう。
3点の座標のみの場合
⇒ 【一般形】 \(y=ax^2+bx+c\)
頂点、軸が与えられた場合
⇒ 【標準形】 \(y=a(x-p)^2+q\)
\(x\)軸との交点が与えられた場合
⇒ 【分解形】\(y=a(x-p)^2+q\)
- 一次関数の定義域、値域とは?問題の解き方を解説!
- 頂点の求め方、公式は?問題を使ってイチから解説!
- 平方完成!分数でくくるパターンの問題の解き方を解説!
- 平方完成!文字を含む式の場合は?やり方を丁寧に解説!
- 二次関数グラフの書き方を初めから解説!
- 二次関数の式の作り方をパターン別に解説! ←今回の記事
- 二次関数を対称移動したときの式の求め方を解説!
- 平行移動したものが2点を通る式を作る方法とは?
- どのように平行移動したら重なる?例題を使って問題解説!
- 二次関数の最大・最小の求め方をイチから解説していきます!
- 場合分け!最大最小の応用問題の解き方をイチから解説!
- 2変数関数の最大・最小の求め方、パターン別の解説!
- 二次関数の文章題!高校で学習する問題をパターン別まとめ!
- 分数、小数、ルートを含む二次方程式の解き方まとめ!
- 高校数学で学習する連立方程式の解き方まとめ!
- 文字係数の方程式の解き方まとめ!
- 判別式Dを使って解の個数を調べてみよう!
- 2次方程式の共通解、kの値の求め方はどうやる??
- x軸との共有点、グラフの位置関係を考える問題を解説!
- 係数の符号の決定、グラフから符号を決めるポイントを解説!
- x軸から切り取る線分の長さの求め方と公式!
- 放物線と直線の交点の求め方!
- 二次不等式の解き方を簡単に!高校数学をマスターしよう!
- 文字係数の2次不等式の解き方!場合分けの考え方は??
- 解からの係数決定!グラフの形と座標に注目せよ!
- 絶対不等式!パターン別の例題を使って解き方を解説!
- 2次方程式の解の存在範囲!判・軸・端の条件を見極めるのが重要!
- 4次不等式の解き方を例題解説!
- f(x) > g(x)となる範囲「すべての」「ある」の違いを理解しておこう!
- 絶対値のついたグラフを書いてみよう!


















テスト前で大焦りだったので助かりました
どのサイトよりも分かりやすくて本当に全然分からなかったけどこのサイトに出会えて問題が解けるようになりました!感謝しかないです➿❤️テスト頑張ります‼️
ありがとうございます!!
テストがんばってください^^