【数学苦手な高校生向け】二次関数グラフの書き方を初めから解説！

今回は、高１で学習する二次関数の単元から

二次関数の放物線グラフの書き方を基礎から解説していくよ！

数学が苦手だ！

という方に向けて、丁寧に説明していくので

この記事を通して理解を深めていきましょう(^^)

動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします＾＾

高校メルマガ講座の無料登録はこちら！

Contents

二次関数の放物線グラフを書く手順
手順に沿ってグラフを書いてみよう！
まとめ

二次関数の放物線グラフを書く手順

それでは、早速

グラフを書く手順を紹介します。

グラフの手順

二次関数の式を見て、グラフの形を判断する
放物線の頂点を求める
$y$軸との交点を求める
2点を通るような放物線をかく

この１～４の手順を踏むことで二次関数のグラフを書くことができます！

それでは、手順を１つずつ詳しく見ていきましょう。

式を見て、グラフの形を判断する

二次関数のグラフは

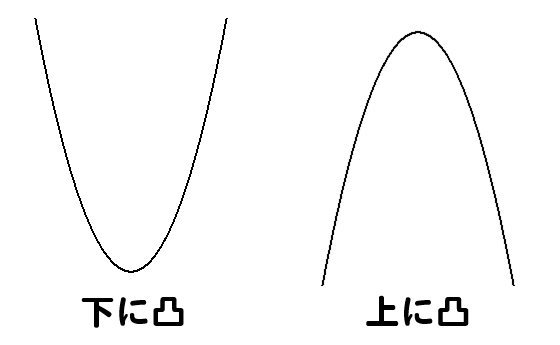
このように下に凸、上に凸の2種類あります。

では、二次関数の式を見たときに

どちらのグラフになるかを

どのように判断すればよいかと言うと

$x^2$の係数に注目しましょう！

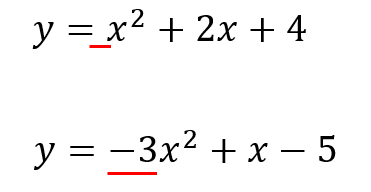
係数が＋であれば、下に凸の放物線。

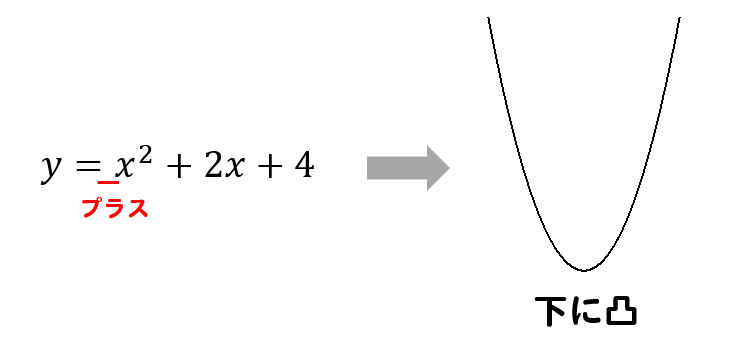
係数が－であれば、上に凸の放物線。

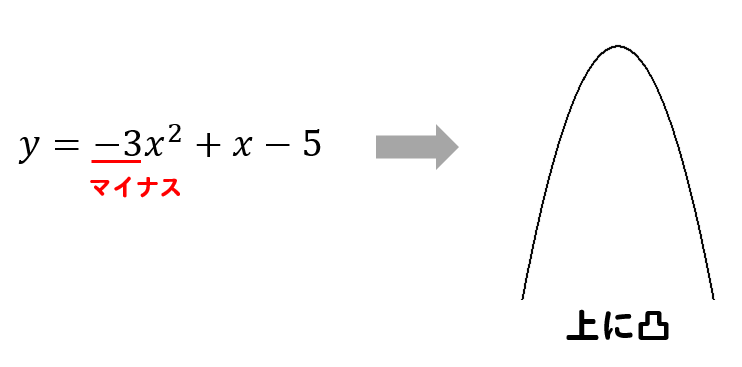
ということが判断できます。

グラフを書くためには、どちらの形になるのか知っておく必要があります。

まず、$x^2$の係数に注目してグラフの形を判別しましょう！

ポイント$x^2$の係数が＋　⇒　下に凸の放物線

$x^2$の係数が－　⇒　上に凸の放物線

グラフの形を判断する練習を少しだけしておきましょうか。

次の二次関数が下に凸、上に凸のどちらになるか判別しなさい。

（1）$y=x^2+4x+1$

解説＆答えはこちら

$x^2$の係数は1なので＋ですね。

よって、下に凸の放物線になります。

（2）$y=-3x^2+3x-9$

解説＆答えはこちら

$x^2$の係数は－3なので－ですね。

よって、上に凸の放物線になります。

（3）$y=3(x-1)^2+3$

解説＆答えはこちら

ちょっと見た目が違う式ですね(^^;

二次関数では、こういった形で表示されている式を扱うことがあります。

このときには、かっこの前についている数を$x^2$の係数と考えてください。

よって、$x^2$の係数は3なので＋ですね。

よって、下に凸の放物線になります。

放物線の頂点を求める

次は、放物線の頂点を求めましょう。

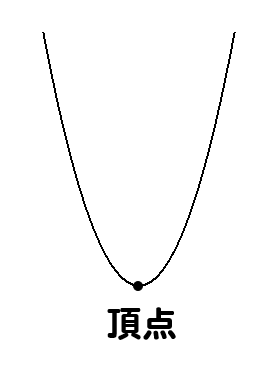
頂点というのは、このように放物線のてっぺん部分のことです。

この部分の場所が分からないと、正確なグラフを書くことができません。

それでは、どうやってグラフの頂点を求めれば良いのでしょうか。

頂点を求めるためには、平方完成と呼ばれる作業が必要になります。

例えば、$y=x^2+4x+3$の頂点を求める場合

$$\large{y=x^2+4x+3}$$

$$\large{=(x+2)^2-4+3}$$

$$\large{=(x+2)^2-1}$$

このように平方完成をしてやると

頂点の場所を求めることができます。

頂点の場所は、$(-2,-1)$ということがわかりますね！

平方完成の手順を忘れてしまった方はこちらをご参考ください＾＾

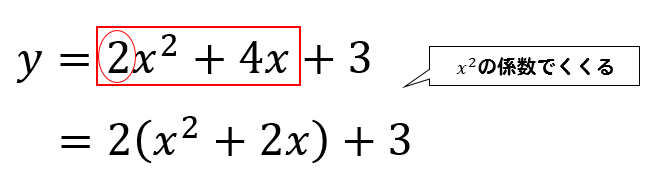
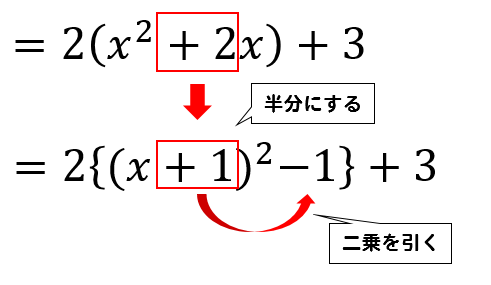
頂点を求める練習もしておきましょう！

次の二次関数の頂点を求めなさい。

（1）$y=(x+4)^2+1$

解説＆答えはこちら

最初から平方完成されている式であればラッキーですね(^^)

頂点は$(-4,1)$ということがすぐに読み取れたはず！

（2）$y=2x^2+4x-5$

解説＆答えはこちら

平方完成をして、頂点が分かる形に変形してやりましょう。

$$y=2x^2+4x-5$$

$$=2(x^2+2x)-5$$

$$=2\{(x+1)^2-1\}-5$$

$$=2(x+1)^2-2-5$$

$$=2(x+1)^2-7$$

よって、頂点は$(-1,-7)$ということが分かりますね！

二次関数の式に分数がでてきて、平方完成に困っている方はこちらの記事を参考にしてください(^^)

【平方完成】分数でくくるパターンの問題の解き方を解説！

$y$軸との交点を求める

頂点の場所が読み取れたら、次は$y$軸との交点を求めましょう。

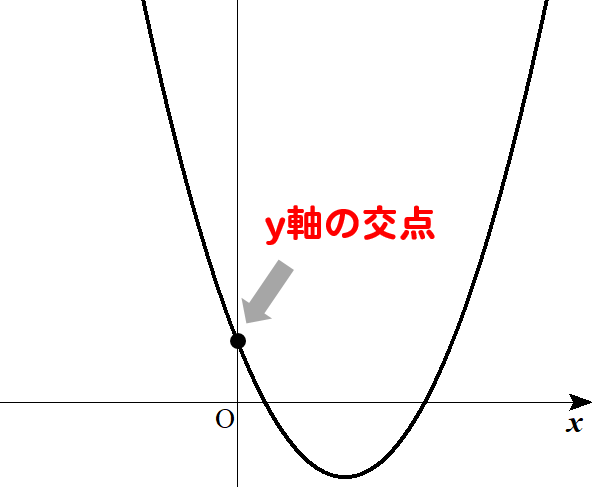
$y$切片とも呼ばれる場所です。

$y$軸と交わる場所は、$x=0$となる場所でもあります。

つまり、二次関数の式に$x=0$を代入すると$y$軸との交点を求めることができます。

$y=x^2+3x+4$のグラフであれば

$x=0$を代入して

$$y=0+0+4=4$$

よって、$(0,4)$の部分で交わることが分かります。

まぁ、何度も計算していると気づくとは思いますが

この部分を読み取れば、すぐに交点が分かりますね(^^)

ただし、平方完成された状態の式を扱う場合には

パッと見では交点が読み取れないので、$x=0$を代入して求めてやりましょう。

$$y=(x-3)^2+1$$

$x=0$を代入すると

$$y=(0-3)^2+1$$

$$=9+1$$

$$=10$$

よって、$(0,10)$で交わることがわかります。

2点を結ぶ放物線を書く

さぁ、最後の仕上げです。

放物線の形が分かっていて

頂点と$y$軸との交点も求まったので

その2点を結ぶ放物線を書いてやりましょう。

例えば、$y=x^2-2x+3$のグラフの場合

下に凸の放物線であり

頂点が$(1,2)$で、$y$軸との交点が$(0,3)$ということがわかるので

まずは、2点をとり

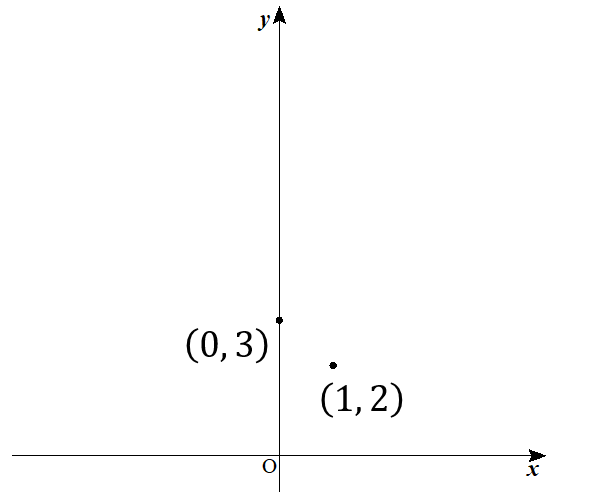
頂点をてっぺんとするような放物線を書いてやれば完成です！

ちゃんと左右対称に見えるように丁寧に線を引こうね(^^)

手順に沿ってグラフを書いてみよう！

次の二次関数のグラフを書きなさい。

$$y=-x^2+6x+5$$

まずは、グラフの形を判断します。

$x^2$の係数は－1なので、上に凸のグラフになることが分かります。

次に、式を平方完成して頂点を求めましょう。

$$\large{y=-x^2+6x+5}$$

$$\large{=-(x^2-6x)+5}$$

$$\large{=-\{(x-3)^2-9\}+5}$$

$$\large{=-(x-3)^2+9+5}$$

$$\large{=-(x-3)^2+14}$$

よって、頂点は$(3,14)$ということが分かります。

次は、$y$軸との交点を求めます。

これは式の定数項（文字がついていないやつ）を見ればすぐに分かるのでしたね！

ということで、$(0,5)$で交わることが分かります。

頂点と$y$軸との交点をそれぞれグラフに書いて

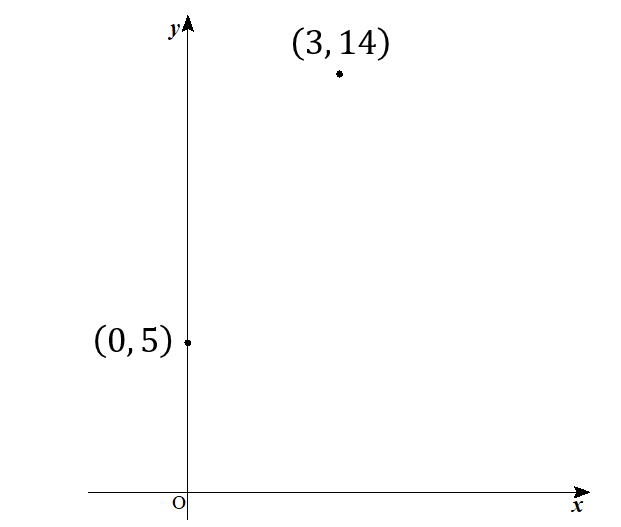
その2点を結ぶように上に凸の放物線を書いてやれば完成です！

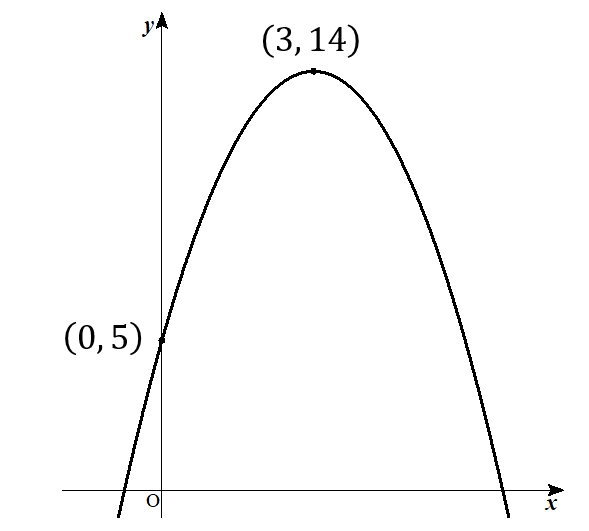
まとめ

お疲れ様でした！

二次関数のグラフの書き方についてまとめていきました。

手順の中でも紹介しましたが

グラフを書くためには、平方完成という式変形を正確にできるようにしておかないといけません。

平方完成に不安がある方は、まずは計算練習あるのみです！

グラフがちゃんと書けるようになると

二次関数の他の問題でも理解度が深まるはずです。

しっかりとマスターしていきましょう。

ファイトだー(/・ω・)/

こちらの記事も合わせてどうぞ！

テスト前に読ませていただきました！！
すごく分かりやすくて、理解力がとても低い私でもしっかりと理解することができました。
ありがとうございました。

【数学苦手な高校生向け】二次関数グラフの書き方を初めから解説！