今回の記事では、中学1年で学習する
「正負の数とは」
について解説していくよ！
中1で最初に学習する内容になるので、
しっかりと理解して、中学のスタートダッシュが切れるように頑張っていこう(/・ω・)/
正負の数とは
0より大きい数を正の数（せいのすう）
0より小さい数を負の数（ふのすう）といいます。
正の数を表すときには、＋（プラス）を使って
のように表します。
ただし、＋の符号は小学生のときと同じように省略して表すことの方が多いです。
一方で、負の数を表すときには、－（マイナス）の符号を使って
のように表します。
マイナスの符号は省略することができませんので、気を付けてくださいね！
省略しちゃったら、正の数と区別できなくなるもんね(^^;)
そして、絶対に覚えておいて欲しいのがコレ！
0は正でも負でもない数。
ということです。
0というのは、正と負の境界線となっている数です。
どちらにも属することのない特別な数だと覚えておきましょう。
そして、
正の整数のことを自然数（しぜんすう）といいます。
正の整数…？なんのこと？
って感じるかもしれませんが、単純なことです。
0より大きい数で、分数でも小数でもない数のこと。
それが自然数です。
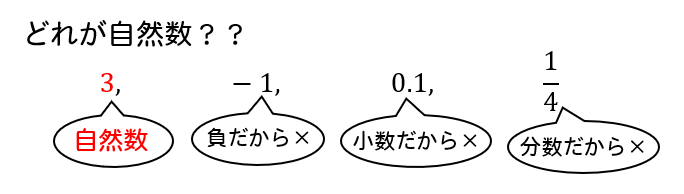
自然数は、順番を数えるときに使う数。
と覚えておくと便利です(^^)
順番を数えるときって、
\(1,2,3,4,5,\cdots \) で数えるよね。
この数が自然数っていうわけです。
まさか、順番を数えるときに負の数、小数、分数、0を使う人はいませんよね。
順番を数えるときに使わない数は、自然数ではない！
ってことで覚えておきましょう。
正負の数とは【練習問題】
【問題】
次の（ ）にあてはまる言葉をかきなさい。
- 0より大きい数を（①）といい、（②）の符号を使って表す。
- 0より小さい数を（③）といい、（④）の符号を使って表す。
- 正の整数のことを（⑤）という。
【問題】
次の数やことがらを、符号を使って表しなさい。
（1）\(0\)より\(5\)大きい数
（2）\(0\)℃より\(2.3\) ℃低い温度
【問題】
次の数について，下の問いに答えなさい。
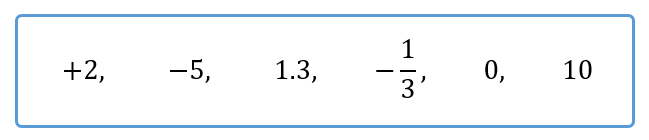
（1）整数をすべて答えなさい。
（2）正の数をすべて答えなさい。
（3）負の数をすべて答えなさい。
（4）自然数をすべて答えなさい。
（5）正でも負でもない数を答えなさい。
反対の性質の表し方
反対の性質をもつ量は、正の数と負の数を使って表すことができます。
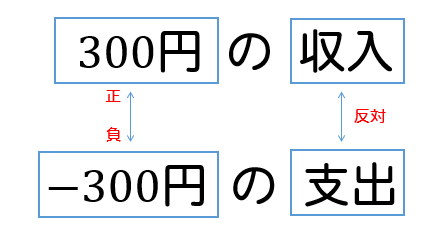
このように、正の数で表している量を負の数で表すためには反対の言葉を用います。
いくつか例題を見ながら確認しておきましょう。
【例題】
現在から\(30\)分後を \(+30\) 分と表すとき，現在から \(20\)分前は何と表せるか。
「後」を正の数を用いて表しているので、
その反対の言葉である「前」を表すときには負の数を用います。
よって、現在から\(20\)分前は \(-20\)分と表せます。
【例題】
地点Aから東へ\(5\)m進むことを \(+5\)mと表すとすると，\(-3\)mは何を表しているか。
東へ進むことを正の数で表しているので、
負の数は、その反対である「西へ進むこと」を表しています。
よって、\(-3\)mは「西へ\(3\)m進むこと」を表している。
【例題】
次のことを（ ）内の言葉を使って表しなさい。
\(300\)g重い（軽い）
反対の性質を表す言葉は、正負の数を入れかえて表します。
よって、\(-300\)g軽いと表せます。
【例題】
「\(-3000\)円の損失」を負の数を使わずに表しなさい。
符号が反対になるので、言葉も反対にして表す。
よって、\(3000\)円の利益と表せます。
以上のように、
反対の性質をもつ量は、正の数と負の数を使って表すことができます。
そして、この問題では、反対の性質を表す言葉を知っておく必要があります。
以下に反対の性質を表す言葉をまとめておくので覚えておいてくださいね！
北 ⇔ 南
東 ⇔ 西
後 ⇔ 前
高い ⇔ 低い
長い ⇔ 短い
重い ⇔ 軽い
収入 ⇔ 支出
利益 ⇔ 損失
正負の数とは【練習問題】
【問題】
次のことを符号を使って表しなさい。
（1）\(400\)円の収入を \(+400\)円と表すとき，\(1000\)円の支出
（2）ある地点から北に \(3\)m移動することを \(+3\)mと表すとき，南に \(5\)m移動すること
【問題】
ある時刻より \(10\)分後を \(+10\)分と表すとすると，\(-4\)分は何を表しているか。
【問題】
次のことを（ ）内の言葉を使って表しなさい。
（1）\(3\)℃上がる（下がる）
（2）\(7\)人多い（少ない）
（3）\(-4\)㎝高い（低い）
【問題】
「\(-900\)円の収入」を負の数を使わずに表しなさい。
まとめ！
正負の数の基礎については理解してもらえたかな？？
正負の数とは、で解説した数の分類についてはテストでもよく出題されています。
しっかりと理解してテストで高得点が取れるように頑張っていきましょう！
正負の基礎をクリアしたら
次は正負の大小、絶対値と進んでいきましょう！
がんばっているのに60点の壁をクリアできない中3生の方へ
頑張っているのに思うように成績が上がらず、
「このままだと本番で数学60点が厳しいかも…」
と不安に感じているあなた。
もしかして、
このような問題に直面していませんか？
- 模試になると点がガクッと落ちる
- 復習のやり方が分からない
- 勉強してもすぐに忘れる
- 凡ミスが直らない
- 家だと集中して勉強できない
- 問題集を買っても、1人で解けなくて途中でやめてしまう
- 友人が点を伸ばしていて焦る
- 頑張りたいから何をすればいいか教えて欲しい
僕が2年前に指導させてもらった中3のAくん
彼がまさにこのような状態でした。
すごく勉強したのに試験の結果が36点…
「どうすればいいか分からない…」
「点を上げれる自信がない…」
自信をなくし落ち込んでいましたが、
ある勉強方法を取り入れたことによって
Aくんは大変身！
なんと、たった2ヶ月で
36点 ⇒ 72点
なんと、驚きの36点UPを達成！
何をやっても点が伸びなかったAくん
彼を大変身させた「ある勉強方法」とは、
たったの3分で取り組める簡単なものです。
この勉強法を活用した人は、
43点 ⇒ 69点
67点 ⇒ 94点
人生初の100点！
このように次々と良い結果を報告してくれています＾＾
Aくんを大変身させた「ある勉強法」を
あなたにも活用してもらい
今すぐにでも結果を出して欲しいです。
そこで！
ある勉強法を正しく身につけてもらうための
1週間の集中メルマガ講座を作成しました。
こちらのメルマガ講座の中で、
順にワークをお渡ししていくので1つずつ取り組み、
やればやっただけ点が伸びていく感覚を掴んでくださいね！
もちろんこの講座の登録は無料！
いますぐワークを受け取っておきましょう('◇')ゞ
コメントを残す