【二次方程式】判別式Dを使って解の個数を調べてみよう！

二次方程式において、判別式っていうのを使うと

二次方程式の実数解の個数を調べることができます。

今回の記事では例題を通して

判別式の使い方を学んでいきましょう！

今回の内容はこちらの動画でも解説しています(‘◇’)ゞ

判別式の使い方

判別式\(D=b^2-4ac\)の符号を調べることで、二次方程式の実数解の個数を調べることができます。

え、判別式の公式って新しく覚えなきゃいけないんですか…とは思わないでくださいね。

判別式とは…

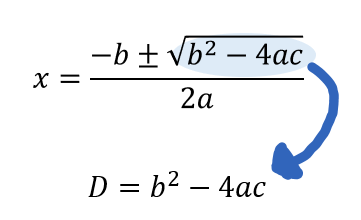
解の公式のルートの中身を取り出したものですね。

では、実際に判別式を使ってみましょう。

まずは、解の公式を使うときと同じように\(a,b,c\)の値を読み取りましょう。

そして、これらの値を判別式\(D=b^2-4ac\)に当てはめてみましょう。

$$\begin{eqnarray}D&=&(-5)^2-4\cdot 2\cdot 1\\[5pt]&=&25-8\\[5pt]&=&17>0 \end{eqnarray}$$

すると、判別式の値17は0より大きいことが分かります。

よって、判別式が\(D>0\)となるので

実数解の個数は2個

ということが分かりました。

判別式を使うと、わざわざ解を求めなくて個数を求めることができるので便利ですね(^^)

では、他の方程式においても判別式を使ってみましょう。

\(a=4, b=4,c=1\)が読み取れたら判別式に当てはめてみましょう。

$$\begin{eqnarray}D&=&4^2-4\cdot 4\cdot 1\\[5pt]&=&16-16\\[5pt]&=&0 \end{eqnarray}$$

よって、判別式の値が0になったので

実数解の個数は1個

ということが分かりました。

実数解が1個のときには重解といいます。

2個あった解が同じになって重なり、1個になったっていうイメージですね。

\(a=3, b=-6,c=5\)が読み取れたら判別式に当てはめてみましょう。

$$\begin{eqnarray}D&=&(-6)^2-4\cdot 3\cdot 5\\[5pt]&=&36-60\\[5pt]&=&-24<0 \end{eqnarray}$$

よって、判別式の値が負（\(D<0\)）になったので

実数解の個数は0個

となります。

ちなみに、数学Ⅱでは虚数というものを学習するようになります。

すると、\(D<0\)というのは

実数解はないけど、異なる2つの虚数解があるっていうことになります。

まぁ、これは別の記事にてお話しますね。

判別式の利用

判別式の問題は、個数を問われるだけではありません。

この章では判別式の利用問題について解説していきます。

実数解を持つというのは次のように考えることができます。

「実数解を持つ」＝「解が2個または1個になる」

ということから、\(D≧0\)になると考えられますね。

なので、二次方程式\(2x^2-3x+a=0\)が実数解をもつってことだから

判別式に当てはめたときに0以上になるってことがわかります。

$$\begin{eqnarray}D&=&(-3)^2-4\cdot 2\cdot a\\[5pt]&=&9-8a≧0\\[5pt]&&-8a≧-9\\[5pt]&&a≦\frac{9}{8}\cdots(解) \end{eqnarray}$$

このように、解の個数などが与えられ

そこから文字の範囲を求めさせるという問題がよく出題されます。

ここでは判別式の知識とは別に、不等式を解く知識も必要となります。

あわせてこちらの記事も復習しておきましょう。

⇒ 不等式の解き方まとめ！高校数学はこれでバッチリ！

⇒ 二次不等式の解き方を簡単に！高校数学をマスターしよう！

まとめ！

今回は二次方程式の判別式についてまとめておきました。

解の個数なんて調べて何になるんだ？

と疑問に思った方もいるかもしれません。

しかし、今回が学習した知識が二次関数の単元において、ものすごく重要になってきます。

だから今のうちにしっかりとマスターしておきましょうね！

ちなみに、二次関数での判別式はこちらの記事を！

⇒ 【二次関数の判別式】x軸との共有点、グラフの位置関係を考える問題を解説！