【苦手な人向け】二次関数を対称移動したときの式の求め方を解説！

今回は「二次関数の対称移動」について解説していきます。

ここの記事では、数学が苦手な人に向けてイチから学習していくぞ！

 

今回の内容は動画でも解説しています！

サクッと理解したい方はこちらをどうぞ(‘◇’)ゞ

対称移動とは

まず、対称移動とはどんなものなのか見ておきましょう。

\(x\)軸に関して対称移動とは次のようなものです。

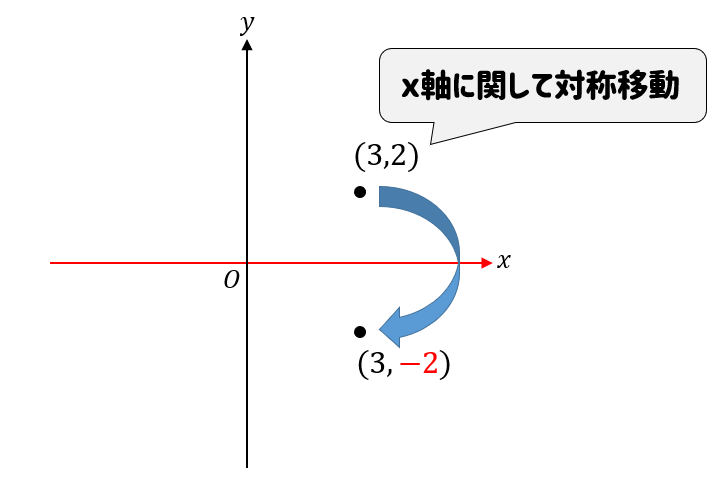
\(x\)軸を折れ目として、パタンと折り返した感じだね。

下に移動しているので、\(x\)座標はそのまま。\(y\)座標の符号がチェンジしていることが分かるね。

これを二次関数の放物線で考えても同じ。

このように\(x\)軸でパタンと折り返した形になります。

ここでポイントとして覚えておきたいのはコレ！

 

\(y\)軸に関して対称移動する場合には

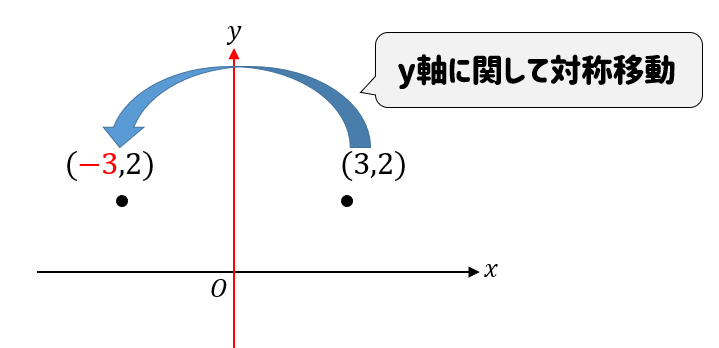
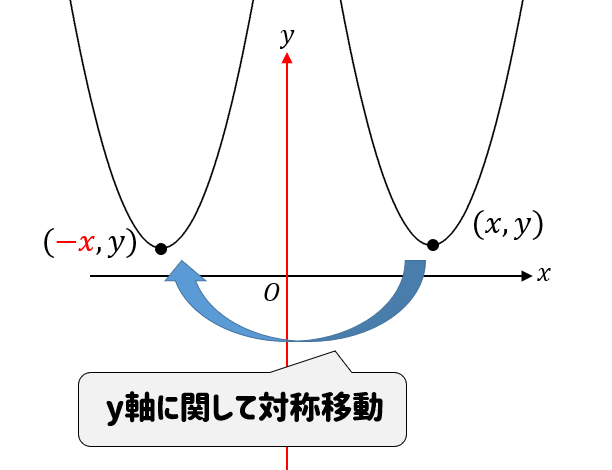
このように、\(y\)軸を折れ目としてパタンと折り返した形になります。

なので、\(x\)座標の符号がチェンジするということが分かりますね！

 

原点に関して対称移動する場合には

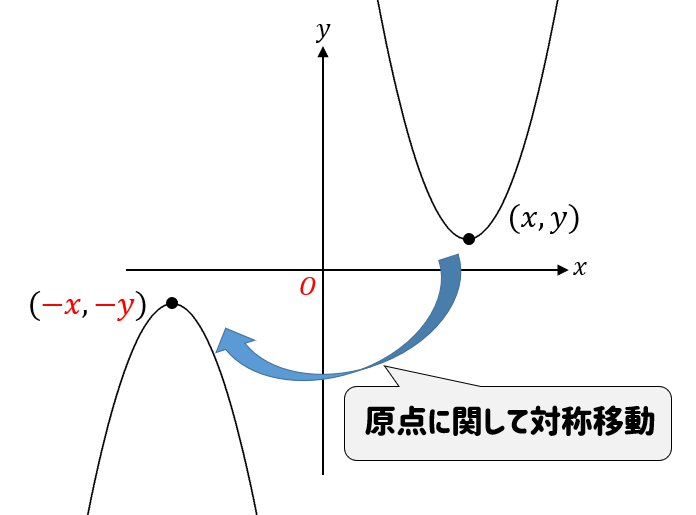
このように、斜めに移動したところになります。

つまり、\(x\)座標と\(y\)座標が両方とも符合チェンジすることが分かりますね！

 

対称移動をすると、どのような場所に移動するのか。

そして、座標はどのように変わるのか。

ご理解いただけましたか？？

これらのポイントをおさえた上で、次の章で問題を解いていきましょう！

二次関数を対称移動したときの式の求め方

それでは、以下のポイントをしっかりと押さえたうえで問題解説をしていきます。

 

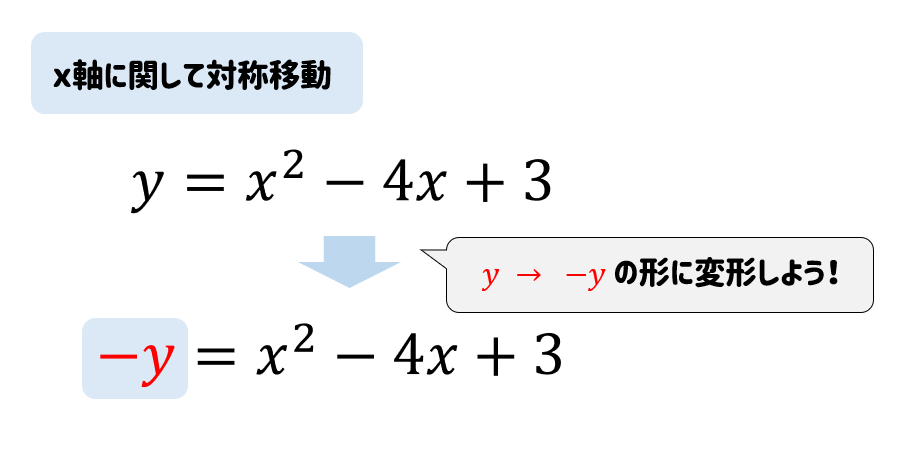
\(x\)軸に関して対称移動の式

\(x\)軸に関して対称移動する場合

$$\LARGE{y → -y}$$

これを覚えておけば簡単に解くことができます。

二次関数の式の\(y\)の部分を \(-y\) にチェンジしてしまえばOKです。

あとは、こちらの式を変形して\(y=\cdots\) にしていきましょう。

$$\begin{eqnarray}-y&=&x^2-4x+3\\[5pt]y&=&-x^2+4x-3 \end{eqnarray}$$

これで完成です！

簡単だね(^^)♪

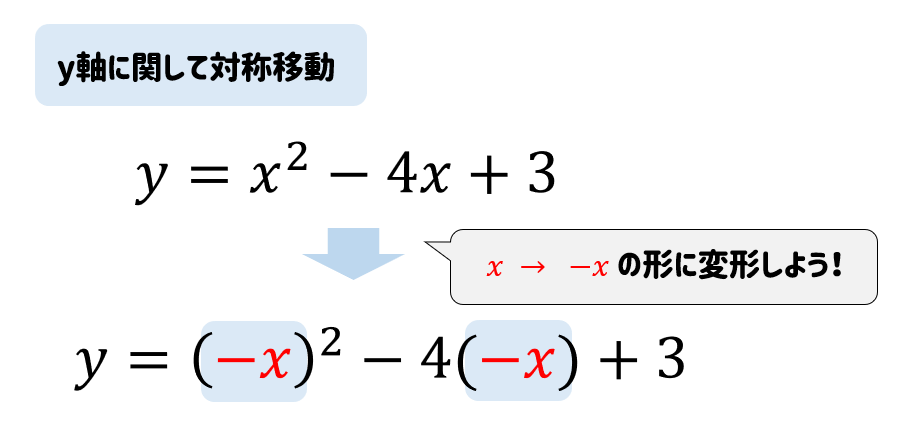
\(y\)軸に関して対称移動の式

\(y\)軸に関して対称移動する場合

$$\LARGE{x → -x}$$

これを覚えて

おけば簡単に解くことができます。

二次関数の式の\(x\)の部分を \(-x\) にチェンジしてしまえばOKです。

あとは、こちらの式を計算してまとめていきましょう。

$$\begin{eqnarray}y&=&(-x)^2-4(-x)+3\\[5pt]y&=&x^2+4x+3 \end{eqnarray}$$

これで完成です！

 

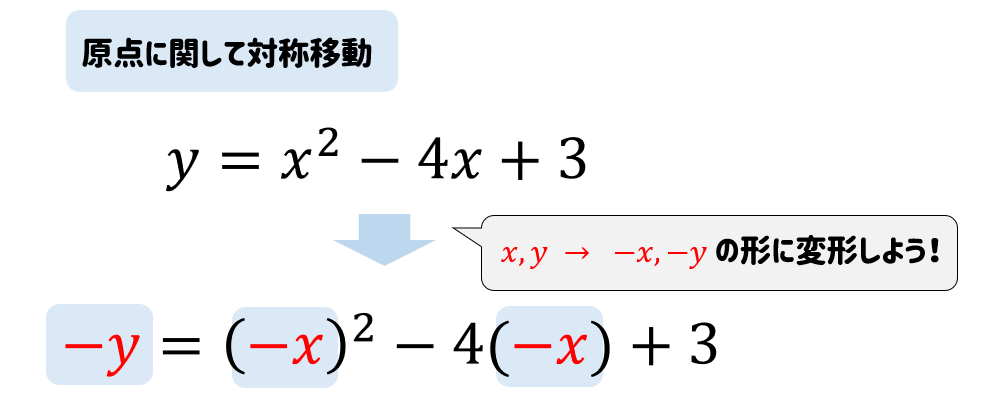
原点に関して対称移動の式

原点に関して対称移動する場合

$$\LARGE{x , y→ -x , -y}$$

これを覚えて

おけば簡単に解くことができます。

二次関数の式の\(x\)と\(y\)の部分を \(-x\)、\(-y\) にチェンジしてしまえばOKです。

あとは、こちらの式を変形して\(y=\cdots\) にしていきましょう。

$$\begin{eqnarray}-y&=&(-x)^2-4(-x)+3\\[5pt]-y&=&x^2+4x+3\\[5pt]y&=&-x^2-4x-3 \end{eqnarray}$$

これで完成です！

簡単、簡単(^^)♪

 

二次関数の対称移動【練習問題】

 

 

直線の式（y=1）に対する対称移動【応用】

では、次に二次関数の対称移動に関する応用問題にも挑戦してみましょう。

\(y=1\)に関して対称移動！？

って感じですが(^^;)

この場合は、落ち着いてグラフを書いて考えてみましょう。

\(y=x^2-2x+4\) の頂点を求めてグラフを書いてみると次のようになります。

 

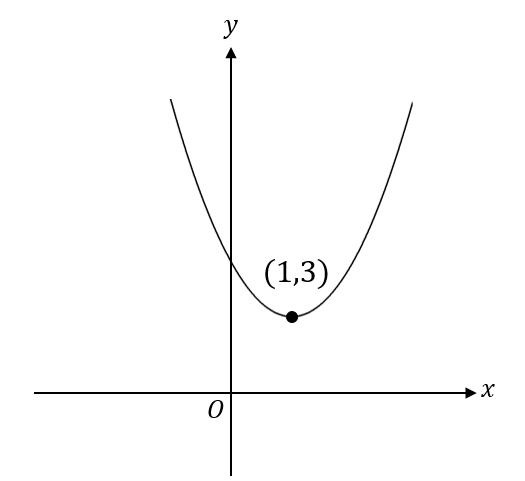
これを\(y=1\) で対称移動すると、次のような形になります。

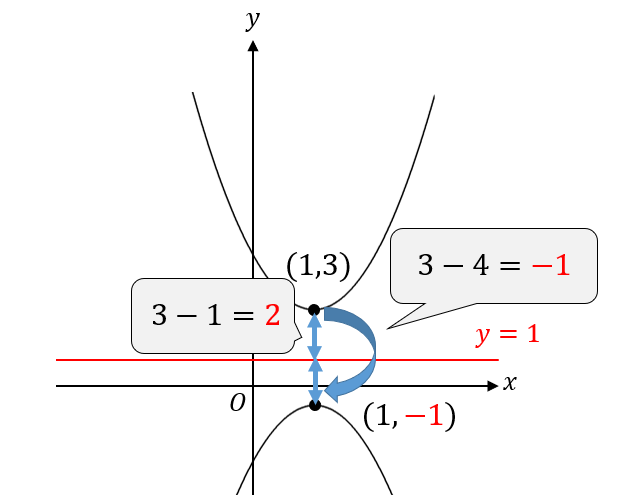
もとのグラフの頂点と\(y=1\) の距離は\(2\)です。

なので、対称移動されたグラフは\(y=1\) からさらに距離が\(2\)離れたところに頂点がくるはずです。

よって、対称移動されたグラフの頂点は\((1,-1)\)ということが分かります。

 

さらに大事なこととして！

対称移動された放物線の大きさ（開き具合）はもとのグラフと同じになるはずです。

だから、\(x^2\)の係数は同じ、または符号違いになります。

つまり数の部分は同じってことね！

 

今回のグラフは明らかにグラフの向きが変わっているので、\(x^2\)の係数が符号違いになるということがわかります。

このことから、\(y=1\)に関して対称移動されたグラフは\(x^2\)の係数が\(-1\)であり、頂点は\((1,-1)\)になるという情報が読み取れます。

よって、式を作ると次のようになります。

$$\begin{eqnarray}y&=&-(x-1)^2-1\\[5pt]&=&-x^2+2x-1-1\\[5pt]y&=&-x^2+2x-2 \end{eqnarray}$$

二次関数の対称移動【まとめ】

お疲れ様でした！

二次関数の対称移動は簡単でしたね(^^)

\(x,y\) のどちらの符号をチェンジすればよいのか。

この点を覚えておけば簡単に式を求めることができます。

 

あれ、どっちの符号をチェンジするんだっけ…？

と、なってしまった場合には自分で簡単なグラフを書いてみると思い出せるはずです。

\(x\)軸に関して対称移動とくれば、グラフを\(x\)軸を折れ目としてパタンと折り返してみましょう。

そのときに、座標は\(x\)と\(y\)のどちらが変化しているかな？

こうやって確認していけば、すぐに思い出すことができるはずです。

 

あとは、たくさん練習して知識を定着させていきましょう(/・ω・)/