【2次不等式】解からの係数決定！グラフの形と座標に注目せよ！

高校数学Ⅰで学習する2次不等式の単元から

「2次不等式の解からの係数決定」

について解説していきます。

 

取り上げる問題はこちら！

 

2次不等式の解から係数を求める問題では、

というのがポイントとなります。

 

不等式が0より大きいか、小さいか。

解の範囲が内側か、外側か。

ここに注目をしながら、グラフの形と2点の座標を見つけましょう。

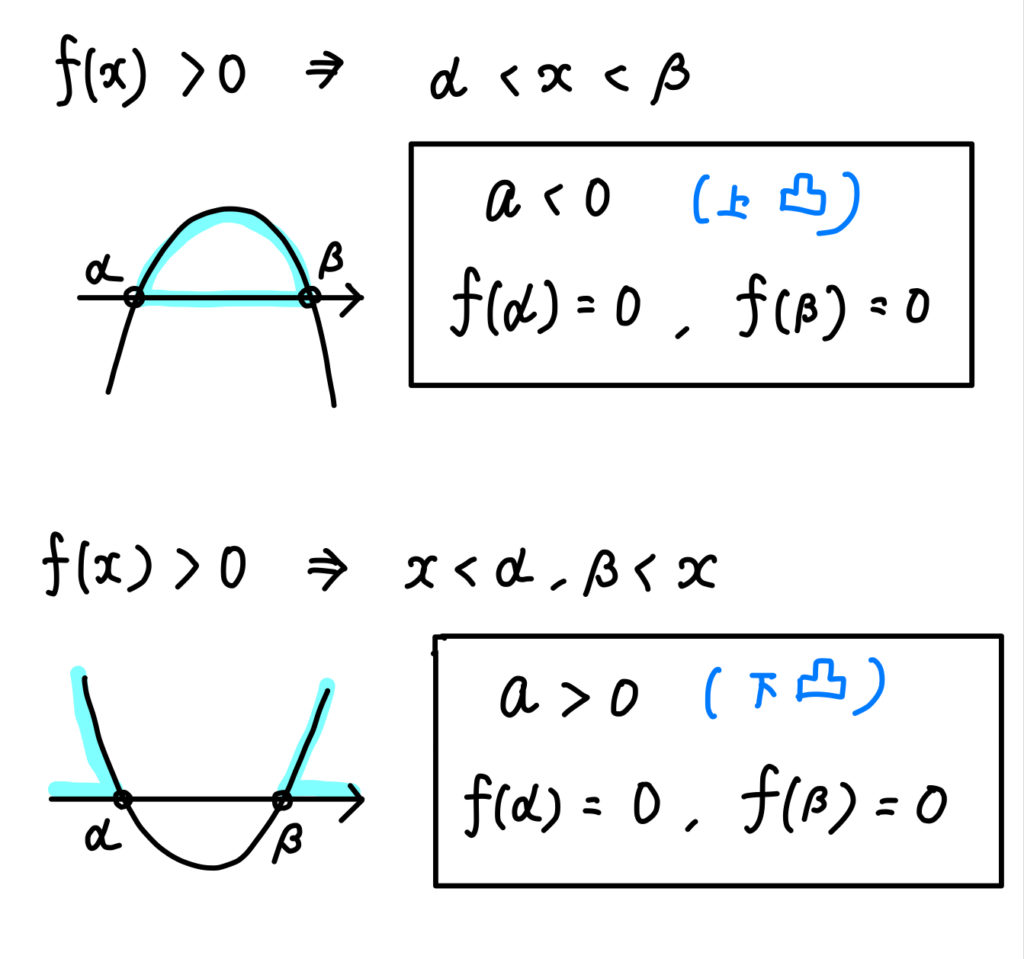
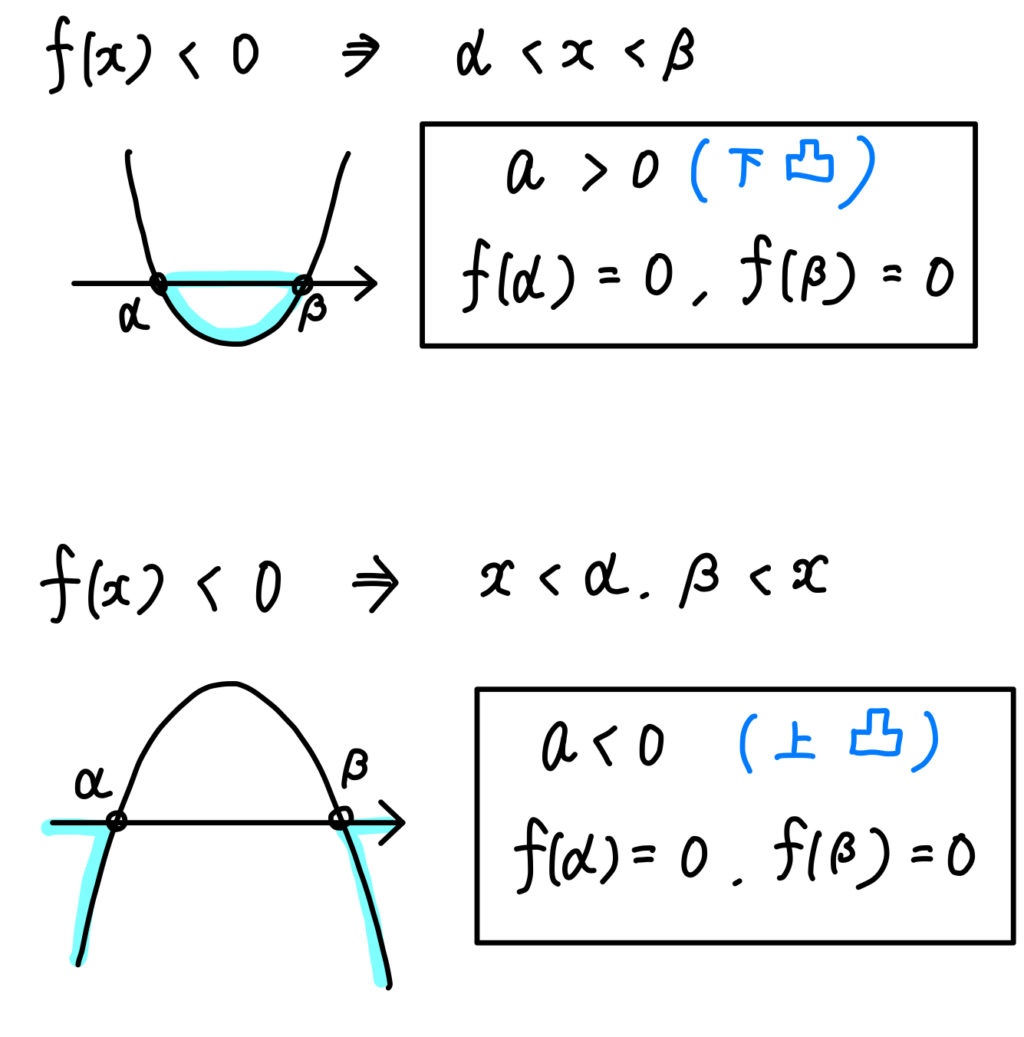
問題(1)の解説！

「\(\cdots<0\)」かつ「\(〇<x<△\)」の形なので、

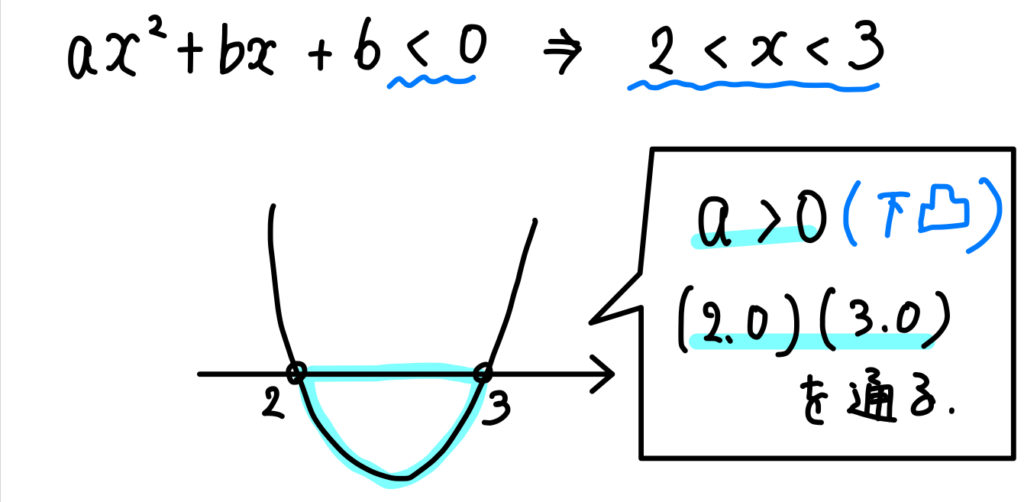
このように条件を読み取ることができます。

あとは計算を進めていきましょう。

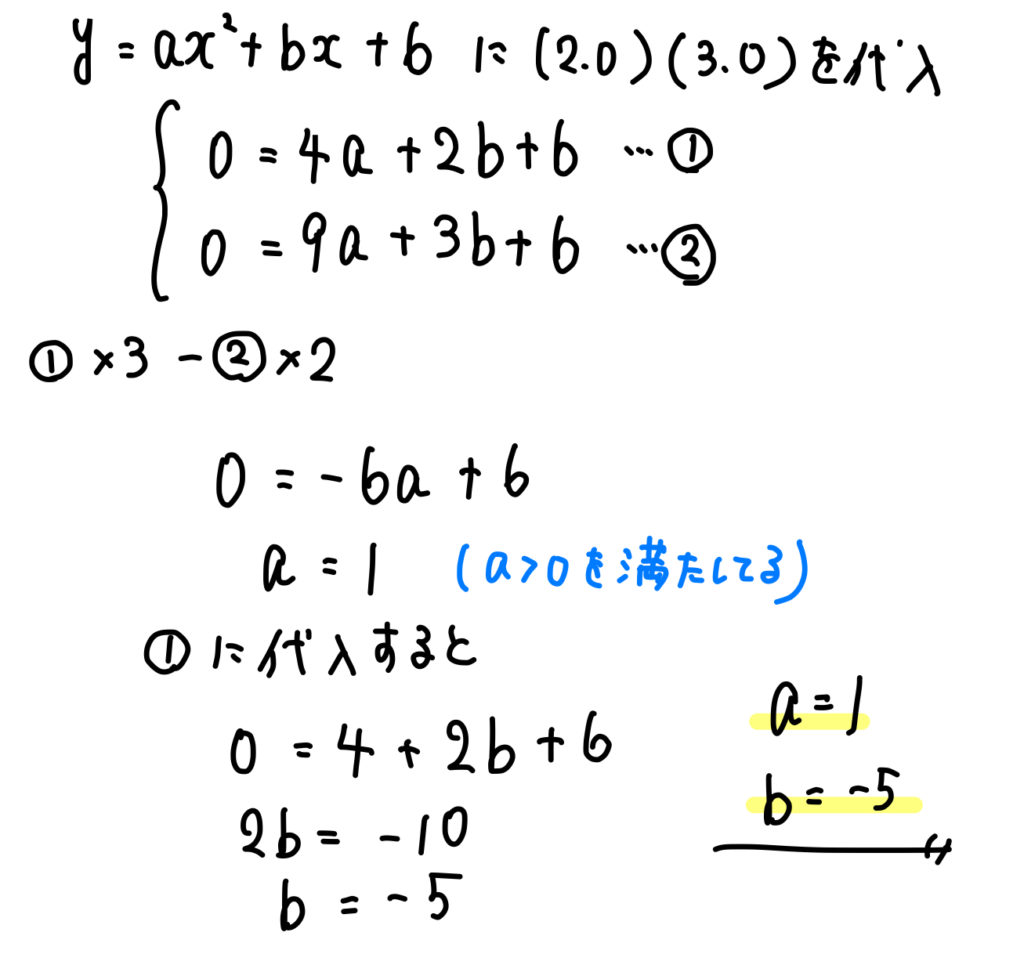
\(a\) の値を求めたとき、符号が条件を満たしているかどうかを確認するようにしてくださいね。

 

問題(2)の解説！

「\(\cdots<0\)」かつ「\(x<〇, △<x\)」の形なので、

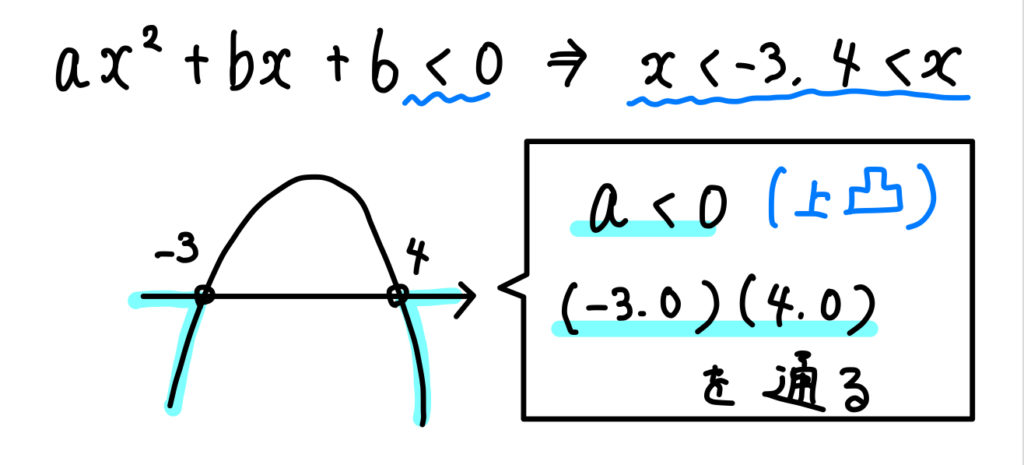
このように条件を読み取ることができます。

あとは計算を進めていきましょう。

 

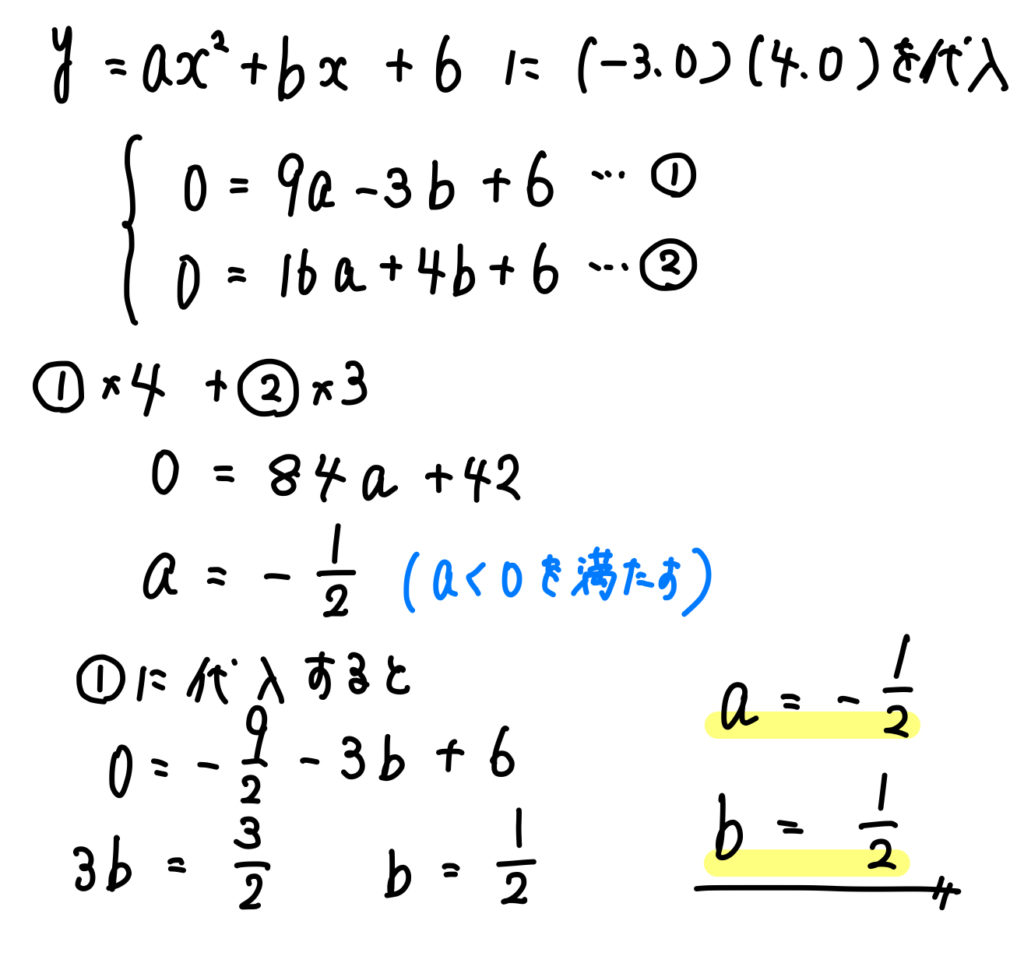
問題(3)の解説！

「\(\cdots>0\)」かつ「\(〇<x<△\)」の形なので、

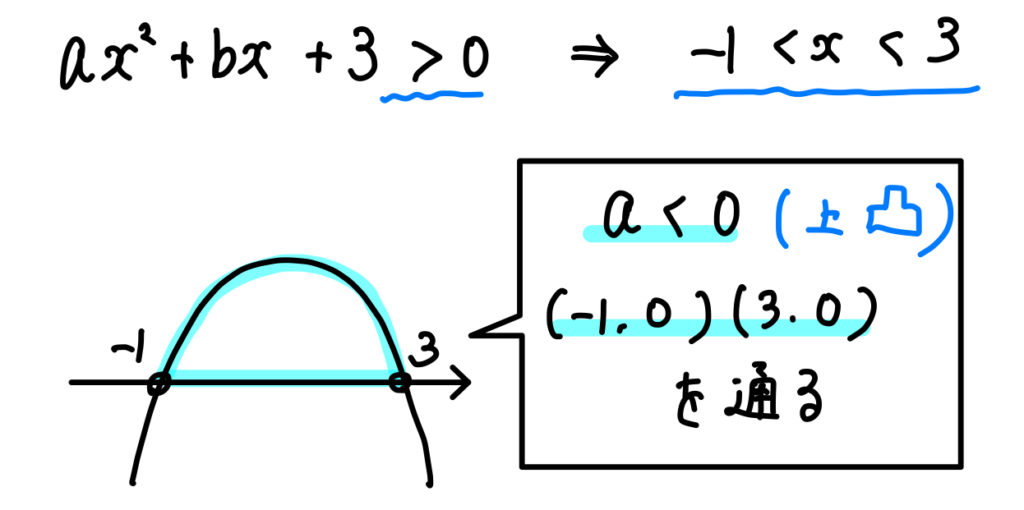
このように条件を読み取ることができます。

あとは計算を進めていきましょう。

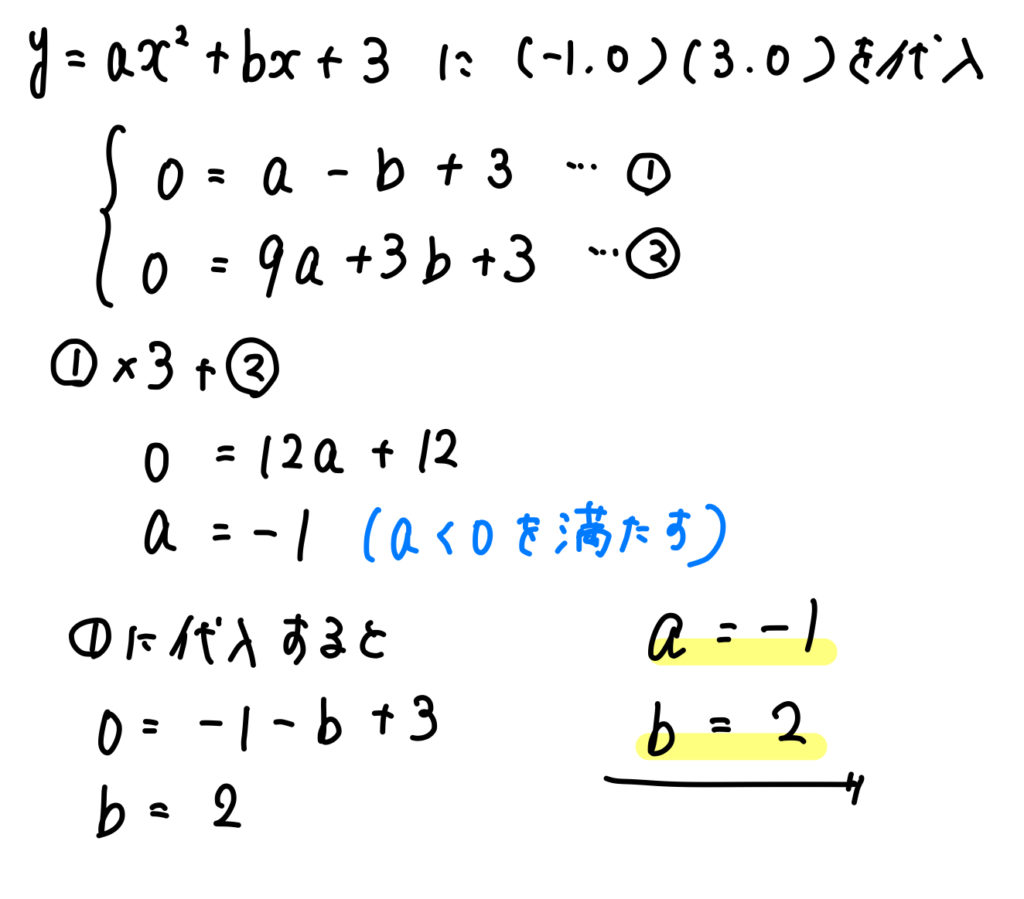
問題(4)の解説！

「\(\cdots≧0\)」かつ「\(x≦〇, △≦x\)」の形なので、

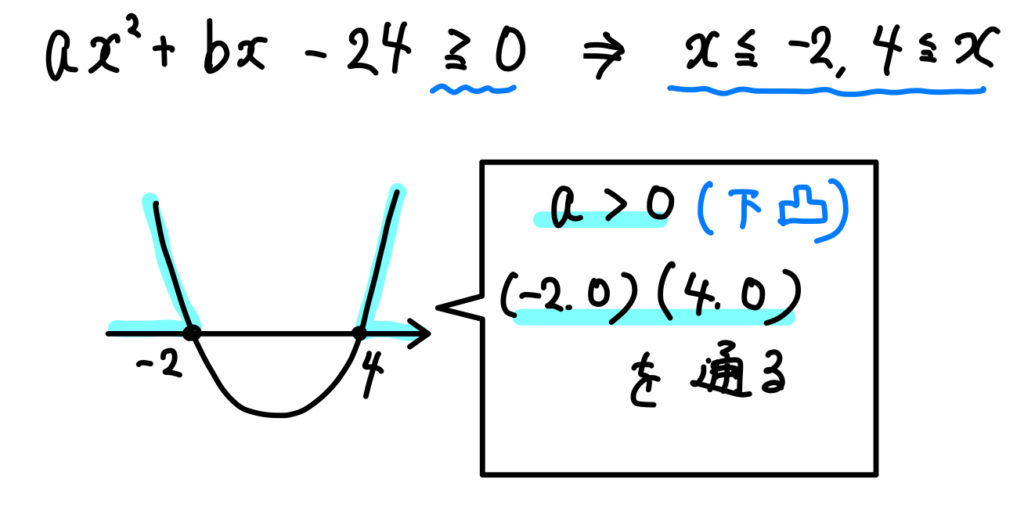
このように条件を読み取ることができます。

あとは計算を進めていきましょう。

 

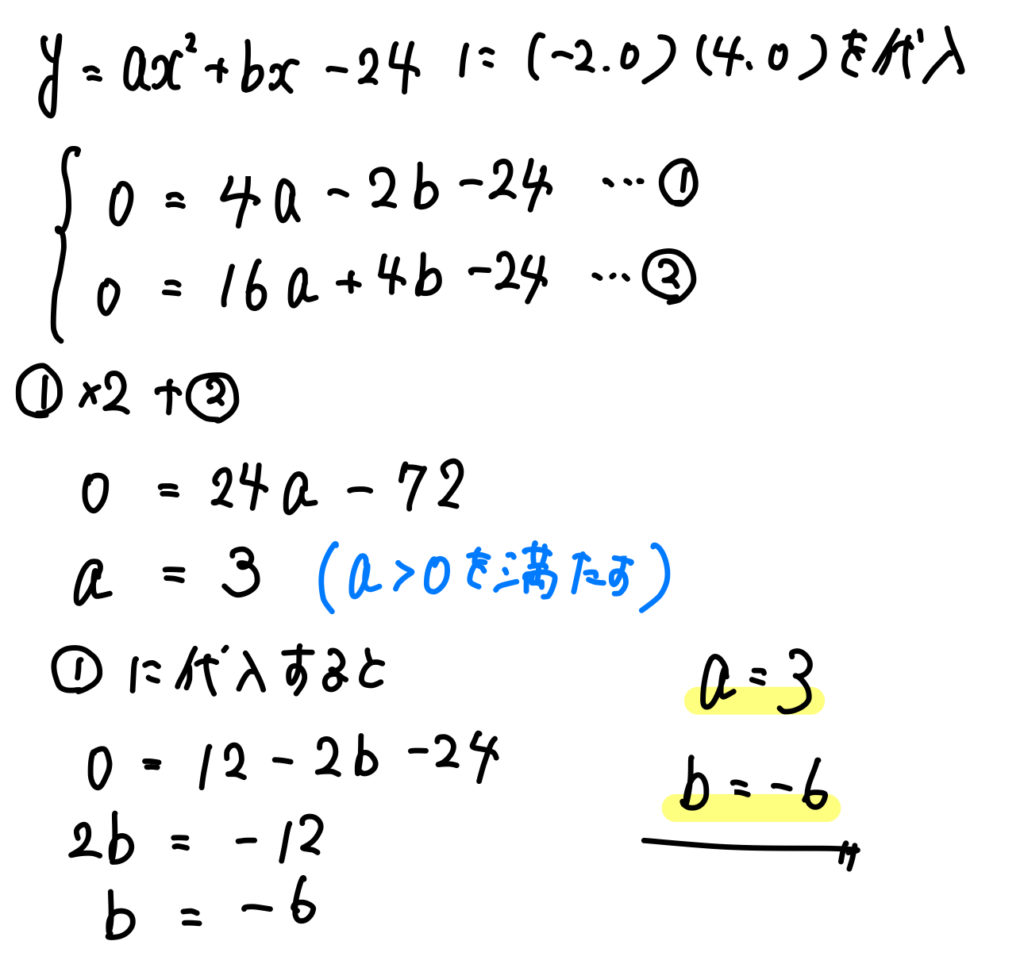
まとめ！

お疲れ様でした！

2次不等式の解法をグラフと絡めて理解できている人には、今回の問題は楽勝だったかと思います(^^)

グラフの形はどっちだろう…？と判断に困ってしまった方は、こちらの記事で2次不等式の基本を確認しておいてくださいね！