【二次関数の判別式】x軸との共有点、グラフの位置関係を考える問題を解説！

今回は二次関数の単元から「判別式」を使った問題を解説していきます。

結論から言ってしまうと

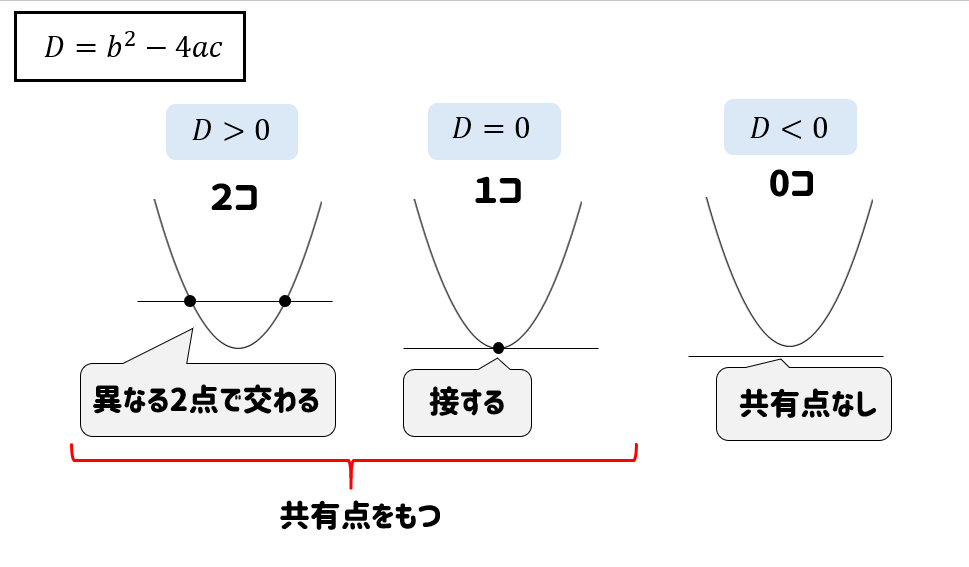
二次関数における判別式とはこんな感じだね！

では、問題においてどのように利用していくのか。

どのような問題が出題されるのか。

数学が苦手な人に向けてイチから解説していくぞ(/・ω・)/

 

今回の内容はこちらの動画でも解説しています！

二次関数の\(x\)軸との共有点の求め方と判別式！

まずは、二次関数の\(x\)軸との共有点を求める方法について考えてみよう。

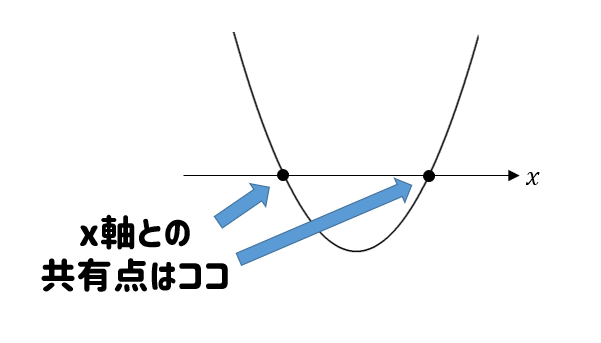
\(x\)軸との共有点っていうのは、ある特徴があるよね。

それは…

\(y\)座標が０にっている！！

ってことだ。

 

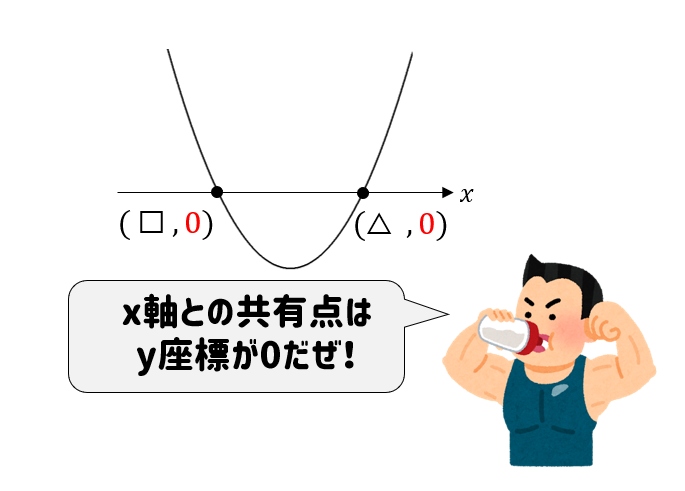
関数の座標を求めたい場合

\(x\)や\(y\)座標のどちらか一方がわかっているときには、関数の式に代入してやればOKだったよね。

っていうわけで、\(x\)軸との共有点の座標を求めるためには、

関数の式に\(y=0\) を代入すればよい！

ってことになります。

 

具体例を使って解説していきますね。

\(x\)軸との共有点を求めたいときには、\(y=0\) を代入する！でしたね。

$$\begin{eqnarray}0&=&x^2+2x-3\\[5pt]&=&(x+3)(x-1)\\[5pt]x&=&-3,  1\end{eqnarray}$$

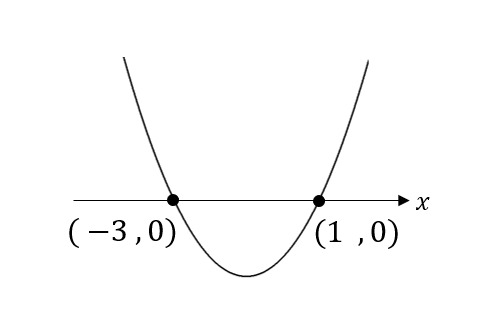
このように\(x\)軸との共有点は、\((-3,0)\)と\((1,0)\) であることが求まりました！

 

つまり！

このことから何が言いたいかというと…

ってことだね。

関数の問題ではあるんだけど、やっていることは二次方程式の解を求めているだけです。

ということは、二次方程式の個数がいくつあるのか分かればそれが、そのまま共有点の個数になるのではないか！

と、気が付くことができますね(^^)

 

そういうわけで

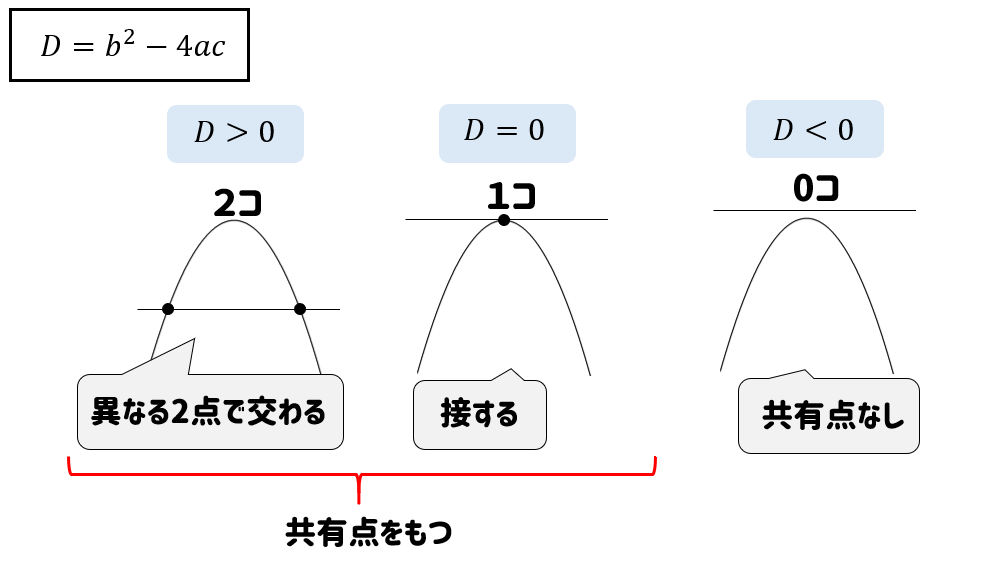
二次関数の判別式を調べると、上のような位置関係になっているわけです。

二次関数の判別式を使った問題の解き方！

それでは、判別式を使った問題を見ていきましょう。

共有点の個数を求める問題

それぞれ判別式にあてはめて共有点の個数を求めてみましょう。

まずは（1）から！

\(y=x^2-3x+2\)  という式から\(a=1,  b=-3,  c=2\)  となるので

$$\begin{eqnarray}D&=&(-3)^2-4\times 1\times 2\\[5pt]&=&9-8\\[5pt]&=&1>0 \end{eqnarray}$$

よって、判別式の値が正になるので共有点の個数は2個です。

 

次は（2）！

\(y=3x^2+x+1\)  という式から\(a=3,  b=1,  c=1\)  となるので

$$\begin{eqnarray}D&=&1^2-4\times 3\times 1\\[5pt]&=&1-12\\[5pt]&=&-11<0 \end{eqnarray}$$

よって、判別式の値が負になるので共有点の個数は0個です。

 

最後に（3）！

\(y=-x^2-4x-4\)  という式から\(a=-1,  b=-4,  c=-4\)  となるので

$$\begin{eqnarray}D&=&(-4)^2-4\times (-1)\times (-4)\\[5pt]&=&16-16\\[5pt]&=&0 \end{eqnarray}$$

よって、判別式の値が0になるので共有点の個数は1個です。

 

二次関数の式を判別式に当てはめて

正なら2個、0なら1個、負なら0個ですね。

単純な計算ができればOKな簡単な問題です(^^)

 

条件から文字の値を求める問題

このように、条件を与えられて文字の値を求めさせるという問題は頻出です。

ただ、全然難しくありません(^^)

二次関数\(y=x^2+mx+1\) のグラフが\(x\)軸に接する

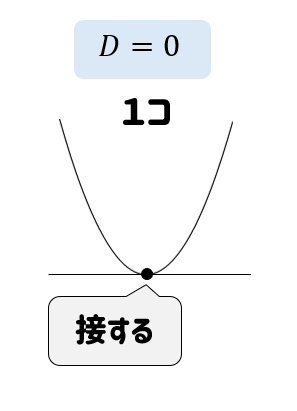
つまり、共有点が1個になるということですから

\(y=x^2+mx+1\) の判別式Dの値は0になるはずです。

\(a=1,  b=m,  c=1\) で判別式をとると

$$\begin{eqnarray}D&=&m^2-4\times 1\times 1\\[5pt]&=&m^2-4=0 \end{eqnarray}$$

あとは、この\(m\) の二次方程式を解いていけばよいです。

$$\begin{eqnarray}m^2-4&=&0 \\[5pt]m^2&=&4\\[5pt]m&=&\pm2\end{eqnarray}$$

 

共有点を持つというのがポイントです。

共有点を持つとだけ条件を指定された場合には

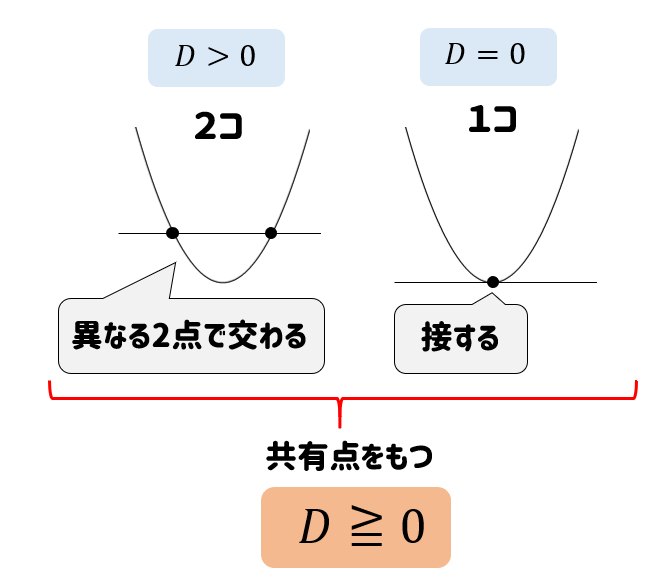
このように2個、1個のときが考えられます。

よって、\(y=x^2-4x+m\)の判別式Dは0以上になるということが読み取れます。

\(a=1,  b=-4,  c=m\) で判別式をとると

$$\begin{eqnarray}D&=&(-4)^2-4\times 1\times m\\[5pt]&=&16-4m≧0 \end{eqnarray}$$

あとは、この\(m\) の不等式を解いていけばよいです。

$$\begin{eqnarray}16-4m&≧&0 \\[5pt]-4m&≧&-16\\[5pt]m&≦&4\end{eqnarray}$$

逆に、共有点を持たない…という条件が与えられた場合には共有点が0個という意味ですから判別式Dは負になると考えればよいですね。

位置関係がどのように変わるかの問題

共有点の個数を問われているので、二次関数の式を判別式に当てはめてみましょう。

\(a=1,  b=-2,  c=k\) なので

$$\begin{eqnarray}D&=&(-2)^2-4\times 1\times k&=&4-4k \end{eqnarray}$$

よって、判別式の値は \(4-4k\) となったわけですが…

このままでは、判別式の符号が判断できず共有点の個数が分かりませんね。

なので、ここからパターンを分けて考えていきます。

判別式が正になれば、共有点が2個になるのだから

$$\begin{eqnarray}4-4k&>&0\\[5pt]4&>&4k\\[5pt]1&>&k \end{eqnarray}$$

 

判別式が0になれば、共有点が1個になるのだから

$$\begin{eqnarray}4-4k&=&0\\[5pt]4&=&4k\\[5pt]1&=&k \end{eqnarray}$$

 

判別式が負になれば、共有点が0個になるのだから

$$\begin{eqnarray}4-4k&<&0\\[5pt]4&<&4k\\[5pt]1&<&k \end{eqnarray}$$

最後に、これらをまとめると答えは次のようになります。

二次関数の判別式まとめ！

お疲れ様でした！

最後にもう1度、判別式についてまとめておきましょう。

 

判別式は、そこまで複雑な計算ではありませんし、

出題される問題もしっかりと意図をくみ取ることができれば簡単ですね(^^)

しっかりと確認しておきましょう！