今回は二次関数の単元から、放物線と直線の交点の座標を求める方法について解説していきます。
こんな問題だね!
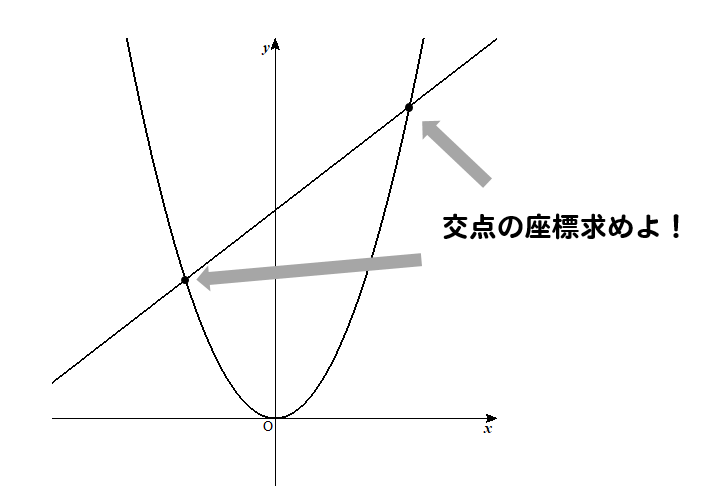
これは中3で学習する\(y=ax^2\)の単元でも出題されます。
中学生、高校生の両方の目線から問題解説をしていきますね(^^)
グラフの交点座標の求め方
グラフの交点を求めるためには
それぞれのグラフの式を連立方程式で解いて求めることができます。
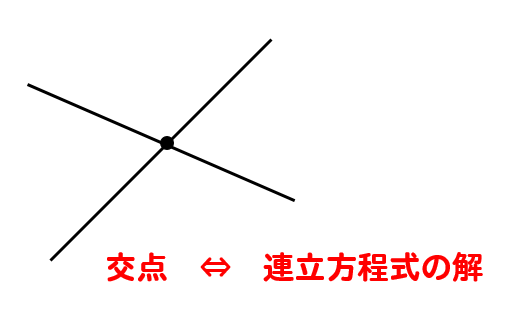
これは、直線と直線のときだけでなく
直線と放物線
放物線と放物線であっても
グラフの交点を求めたいときには連立方程式を解くことで求めることができます。
【中学生】放物線と直線の交点を求める問題
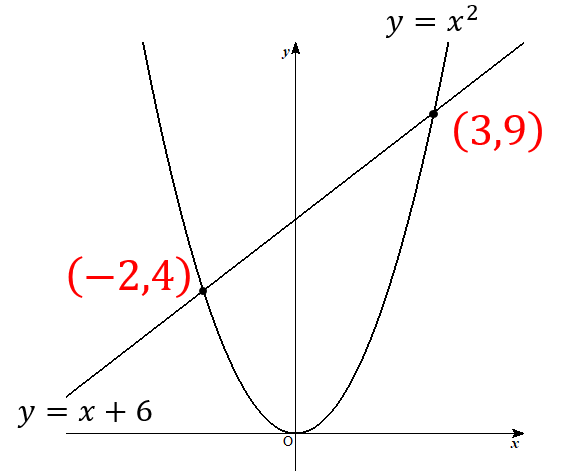
直線\(y=x+6\)と放物線\(y=x^2\)の交点の座標を求めなさい。
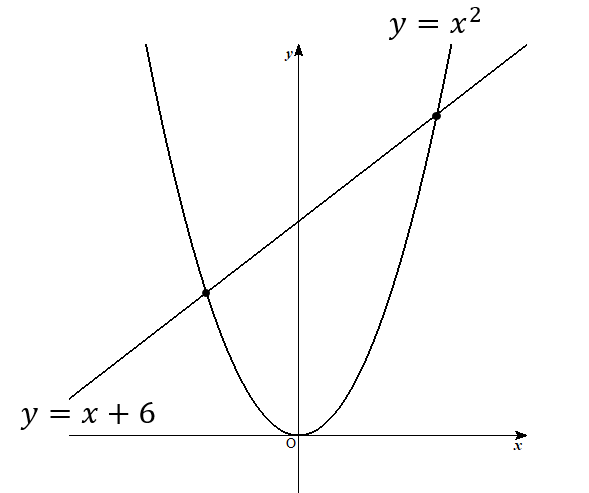
交点の座標を求めるためには、2つの式を連立方程式で解いてやればいいので
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}y=x+6 \\y=x^2 \end{array} \right. \end{eqnarray}}$$
こういった連立方程式を作ります。
代入法で解いてあげましょう!
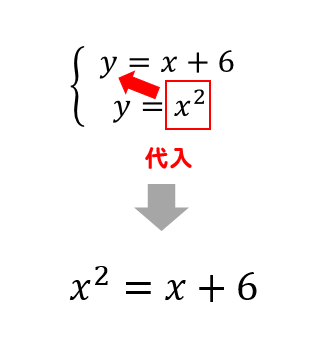
$$x^2=x+6$$
$$x^2-x-6=0$$
$$(x-3)(x+2)=0$$
$$x=3, -2$$
\(x=3\)を\(y=x+6\)に代入すると
$$y=3+6=9$$
\(x=-2\)を\(y=x+6\)に代入すると
$$y=-2+6=4$$
これにより、それぞれの交点が求まりました(^^)
【高校生】放物線と直線の交点を求める問題
直線\(y=-5x+4\)と放物線\(y=2x^2+4x-1\)の交点の座標を求めなさい。
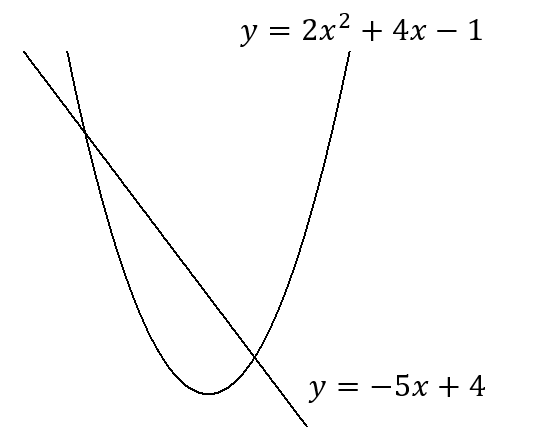
中学生で学習する放物線は、必ず原点を通るものでした。
一方、高校生での二次関数は少し複雑なものになります。
だけど、解き方の手順は同じです。
それでは、順に見ていきましょう。
まずは連立方程式を作ります。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}y=-5x+4 \\y=2x^2+4x-1 \end{array} \right. \end{eqnarray}}$$
代入法で解いていきましょう。
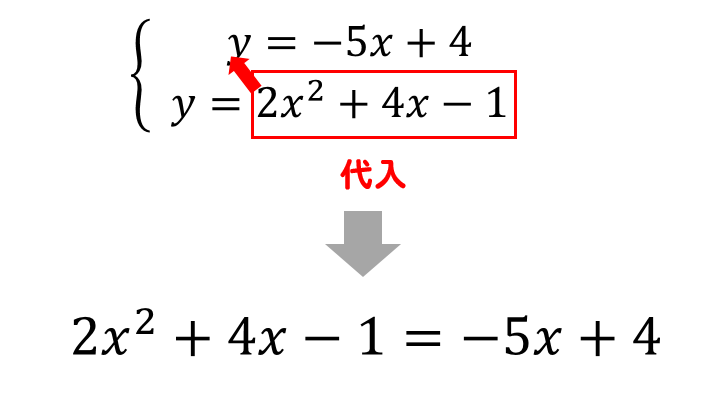
$$2x^2+4x-1=-5x+4$$
$$2x^2+9x-5=0$$
$$(2x-1)(x+5)=0$$
$$x=\frac{1}{2}, x=-5$$
\(\displaystyle{x=\frac{1}{2}}\)のとき
$$y=-5\times \frac{1}{2}+4$$
$$=-\frac{5}{2}+\frac{8}{2}$$
$$=\frac{3}{2}$$
\(x=-5\)のとき
$$y=-5\times (-5)+4$$
$$=25+4$$
$$=29$$
よって、交点はそれぞれ以下のようになります。
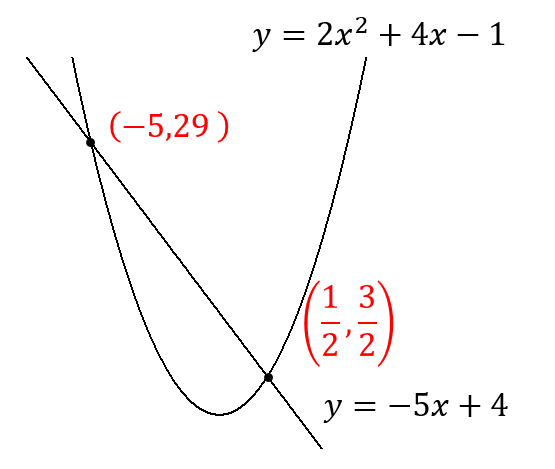
放物線と直線の交点 まとめ
お疲れ様でした!
放物線と直線の交点は
連立方程式を解く!
ですね(^^)
連立方程式を解くときには、二次方程式の解法も必要になってきます。
計算に不安がある方は、方程式の練習もしておきましょう!
【二次方程式】問題の解説付き!解き方をパターン別に説明していくよ!
放物線と直線の交点の求め方!←今回の記事


















中学校3年生の問題の連立の最後の代入のところy=3+6が2つあってy=−2+6の式と解がないですよ
ご指摘ありがとうございました!!
また、何か不備などございましたらご連絡お願い致します(..)
よくわかりました
お役に立てて良かったです^^
とてもわかり易く、学校の予習ができるようになりました。ありがとうございます!
お役に立てて嬉しいです^^