【二次関数】どのように平行移動したら重なる？例題を使って問題解説！

今回解説する問題は、数学Ⅰの二次関数の単元からです。

今回の内容は動画でも解説しています！

サクッと理解したい方はこちらをどうぞ(‘◇’)ゞ

問題を解くためのポイント！

\(x^2\)の係数が等しい放物線は、グラフの形が全く同じということがわかります。

グラフの位置が違うだけですね。

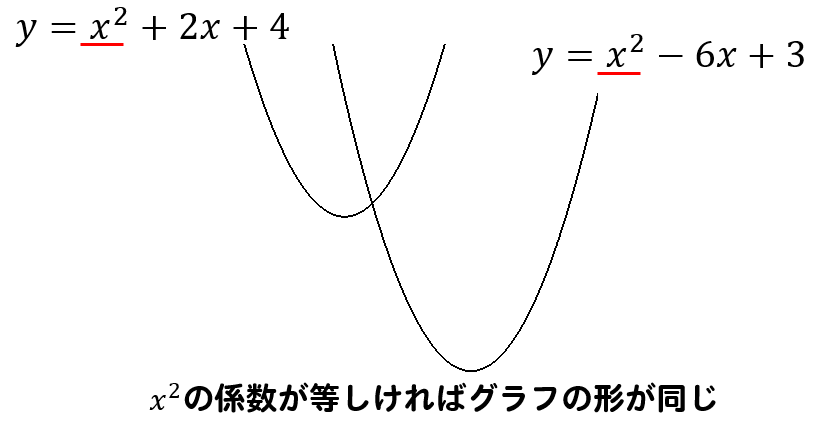
だから

\(y=2x^2+x+3\)と\(y=2x^2+100x-4000\)

こんな見た目が全然違いそうな放物線であっても

\(x^2\)の係数が等しいので、平行移動すれば

それぞれのグラフを重ねることができます。

それでは、どれくらい平行移動すれば

それぞれの放物線を重ねることができるのか。

それは

それぞれの放物線の頂点を見比べることで調べることができます。

例えば

頂点が\((2,4)\)と\((4,-1)\)であれば

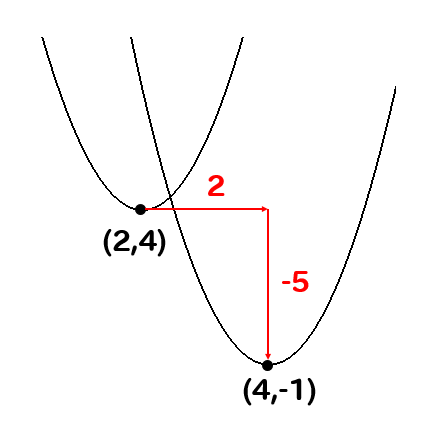
\(x\)軸方向に2、\(y\)軸方向に－5だけ平行移動すれば重ねることができるということが読み取れます。

問題解説！

それでは、先ほどの問題を解いてみましょう。

まずは、それぞれの放物線の頂点を求めてやりましょう。

$$y=x^2+2x+4$$

$$=(x+1)^2-1+4$$

$$=(x+1)^2+3$$

頂点\((-1,3)\)

$$y=x^2-6x+3$$

$$=(x-3)^2-9+3$$

$$=(x-3)^2-6$$

頂点\((3,-6)\)

頂点が求まったら、移動を調べていきます。

頂点\((-1,3)\)を移動して、頂点\((3,-6)\)に重ねるためには

$$3-(-1)=4$$

$$-6-3=-9$$

よって

\(x\)軸方向に4、\(y\)軸方向に－9だけ平行移動すれば重ねることができます。

頂点を比べて、移動を調べるときに

（移動後）ー（移動前）

このように計算してくださいね。

そうじゃないと逆に移動しちゃうことになるから(^^;

それでは、演習問題で理解を深めていきましょう！

演習問題で理解を深める！

まとめ

お疲れ様でした！

今回の問題でおさえておきたいポイントは

• \(x^2\)の係数が等しい放物線は、平行移動で重ねることができる
• 頂点を比べることで、どれくらい移動しているかを調べることができる

という点です。

考え方は特に難しいモノではありません。

ですが、頂点を求める計算が求められます。

そのため、平方完成が苦手な方は

まず頂点を確実に求めれるように練習しておきましょう。

分数が出てくると、平方完成できない…という方はこちらの記事を参考にしてみてくださいね＾＾

＞＞＞【平方完成】分数でくくるパターンの問題の解き方を解説！