【連立方程式】加減法の解き方をわかりやすく問題を使って徹底解説！

今回は、中2で学習する

『連立方程式』の単元から

加減法を使った解き方について徹底解説していくよ！

連立方程式を解いていく上で

必ず必要となってくる基本的な解き方になるから

しっかりとマスターしておきたいね！

がんばって身につけていこう！

今回の記事はこちらの動画でも解説しています(/・ω・)/

加減法の考え方！

加減法を使った解き方とは

簡単に言うと…

足したり、引いたりして文字を消す！

ということです。

連立方程式って、\(x,y\)の２つも謎の文字があってややこしいよね。

これが\(x\)だけ、\(y\)だけであれば簡単なのになぁ…って思います。

それならば！

文字が1種類になるように変形してやればいいじゃん！

ということで

アイツを消せ――――――！！！

ってな感じで、文字を消してやる。

そうすることで簡単に解けるようになるよ！

っていうのが加減法の考え方です。

具体的な解き方については、下で見ていきましょう。

加減法の基本問題

さて、\(x\)と\(y\)の前についている数(符号は気にしない)に注目してみましょう。

\(x\)は、両方とも\(1\)になっています。

\(y\)は、\(2\)と\(1\)になっていて揃っていません。

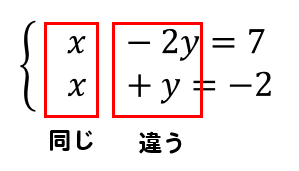
こういう場合、数が揃っている文字というのは

消しやすいヤツ

ということになります。

なので、今回の連立方程式では\(x\)に消えてもらうことにしましょう。

これらは、符号も含めて全く同じモノどうしなので、ひき算をすることによって消すことができます。

$$\LARGE{x-x=0}$$

数が一緒だけど符号が違う場合には

$$\LARGE{x+(-x)=0}$$

このように足し算をしてやることで消してやることができます。

それでは、それぞれの式を引き算することで\(x\)を消してやります。

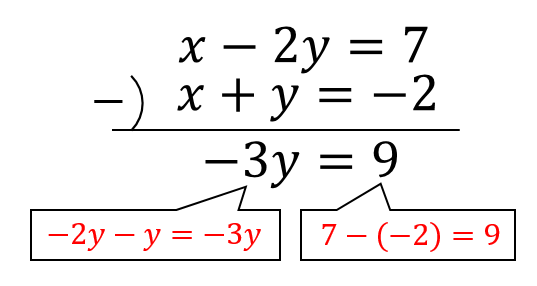
すると、このように\(y\)だけが残った方程式ができあがります。

縦書きの計算が分からない場合には、こちらの記事で確認しておいてね！

あとはこれを解いていきましょう。

$$-3y=9$$

$$y=9\div(-3)$$

$$y=-3$$

すると、\(y\)の値を求めることができました。

次は、\(x\)の値を求めましょう。

先ほど求めた\(y\)の値を

連立方程式で与えられた2本の式のうち

見た目が簡単そうな式に代入してやります。

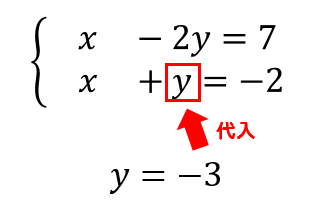
今回は、\(x+y=-2\)に\(y=-3\)を代入します。

すると

$$x-3=-2$$

$$x=-2+3$$

$$x=1$$

このようにして、\(x\)の値も求めてやります。

よって答えは

となりました。

加減法の手順としては以下の通りです。

加減法の係数が違うパターン

この連立方程式では、\(x\)と\(y\)の前についている数を見ても…

どちらも揃っていませんね

これでは、足しても引いても文字を消してやることができません。

こういうときには、文字の前にある数が同じになるよう

式を何倍かしてやれば良いです！

分数の分母を揃えるために通分したときを思い出してもらえるといいです。

\(x\)の文字を消したい場合には

それぞれの数、3と2の最小公倍数である6に揃えていきましょう。

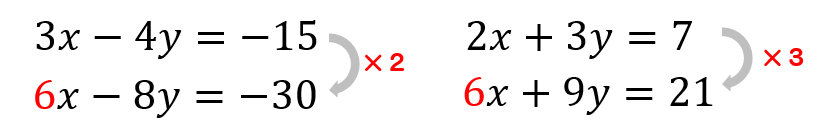
こうして変形した式を連立方程式として解いていきます。

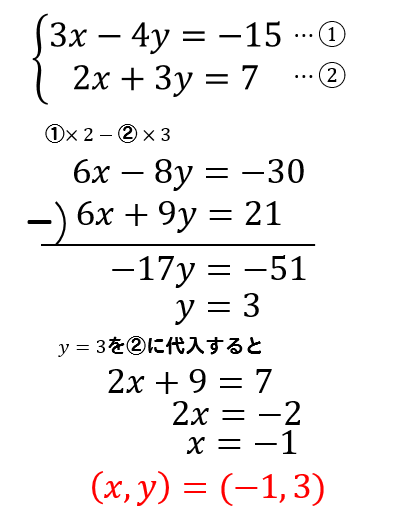
\(y\)の文字を消したい場合には

それぞれの数、4と3の最小公倍数である12に揃えていきましょう。

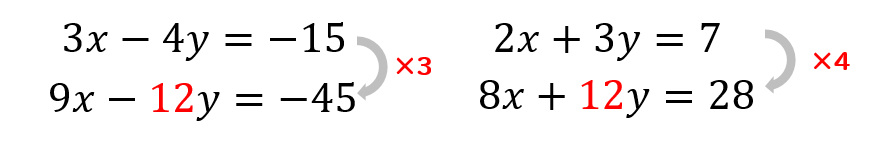
こうして変形した式を連立方程式として解いていきます。

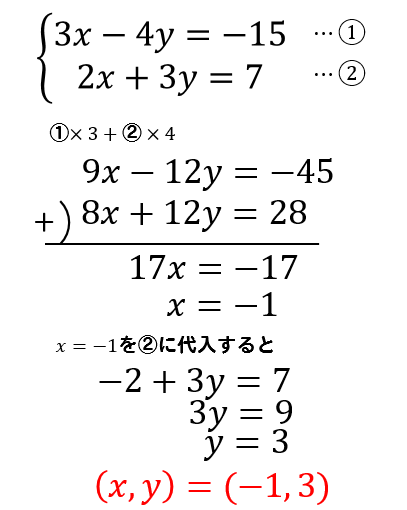
もちろん！

\(x\)と\(y\)のどちらを揃えても同じ答えが出てくるので

自分が計算しやすいと思う方でやっていくようにしましょう。

文字の係数が揃っていなければ

式を何倍かして、数を揃えろ！

【追加演習プリント】自宅学習で伸ばしたい方へ！

この記事を読んでくださっている保護者さんの方へ！

ここで紹介してる例題を一通り理解してもらえれば、加減法の解き方はバッチリです＾＾

あとは実戦演習を通して、手本がなくてもスラスラと解けるようにしておいてもらいたいです！

というわけで、自宅学習で活用してもらいたい演習プリントを用意しました。

ここで取り上げている問題はこちら！

すべて入試問題からピックアップしてみました！これが全部解ければ自信になりますね＾＾

というわけで、これらの演習問題＆解説をプリント形式で用意しているので、印刷してお子さんに渡してあげてください。

10分ほどで取り組める分量になっているので、スキマ時間を活用して加減法の理解度を高めておきましょう！

勉強のスタート時に小テストとして取り組んでみると、イイ感じに集中力が高まって、その日の学習がスムーズになってくるかもしれませんね(‘ω’)ノ

追加演習をやってテストの点数をUPさせたい方には、課題プリントをメールで送らせてもらっています。

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

連立方程式　加減法の解き方　まとめ

お疲れ様でした！

加減法を使った解き方は分かりましたか？

数が揃っている文字を消す！

というのがポイントでしたね。

同じ符号どうしであれば引き算

異なる符号どうしであれば足し算

をすることによって文字を消してやることができます。

文字の前にある数が揃っていない場合には

式を何倍かして数を揃えるようにしましょう。

そのときには、\(x\)と\(y\)のうち

自分が計算しやすいと思う方を揃えるようにしてくださいね！

なるべく楽に計算したいもんね(^^)

連立方程式の加減法をマスターできたら

次は代入法！

それぞれの解き方がマスターできたら

ひたすら演習問題だ！

ファイトだ(/・ω・)/