【連立方程式】3つの文字、式の問題を計算する方法は？

今回取り上げる問題はこちら！

 

高校数学で良く出てくる連立方程式ですね。

二次関数や円の式を作るときに活用します。

 

このように文字が３つ、式も３つある場合

どのように計算すれば良いのでしょうか？？

 

解き方の手順を解説していきますね(^^)

 

[スタセミ中2バナー]

文字を１つ消して、2つの式を作る

文字が３つのままだと計算ができません＞＜

ということで、文字を１つ消しましょう！

文字を消すときには、なるべく係数が揃っている文字に注目しましょう。

今回の連立方程式では、\(z\)の係数が揃っているので\(z\)の文字を消していきます。

 

 

どうやって文字を消すかというと

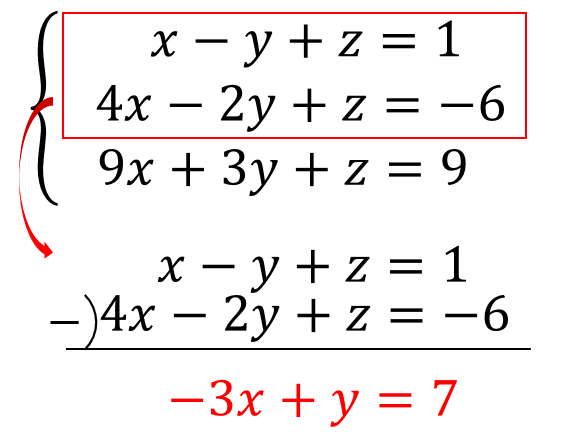
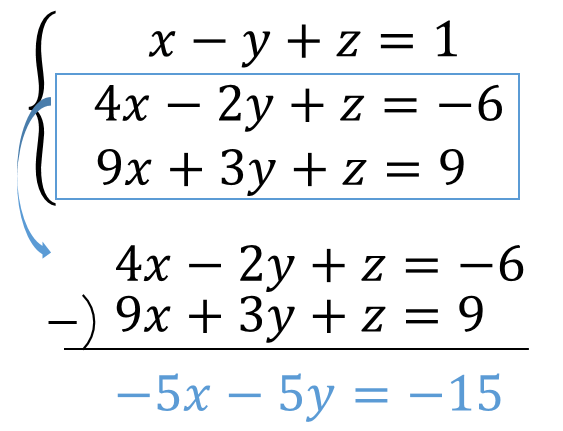
このように3つの式から、２つずつ式を組み合わせて加減法で消していきます。

 

 

すると新たに\(x,  y\)だけの式が２つできましたね！

$$-3x+y=7$$

$$-5x-5y=-15$$

 

2つの式を連立方程式で解く

先ほど作った２つの式を連立方程式で解いていきましょう。

$$\large{\begin{eqnarray} \left\{ \begin{array}{l}-3x+y=7 \dots①\\-5x-5y=-15 \dots②\end{array} \right. \end{eqnarray}}$$

 

文字が2つになったので、これは中学で学習した加減法を使えば簡単に解くことができますね！

今回の連立方程式では②の式の両辺を\((-5)\)で割ると\(y\)の係数を揃えることができます。

$$(-5x-5y)\div(-5)=-15\div (-5)$$

$$x+y=3$$

 

よって、加減法を用いると

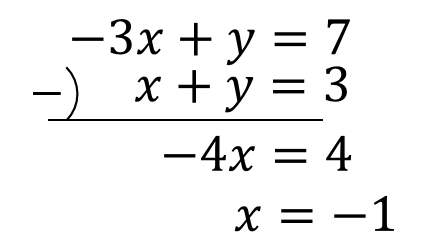
\(x=-1\)の値が求まります。

次に\(x=-1\)を\(x+y=3\)に代入すると

$$-1+y=3$$

$$y=4$$

 

これで\(x,  y,  z\)の3つの文字のうち2つの値が求まりました。

残りの１つを求める

２つの文字の値が求まったら

元の連立方程式に代入して、残り１つの文字の値を求めましょう。

\(x=-1,  y=4\)を\(x-y+z=1\)に代入します。

 

$$-1-4+z=1$$

$$z=1+5$$

$$z=6$$

 

以上より

$$x=-1$$

$$y=4$$

$$z=6$$

となります。

完成！！

 

少し手間ではありましたが、解き方は難しいものではありませんでしたね。

もう一度、手順を確認しておきましょう。

 

それでは、理解を深めるために演習問題に挑戦してみましょう！

この連立方程式が活躍する二次関数の問題で実践してみよう。

3点を通る二次関数の式を求める問題

 

 

まとめ

お疲れ様でした！

３つの文字、式の連立方程式を解くためには

まず、文字を１つ消してやることがポイントでしたね！

 

そうすることで今まで解いてきた連立方程式と同じ形を作ることができます。

たくさん練習して、しっかりと手順を身につけておこうね(^^)

ファイトだー(/・ω・)/