【平方完成】分数でくくるパターンの問題の解き方を解説！

今回は高校数学Ⅰで学習する『二次関数』の単元から

分数でくくるパターンの平方完成について解説していくよ！

こんなやつだね。

分数が出てくると解けなくなっちゃう人が多いから

今回の記事を通して、しっかりとやり方をマスターしていきましょう！

今回の記事は、こちらの動画でも解説しています(/・ω・)/

平方完成の基本的なやり方

まずは平方完成の基本的なやり方を確認しておきましょう。

例えば

$$\LARGE{y=2x^2+4x+3}$$

この式を平方完成してみましょう。

平方完成の手順

• \(x^2\)の係数で、\(x^2\)と\(x\)の項をくくってやります。

 

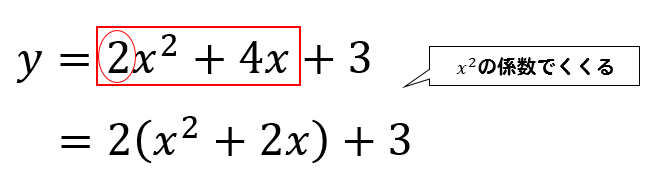
• \(x\)の項の係数を半分にして、その数の二乗を引きます。

 

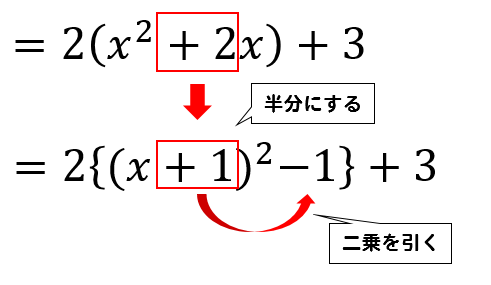
• くくっていた数を分配法則で計算してやれば完成！

このような手順で平方完成をしていきます。

それでは、分数が出てくるパターンの平方完成を上の手順に沿って解いていきましょう。

分数でくくる平方完成の解き方

$$\LARGE{y=\frac{2}{3}x^2-2x+3}$$

まずは、\(x^2\)の係数である\(\displaystyle \frac{2}{3}\)でくくってやります。

$$\LARGE{y=\frac{2}{3}(x^2-3x)+3}$$

このような式ができあがります。

おいおい…

分数でくくるの難しいんだけど。

そこんとこもう少し詳しく教えてくれいや

確かに！

分数の平方完成が苦手な人は

この部分で間違えている人が多いですからね(^^;)

分数のくくり方を詳しく説明しておきましょう。

くくりだすという計算は割り算です。

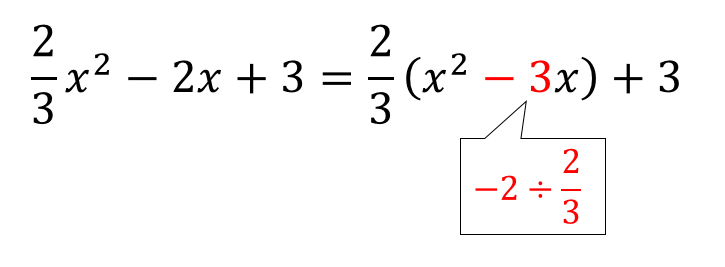
式変形したいところを

くくりだす数で割ってやればOKです。

分数だと暗算が難しいので

わり算の式をちゃんと書いて計算してやれば大丈夫！！

いやぁ…分数の割り算は嫌だな…という方は

通分を利用して、くくりだしてやることもできます。

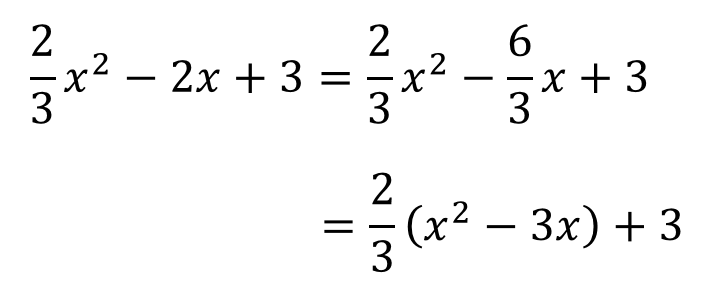
このようにくくりだしたい部分を通分してやると

式変形がしやすくなりますね。

分数のくくりだしができたら

\(x\)の項を半分にして、二乗を引きます。

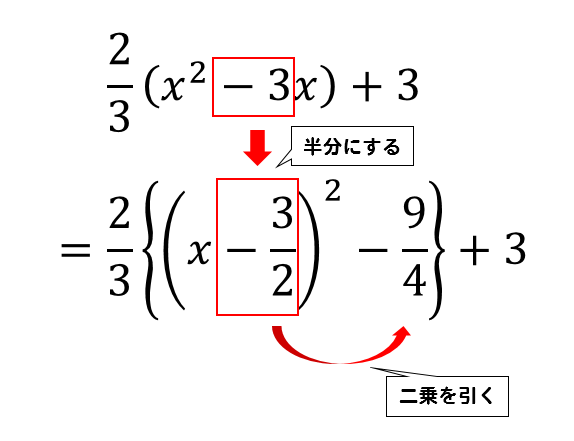
半分にするというのは、\(\displaystyle \times \frac{1}{2}\)をするということですね。

最後に、分配法則を利用して計算してやりましょう。

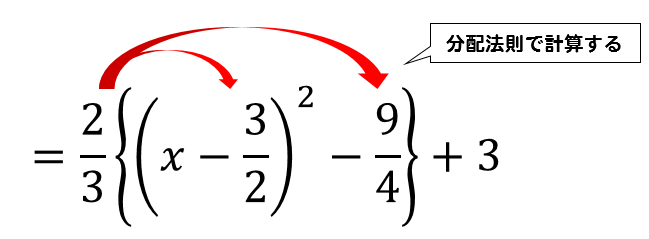
$$\Large{=\frac{2}{3} \left( x-\frac{3}{2} \right)^2-\frac{3}{2}+3}$$

$$\Large{=\frac{2}{3} \left( x-\frac{3}{2} \right)^2-\frac{3}{2}+\frac{6}{2}}$$

$$\Large{=\frac{2}{3} \left( x-\frac{3}{2} \right)^2+\frac{3}{2}}$$

少し複雑な式変形にはなりますが

このように分数の式を平方完成することができます。

やり方がわかったら

演習問題を通して理解を深めていきましょう。

演習問題で理解を深める！

分数でくくる平方完成　まとめ

お疲れ様でした！

分数の平方完成は、くくりだしが上手くできるようになれば

あとは、丁寧に計算していくだけで解くことができるようになります！

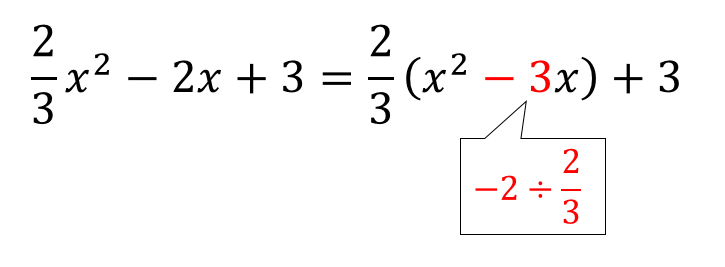
このようにわり算を丁寧に計算しながらくくりだすか

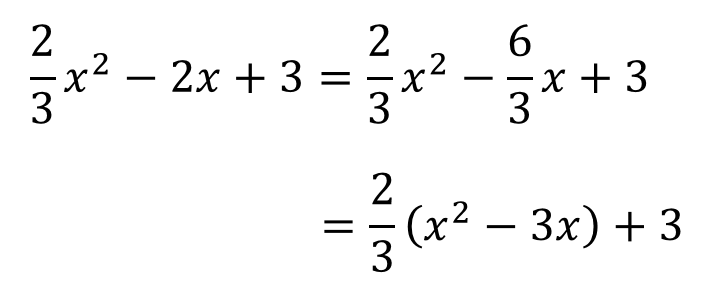
通分を利用すれば暗算でもくくりだしができるようになります。

自分に合うほうでやっていきましょう。

私は通分でやるのが好きです。

こっちの方がミスが少ないような気がします(^^)

たくさん演習問題をやってみて

確実に平方完成ができるようになるまで頑張っていきましょう！

ファイトだー(/・ω・)/