今回は高校数学Ⅰの三角比という単元から
「三角比の値を求める方法」
についてイチから解説していきます。
ここの単元では、サイン、コサイン、タンジェント!!
という魔法の呪文みたいな言葉が出てきますw
聞いたことあるけど、意味わかんねぇ…
って思っている方も多いと思いますので
今回の記事では、そんな三角比をイチから解説していきます。
数学が苦手だ…という方に向けて初歩から進めていくぞ!
今回の内容はこちらの動画でも解説してるよ( `ー´)ノ
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
三角比(サイン、コサイン、タンジェント)とは
三角比とは、一言で言うと…
直角三角形の辺の比
のことをいいます。
直角三角形の辺の比、省略して三角比!
と覚えておけばよいね(^^)
結論を最初に書いておくと、こんな感じです。
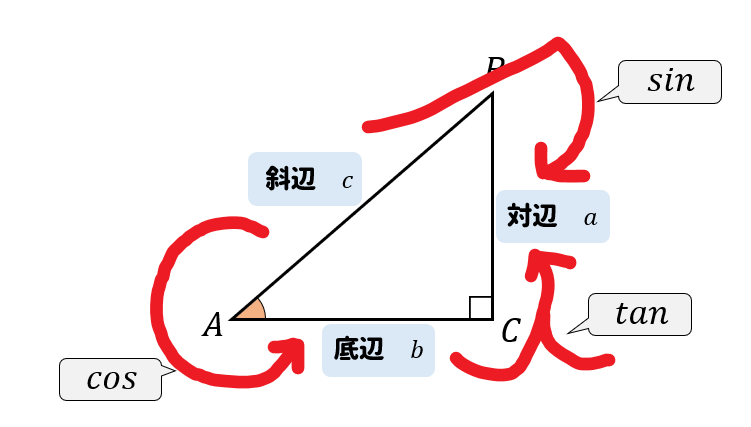
$$\sin A =\frac{a}{c}$$
$$\cos A=\frac{b}{c}$$
$$\tan A=\frac{a}{b}$$
斜辺と対辺の比をとって、分数の形で表した値を\(\sin\)(正弦)といいます。
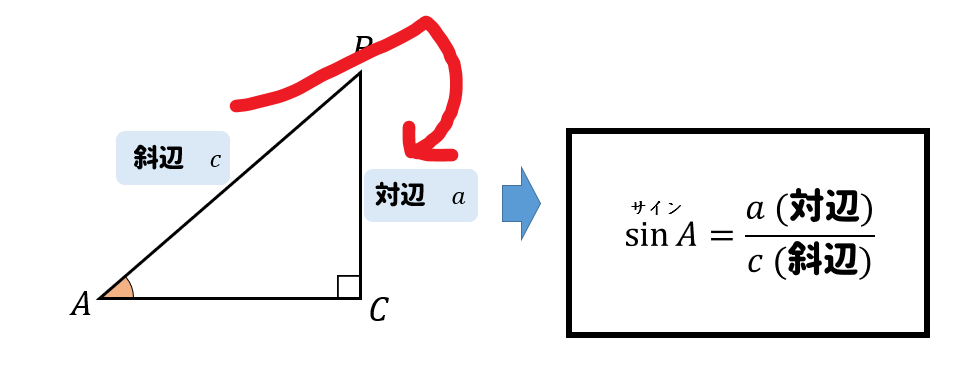
斜辺と底辺の比をとって、分数の形で表した値を\(\cos\)(余弦)といいます。
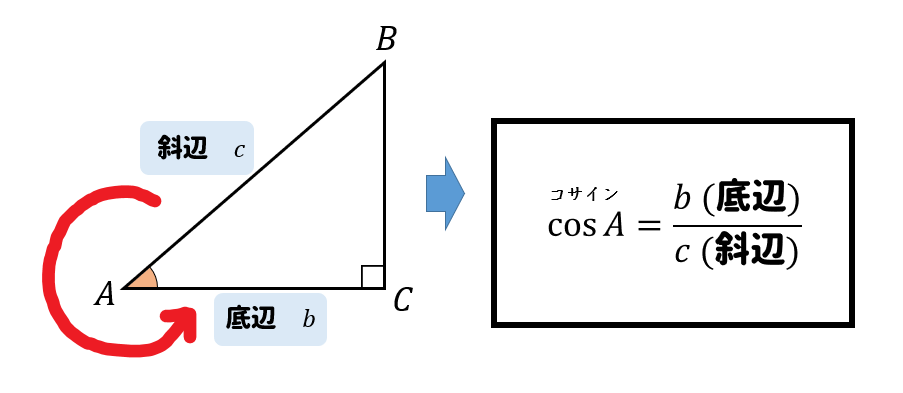
底辺と対辺の比をとって、分数の形で表した値を\(\tan\)(正接)といいます。
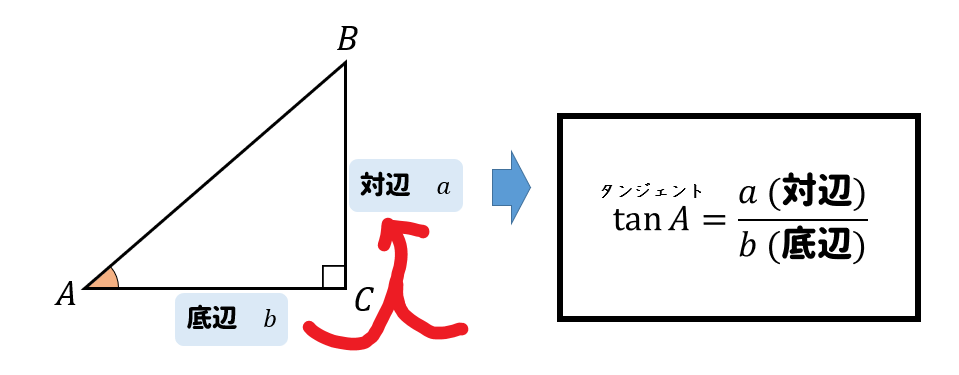
でも、ここで1つ疑問が湧いてくるね…
なぜこんなことを考えないといけないのか!!

マッチョくんが言っているように
直角三角形の辺の比である三角比を扱うことで、いろんなことがラクになるんだ。
図形の辺の長さを求めたり、面積を求めたり…
普通の計算では、とっても面倒なものをサクッと計算してくれるんだ。
とってもありがたい存在だよね!
なので、そんな三角比!
これからとっても重宝していくことになるので
斜辺と底辺の比は、コサイン。
斜辺と対辺の比は、サイン。
底辺と対辺の比は、タンジェント。
というように、それぞれには特別な名前をつけて扱っていくんだよ。
三角比の値の求め方!
【問題】
次の直角三角形\(ABC\)において、\(\sin A\)、\(\cos A\)、\(\tan A\) の値を求めよ。
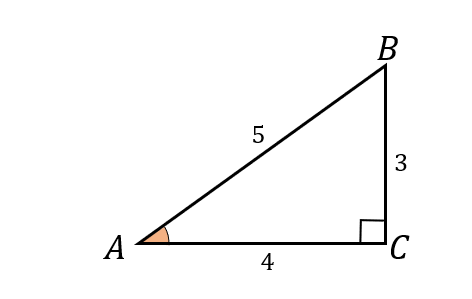
それぞれどこの辺を比較すればよいのかを覚えておけば簡単に解くことができます。
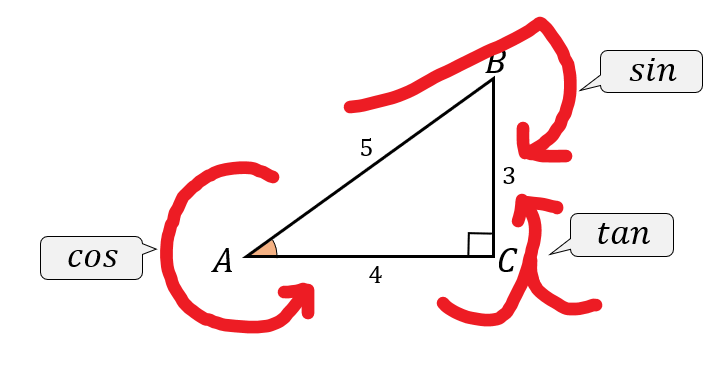
$$\cos A=\frac{4}{5}$$
$$\sin A=\frac{3}{5}$$
$$\tan A=\frac{3}{4}$$
簡単ですね!
ただし、位置関係は覚えておかなければなりませんよ!!
次!
【問題】
次の直角三角形\(ABC\)において、\(\sin A\)、\(\cos A\)、\(\tan A\) の値を求めよ。
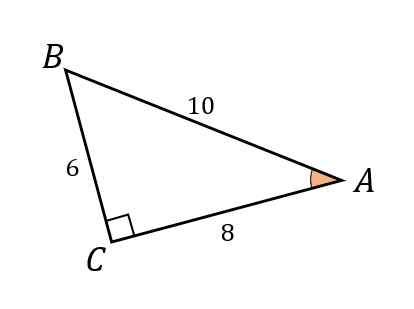
あれ、斜めっている…
それに∠Aが右側にある。
このままでは、どこを比較していけばよいのかが分かりにくい。
こういうときには

このように、直角三角形を見やすい形に変形しましょう。
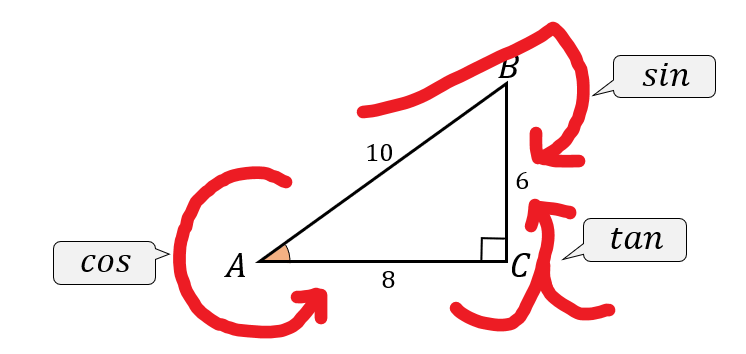
$$\cos A=\frac{8}{10}=\frac{4}{5}$$
$$\sin A=\frac{6}{10}=\frac{3}{5}$$
$$\tan A=\frac{6}{8}=\frac{3}{4}$$
約分できる場合には忘れないようにね!
次だ!
【問題】
次の直角三角形\(ABC\)において、\(\sin A\)、\(\cos A\)、\(\tan A\) の値を求めよ。
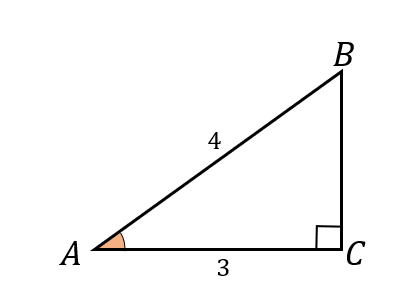
おや…辺BCの長さが書いていませんね。
でも、これはミスではありません。
ちょっとしたイジワル問題なのです。
直角三角形では、三平方の定理というものを使えば
2辺から残り1辺の長さを求めることができましたね。

というわけで、イジワル問題で辺の長さが書いていない場合には三平方の定理を使って、辺の長さを求めていきましょう。
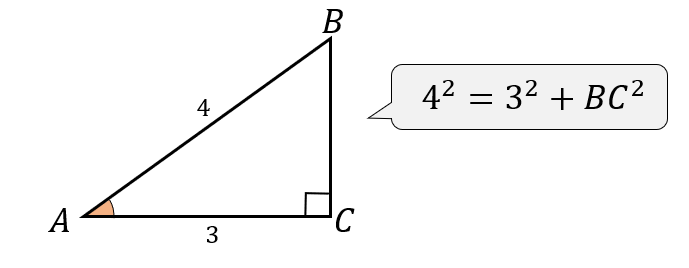
$$\begin{eqnarray}4^2&=&3^2+BC^2\\[5pt]16&=&9+BC^2\\[5pt]BC^2&=&7\\[5pt]BC&=&\sqrt{7} \end{eqnarray}$$
辺の長さが求まったら、あとは楽勝ですね(^^)
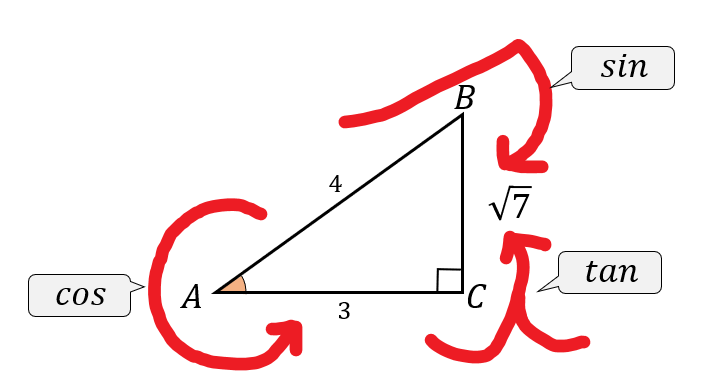
$$\cos A=\frac{3}{4}$$
$$\sin A=\frac{\sqrt{7}}{4}$$
$$\tan A=\frac{\sqrt{7}}{3}$$
30°、45°、60°の三角比の値
これまでは直角三角形の辺の長さを比べながら三角比の値を求めてきました。
先ほどの問題で実感した通り、3つの辺の長さを求めないと三角比の値が分かりませんでしたね。
しかし、この章のタイトルにあるように
30°、45°、60°を基準と考えた直角三角形では
辺の長さを求めずとも三角比の値を求めることができます。
覚えていますでしょうか。
これらの角を持つ直角三角形には、特別な辺の比がありましたね。

この比を覚えておくだけで
実際の長さを調べくことなく三角比の値を求めることができます。
具体的には以下のようになります。
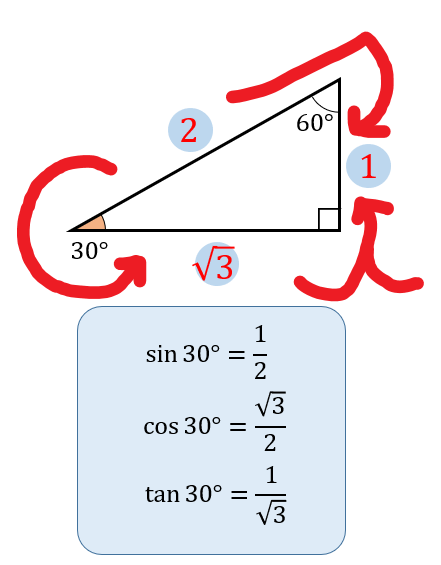
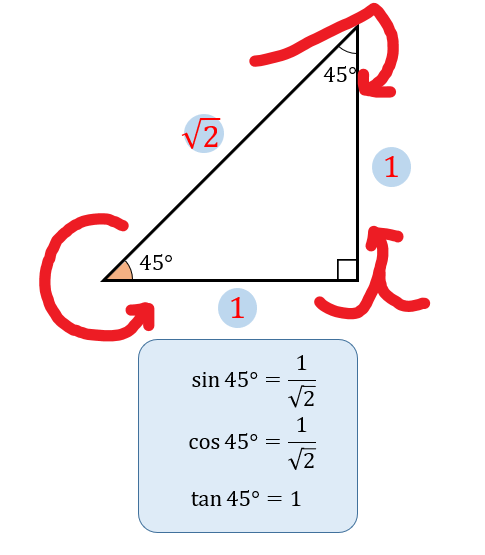
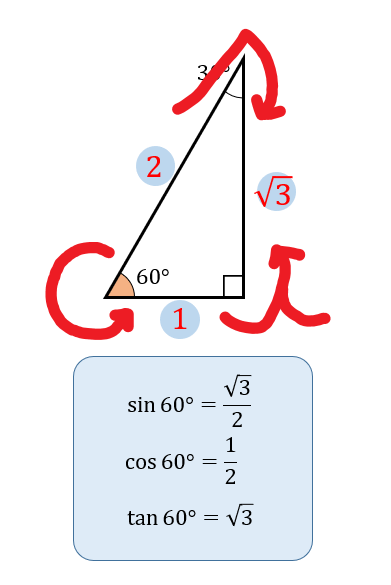
今後の問題では、30°、45°、60°の三角比を使って展開されていきます。
まずはそれぞれの三角形の辺の比を覚えること
そして、三角比の比べる辺の位置を覚えること
この2つを徹底していきましょう。
これは絶対に覚えておきたいので表でまとめておきますね。
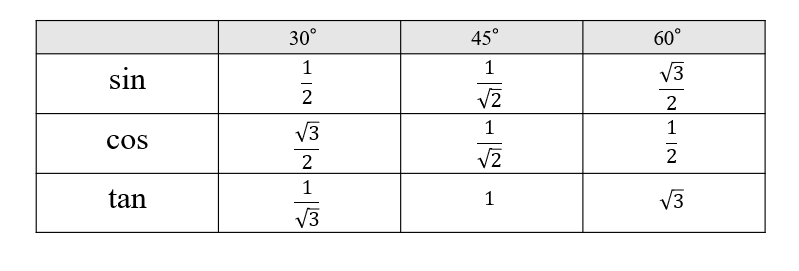
三角比の値まとめ!
お疲れ様でした!
今回学習した内容は、今後三角比を進めていく上で土台となってくるものです。
疑問点がなくなるまで、たくさん問題を解いて理解を深めておきましょう!
ファイトだ(/・ω・)/



















最初の図、a分のcではなく、c分のaじゃないですか?
訂正しました!
ご指摘ありがとうございますm(__)m
めっちゃ分かりやすいです!!ありがとうございます
参考にしてもらえて嬉しいです^^
ありがとうございます。
高専一年目で少しつまづいていましたができるようになりました
お役に立てて良かったです!
高専の内容は難しいですが
1つずつがんばっていってください^^