今回の記事では、
分数、小数、ルート、置き換え、絶対値を含む二次方程式など
ちょっと複雑な二次方程式の解き方についてまとめていきます。
二次方程式の基礎問題についてはこちら!
小数を含む二次方程式
【例題】次の二次方程式を解け。
$$0.2x^2-0.5x-1.2=0$$
小数は両辺を10倍、100倍して小数を消しましょう。
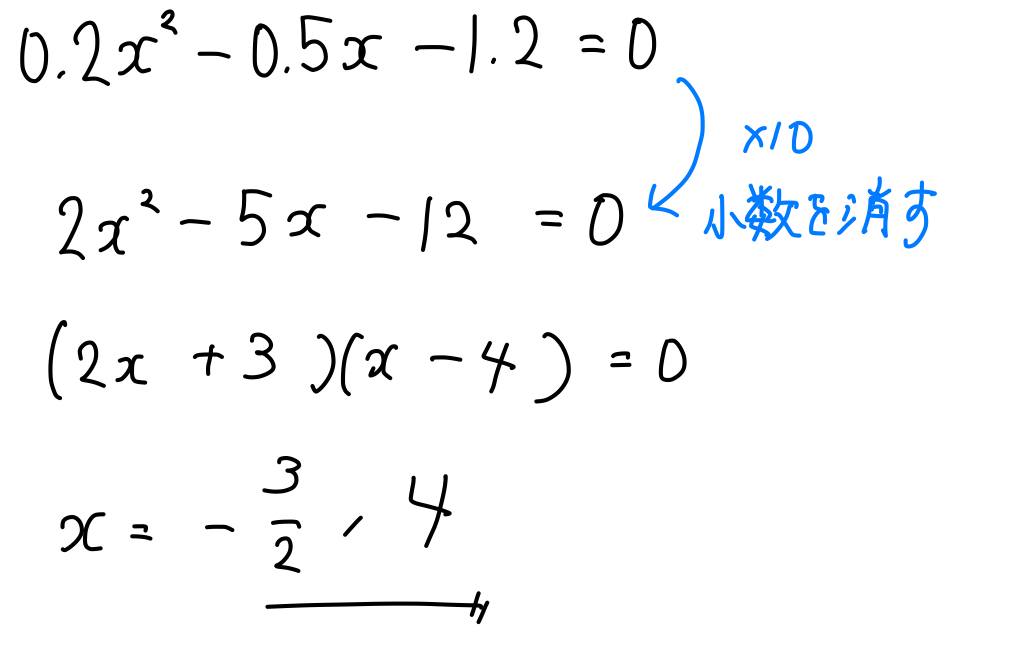
分数を含む二次方程式
【例題】次の二次方程式を解け。
$$\frac{x^2-1}{3}-\frac{2x-3}{4}=\frac{x^2+5}{6}$$
分数が出てきたときには、
分母の最小公倍数を両辺に掛けて、分数を消すようにしましょう。
分子が多項式になっている場合には、かっこをつけることも忘れないように!
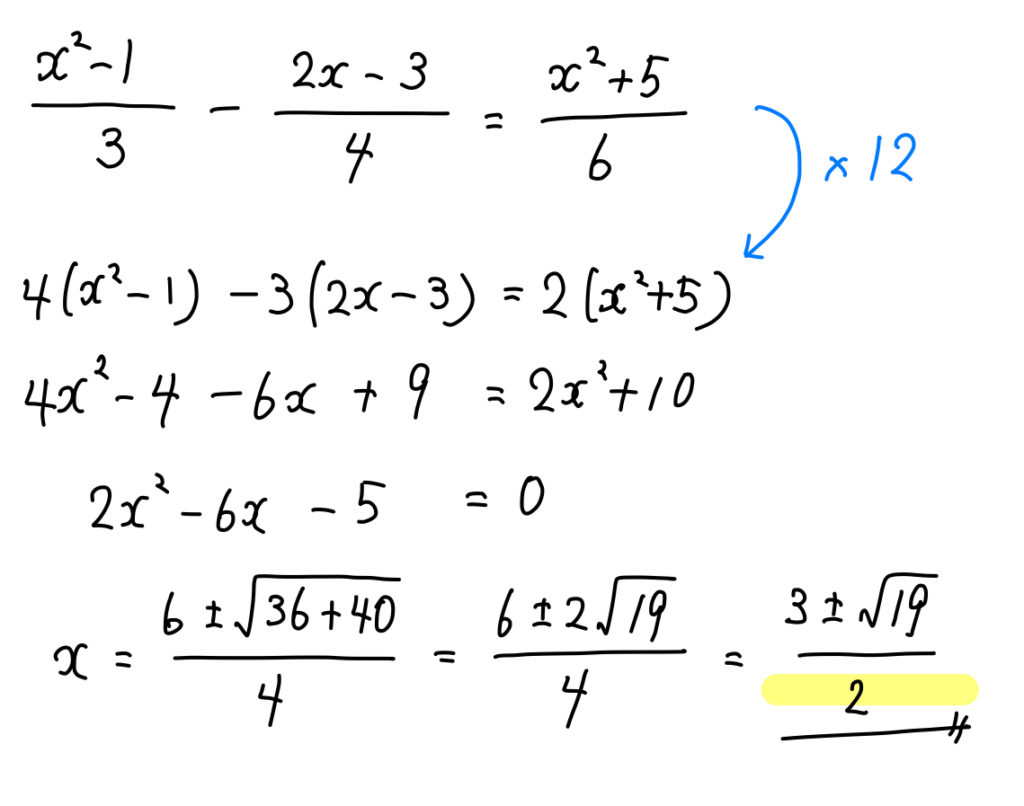
【練習問題】次の二次方程式を解きなさい。
(1)\(\frac{2}{3}x^2-\frac{1}{6}x-\frac{1}{2}=0\)
(2)\(\frac{1}{3}x^2-\frac{5}{2}x+1=0\)
(3)\(-0.5x^2-\frac{3}{2}x+10=0\)
ルートを含む二次方程式
【例題】次の二次方程式を解け。
$$x^2-2\sqrt{3}x+3=0$$
ルートを含む場合には、因数分解ができる場合もありますが、
基本的には「解の公式を利用する」ことが多いですね。
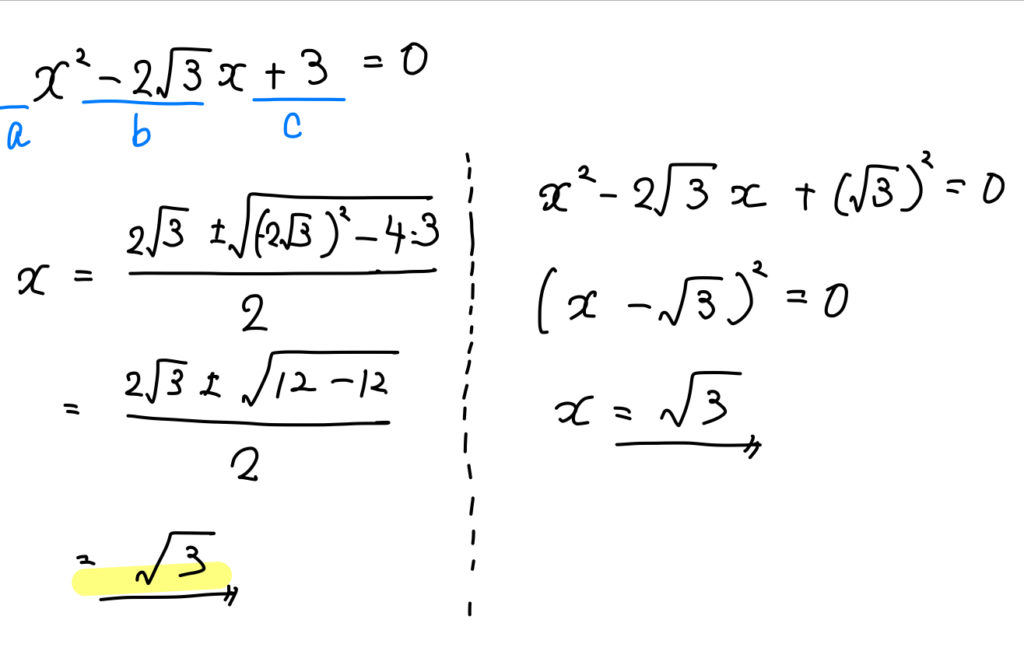
【例題】次の二次方程式を解け。
$$\sqrt{3}x^2-4x-2=0$$
解の公式を利用する場合には、ルートの中にルートが残ってしまう場合があります。
その場合には、二重根号がはずせないか考えてください。
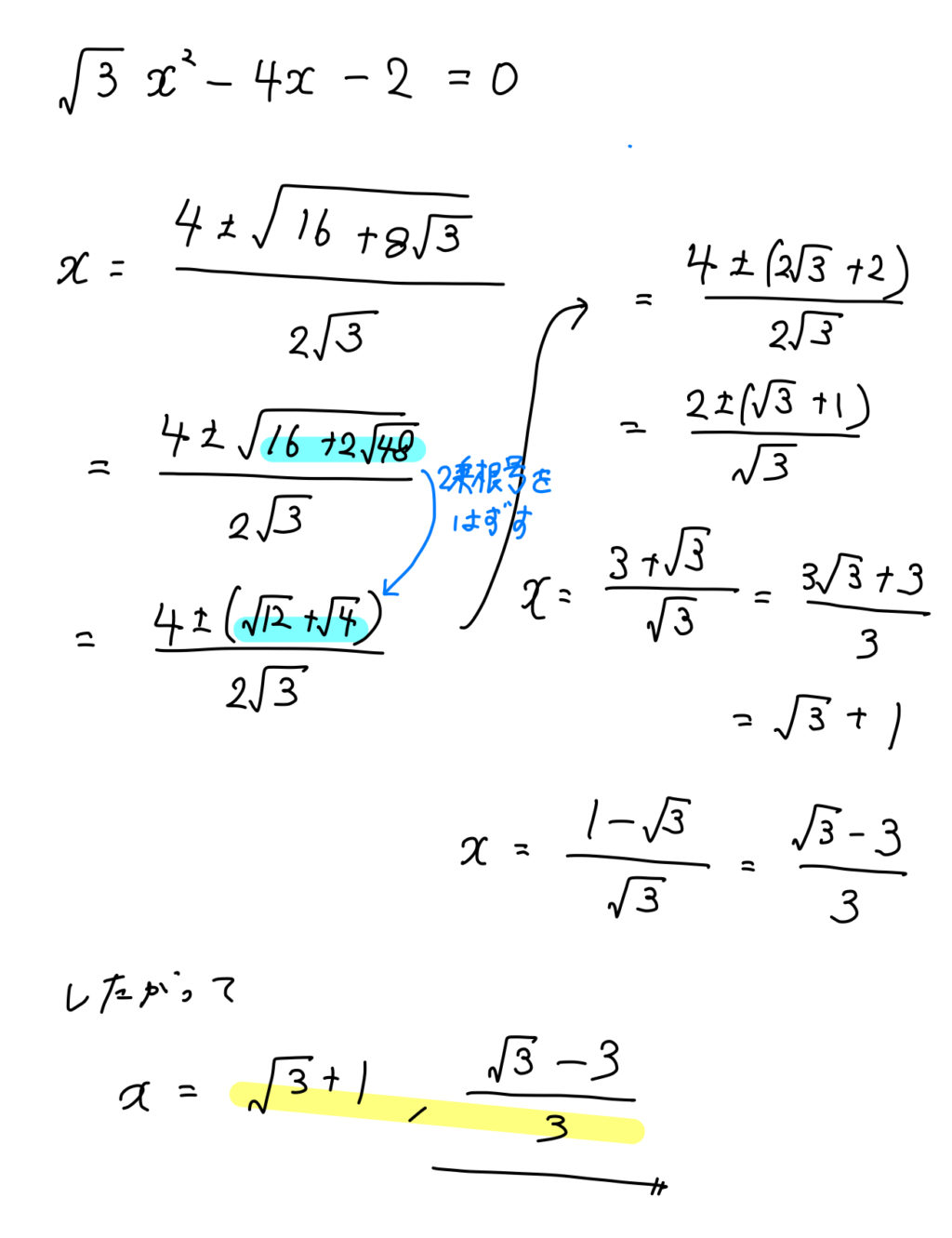
【練習問題】次の二次方程式を解きなさい。
(1)\(x^2-\sqrt{2}x-1=0\)
(2)\(2x^2+2\sqrt{3}x+1=0\)
(3)\(4x^2-2\sqrt{2}x-1=0\)
(4)\(2x^2-4\sqrt{3}x+6=0\)
(5)\(\sqrt{3}x^2-4x-2=0\)
置き換えを利用する二次方程式
【例題】次の二次方程式を解け。
$$(x-6)^2-(x-6)-5=0$$
方程式の中に同じ部分があれば、置き換えを利用していきましょう。

【練習問題】次の二次方程式を解け。
$$2(x+2)^2-(x+2)-3=0$$
絶対値を含む二次方程式
【例題】次の二次方程式を解け。
$$x^2-|x-1|-3=0$$
絶対値は場合分けをしていきましょう。
絶対値の中身が0以上になる場合 ⇒ 絶対値をそのままはずす。
絶対値の中身が負になる場合 ⇒ マイナスをかけてはずす。
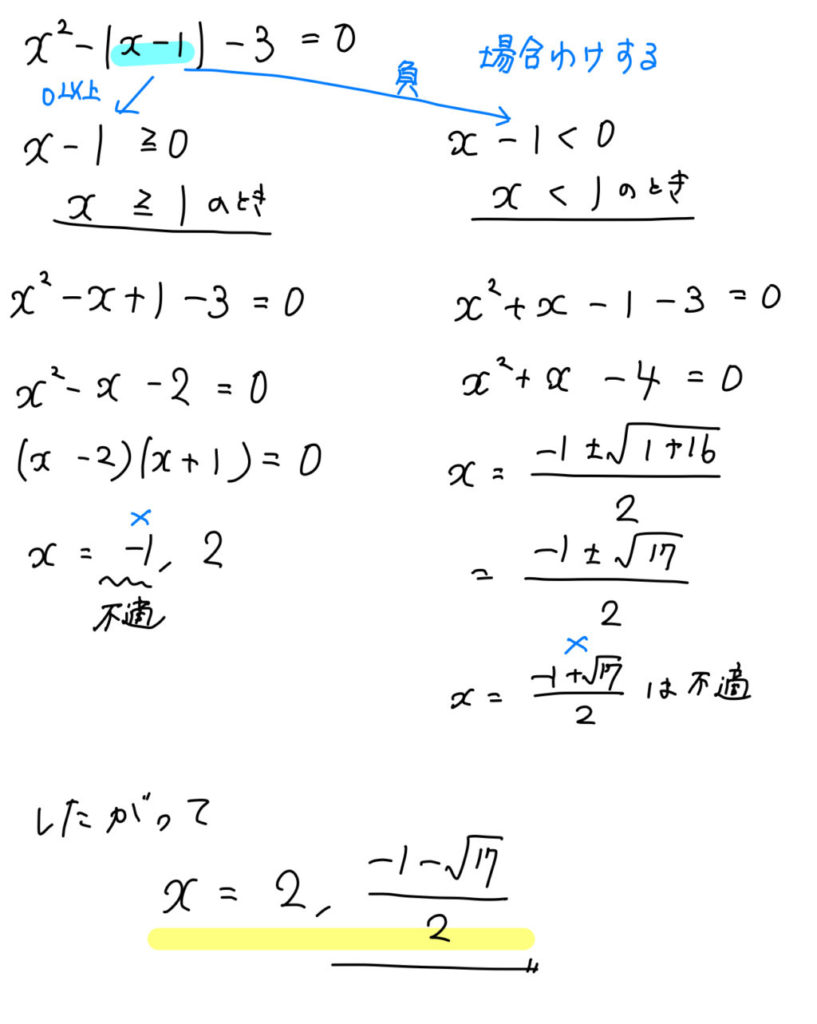
【練習問題】次の二次方程式を解け。
(1)\(x^2-2|x|-3=0\)
(2)\(x^2+x+|x-1|=5\)
まとめ!
お疲れ様でした!
いろんなパターンがありましたが、練習問題を通してそれぞれの解き方を身につけておきましょう。
計算が複雑になっているモノが多いので、途中式をていねいに書いていくようにしましょうね(/・ω・)/
- 一次関数の定義域、値域とは?問題の解き方を解説!
- 頂点の求め方、公式は?問題を使ってイチから解説!
- 平方完成!分数でくくるパターンの問題の解き方を解説!
- 平方完成!文字を含む式の場合は?やり方を丁寧に解説!
- 二次関数グラフの書き方を初めから解説!
- 二次関数の式の作り方をパターン別に解説!
- 二次関数を対称移動したときの式の求め方を解説!
- 平行移動したものが2点を通る式を作る方法とは?
- どのように平行移動したら重なる?例題を使って問題解説!
- 二次関数の最大・最小の求め方をイチから解説していきます!
- 場合分け!最大最小の応用問題の解き方をイチから解説!
- 2変数関数の最大・最小の求め方、パターン別の解説!
- 二次関数の文章題!高校で学習する問題をパターン別まとめ!
- 分数、小数、ルートを含む二次方程式の解き方まとめ! ←今回の記事
- 高校数学で学習する連立方程式の解き方まとめ!
- 文字係数の方程式の解き方まとめ!
- 判別式Dを使って解の個数を調べてみよう!
- 2次方程式の共通解、kの値の求め方はどうやる??
- x軸との共有点、グラフの位置関係を考える問題を解説!
- 係数の符号の決定、グラフから符号を決めるポイントを解説!
- x軸から切り取る線分の長さの求め方と公式!
- 放物線と直線の交点の求め方!
- 二次不等式の解き方を簡単に!高校数学をマスターしよう!
- 文字係数の2次不等式の解き方!場合分けの考え方は??
- 解からの係数決定!グラフの形と座標に注目せよ!
- 絶対不等式!パターン別の例題を使って解き方を解説!
- 2次方程式の解の存在範囲!判・軸・端の条件を見極めるのが重要!
- 4次不等式の解き方を例題解説!
- f(x) > g(x)となる範囲「すべての」「ある」の違いを理解しておこう!
- 絶対値のついたグラフを書いてみよう!



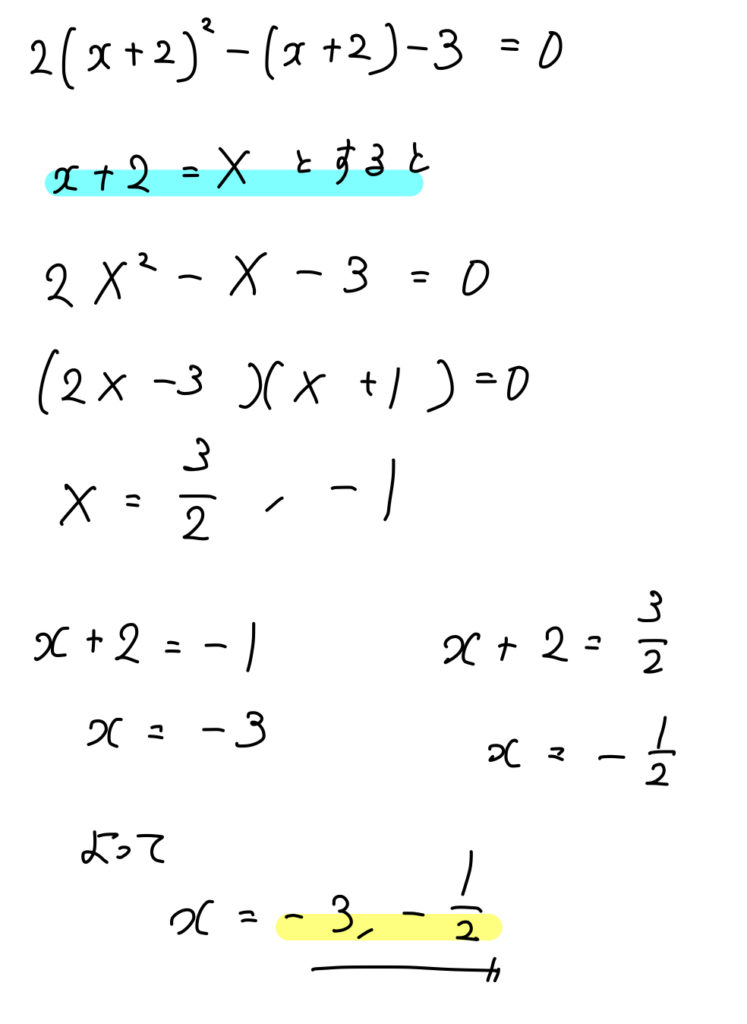















コメントを残す