【反比例】x,y座標がともに整数となる点の個数は？？

中1で学習する比例・反比例の単元から

「反比例の座標がともに整数となる点の個数」

について解説していきます。

 

比例定数の約数に注目する！

というのがポイントですよ(/・ω・)/

【反比例】\(x,y\)座標がともに整数となる点の個数

 

反比例のグラフとは、双曲線の形になっています。

そして、\(x,y\)座標がともに整数となる点とは、

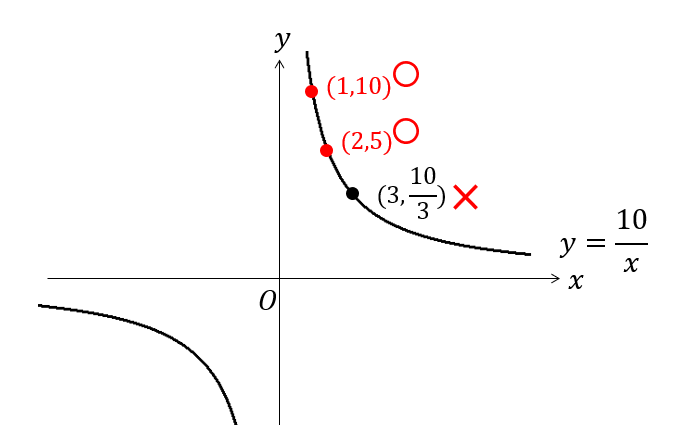
このような点のことをいいます。

 

では、ともに整数となる点に共通している特徴とは…？

\(x\)座標が比例定数の約数になっている

という点です。

 

つまり、ともに整数になる点の個数と求めるためには、

比例定数の約数がいくつあるかに着目することが大事です。

 

今回の問題であれば、

比例定数\(10\) の約数は、\(1,2,5,10\) の計4つあります。

座標で表すと、\((1,10)\), \((2,5)\), \((5,2)\), \((10,1)\) ですね。

 

 

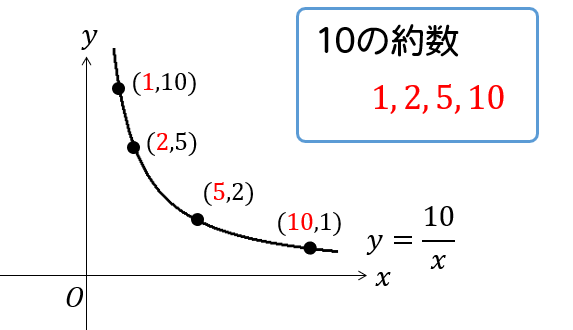
そして、忘れてはならないのが

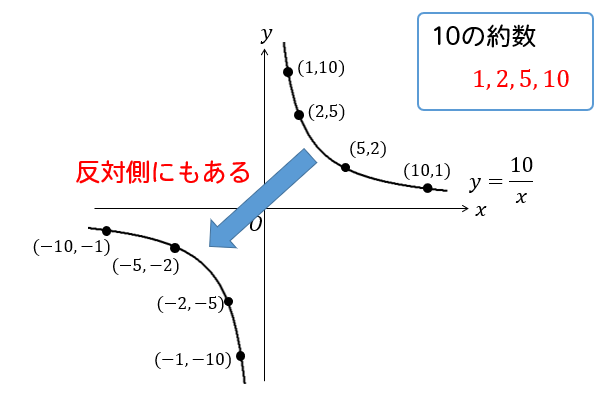
このように反対側にも同じように整数となる点があるはずです。

 

したがって、

求める点の個数は全部で、\(8\)個となります。

 

 

練習問題に挑戦！

 

 

まとめ！

お疲れ様でした！

今回の問題は入試によく出題される重要な問題の1つです。

ですが、ポイントをおさえておけば

誰でも簡単に解けるラッキー問題でもあります。

今回の記事を通して、しっかりと解けるように練習しておいてくださいね(/・ω・)/

 

成績を上げて、志望校合格を勝ち取りたい中3生の方！

数スタの無料メルマガ講座で合格を勝ち取りませんか？

今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！

数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！