【数学Ⅰ】一次関数の定義域、値域とは？問題の解き方を解説！

高校数学Ⅰで学習する二次関数の単元から

「一次関数の定義域、値域」

についてイチから解説していきます。

 

この記事を通して、

定義域が与えられたときのグラフの書き方、値域の求め方

そして、定義域と値域が与えられたときの式の決定について学んでいきましょう。

定義域、値域とは？

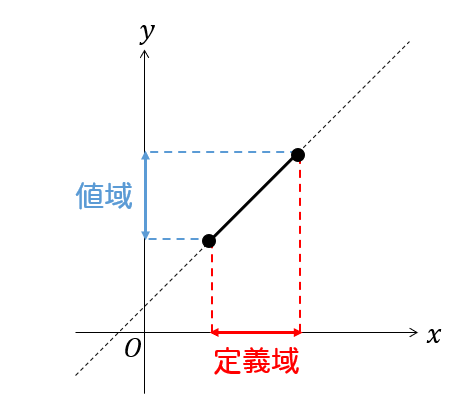
\(x\)のとり得る値の範囲を定義域（ていぎいき）

\(y\)のとり得る値の範囲を値域（ちいき）といいます。

 

言葉が難しく感じるかもしれませんが、

中学で学習してきた言葉を使って説明すると、

定義域とは、\(x\)の変域

値域とは、\(y\)の変域のことをいいます。

定義域が与えられた一次関数のグラフ、値域の求め方

まずは、端点の座標を求めましょう。

端点とは、その名の通り端の点のこと。今回であれば、\(x=-1,2\) の点のことです。

\(x=-1\) を \(y=2x-1\) に代入すると

\(y=2\times (-1)-1=-3\) となるので、\((-1,-3)\)

\(x=2\) を \(y=2x-1\) に代入すると

\(y=2\times 2-1=3\) となるので、\((2,3)\)

 

端点の座標が求まったらグラフに書き込んでいきましょう。

このとき、値域の不等号に注意して、

≦、≧のとき（端点を含む）には、●で座標を書き入れ、

<、>のとき（端点を含まない）には、○で座標を書き入れましょう。

 

座標が書き込めたら、

2点間を実線、それ以外を点線の直線で結んでいきます。

このとき、ついでに\(y\) 軸との交点の座標を書き入れておくのが一般的です。

\(x=0\)を代入したら簡単に求まります。

今回のグラフでは、\(y=2\times 0-1=-1\) となりますね。

 

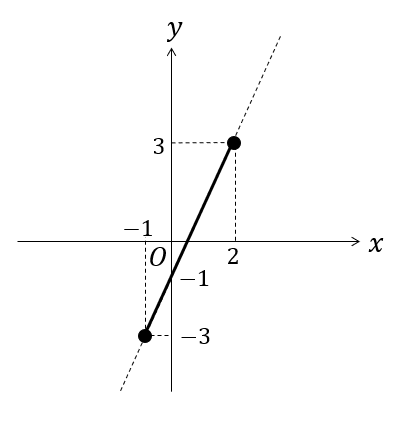
これでグラフは完成！

そして、値域は \(-3≦y≦3\) となります。

 

こちらの問題では、定義域の不等号に注意しましょう。

端点である \(-1\) は「<」となっており、含まれないことになっていますね。

なので、値域を表すときにも \(-1\) のときの\(y\)座標は含まないように表す必要があります。

 

先ほどと同じ手順でグラフをかいていくと、次のようになります。

そして値域は、 \(-5≦y<4\) となります。

\(x=-1\) の点は含まないとなっているので、値域でも\(4\)は含まない。

ということで、不等号を「<」を使うようにしてください。

 

グラフのかき方については、手順を動画でチェックしてもらうと理解が早いですよ＾＾

 

定義域、値域が与えられたときの一次関数の決定

この問題では、\(a\)の符号が明らかになっていないので

グラフの形は次の3パターンが考えられます。

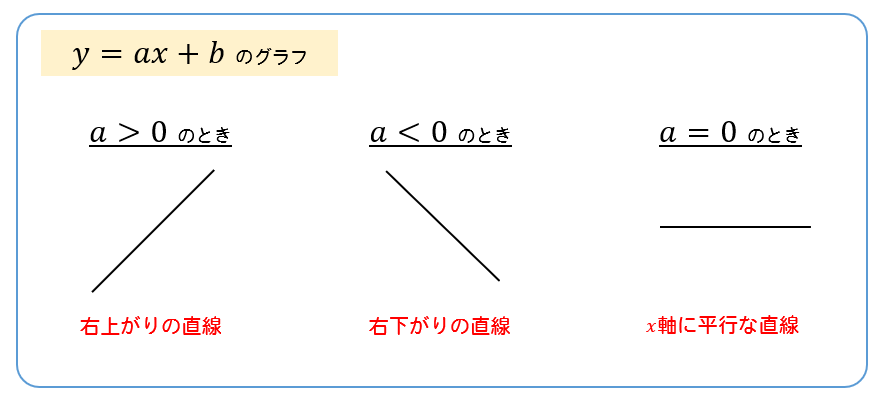
それぞれのパターンに場合分けして、定義域と値域から関数が通る点の座標を見つけていきましょう。

 

まず、\(a=0\) のとき

このときは、\(y=b\) となってしまい、値域を \(1≦y≦7\) とすることは不可能です。

よって、\(a=0\) は不適。

 

次に、\(a>0\) のとき

つまり、右上がりの直線になる場合。

定義域と値域を組み合わせて考えると

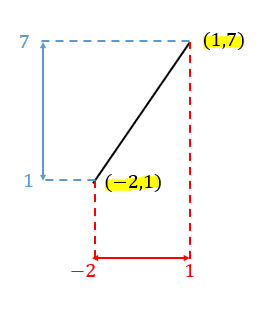
このように2点\((-2,1)\), \((1,7)\) を通ることが分かります。

それぞれの座標を \(y=ax+b\) に代入して、連立方程式を作ります。

$$\begin{eqnarray}
\left\{
\begin{array}{l}
1 = -2a+b \\
7= a+b
\end{array}
\right.
\end{eqnarray} $$

あとは、これを解いていくと

\(a=2, b=5\) と求まります。

このとき、\(a=2\) はちゃんと \(a>0\) を満たしていることも確認しておきましょう。

 

次に、\(a<0\) のとき

つまり、右下がりの直線になる場合。

定義域と値域を組み合わせて考えると

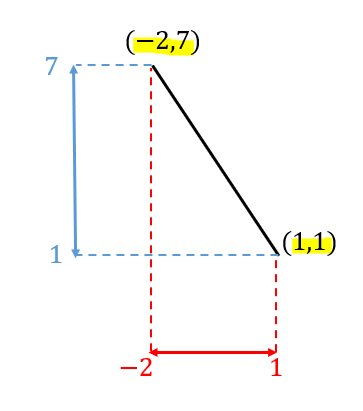
このように2点\((-2,7)\), \((1,1)\) を通ることが分かります。

それぞれの座標を \(y=ax+b\) に代入して、連立方程式を作ります。

$$\begin{eqnarray}
\left\{
\begin{array}{l}
7 = -2a+b \\
1= a+b
\end{array}
\right.
\end{eqnarray} $$

あとは、これを解いていくと

\(a=-2, b=3\) と求まります。

このとき、\(a=-2\) はちゃんと \(a<0\) を満たしていることも確認しておきましょう。

 

以上より

\(a=2, \ b=5\),  \(a=-2, \  b=3\)

となります。

この問題では、先ほどのような場合分けは不要です。

なぜなら定義域、値域の不等号にヒントが隠されているからです。

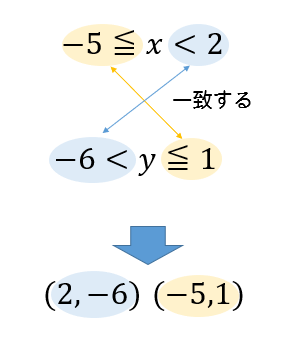
このように、不等号の一致を見つければ関数が通る点の座標を簡単に見つけることができます。

定義域、値域の不等号が異なるときには場合分け不要のラッキー問題となります。

2点\((2,-6)\), \((-5,1)\) を通ることが分かります。

それぞれの座標を \(y=ax+b\) に代入して、連立方程式を作ります。

$$\begin{eqnarray}
\left\{
\begin{array}{l}
-6 = 2a+b \\
1= -5a+b
\end{array}
\right.
\end{eqnarray} $$

あとは、これを解いていくと

\(a=-1, b=-4\) と求まります。

 

まとめ！

お疲れ様でした！

定義域、値域の話は、これから二次関数を含め様々な関数を扱っていく上で、とても重要な内容となります。

何度も記事を読み返し、問題を反復練習して理解を深めておいてくださいね！