今回は中2で学習する「一次関数」の単元から
変域を求める問題について解説していくよ!
変域って…
言葉の響きだけで難しいって思ってる人多いでしょ?
ちゃんと意味を理解していれば
全然難しい問題ではないから
1つ1つ丁寧に学んでいこう!
今回の記事は、こちらの動画でも解説しています(/・ω・)/
一次関数の変域問題
一次関数の変域問題とは、上のようなやつだよね。
記号や符号ばっかりで意味が分かりにくいので
ちょっとかみ砕いて問題を見ていこう。
まず、\(y=2x+1\)という一次関数のグラフがある。
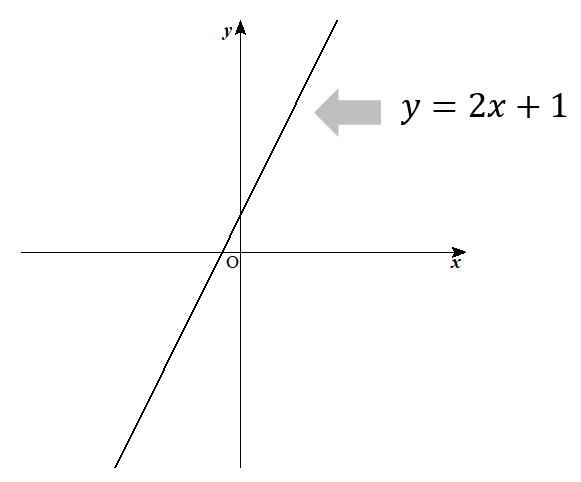
このグラフを\(-1≦x≦3\)の範囲で切り取る。
\(x\)の範囲というのは、グラフでいうところの横の範囲のことだね。
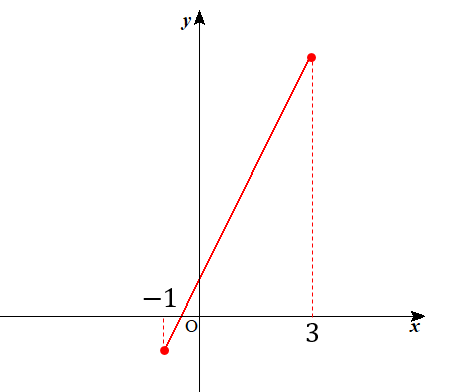
この切り取られたグラフの
縦の範囲を見ていくと、それが\(y\)の変域ということになります。
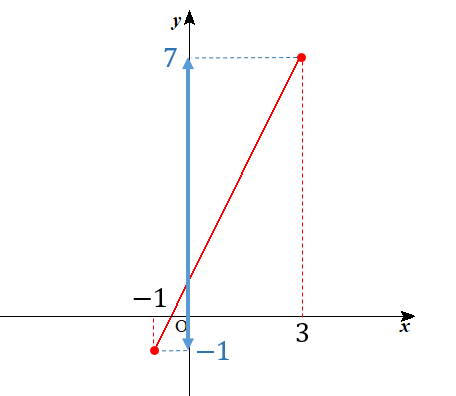
\(x=3\)のときの\(y\)座標は、\(y=2x+1\)に代入して
$$y=2\times 3+1=7$$
\(x=-1\)のときの\(y\)座標は、\(y=2x+1\)に代入して
$$y=2\times (-1)+1=-1$$
グラフから、\(y\)の変域(縦の範囲)は-1から7だということが分かります。
よって、答えは\(-1≦y≦7\)ということになります。
このように、変域の問題というのは
グラフを切り取ったときの横の範囲、縦の範囲について考えているだけなんですね。
ただ、毎回グラフを書いて答えを求めていくのはめんどうだよね。
だから、実際に問題を解くときには
\(x\)の変域である-1と3を式に代入して求めることができる\(y\)座標をそれぞれ見て
(\(y\)座標の小さい方)≦\(y\)≦(\(y\)座標の大きい方)
というように表記してやれば、簡単に答えを求めることができます。
\(y=-3x+2\)について、\(x\)の変域が\(-2≦x≦1\)のとき、\(y\)の変域を求めなさい。
\(x=-2\)のとき
$$y=-3\times (-2)+2=6+2=8$$
\(x=1\)のとき
$$y=-3\times 1+2=-3+2=-1$$
よって、答えは
$$-1≦y≦8$$
ただし、ちゃんとグラフを切り取るイメージは持っておいてね!
じゃないと後で挑戦する応用問題が解けなくなっちゃうからね。
変域の書き方
変域を求める問題は、上で解説したように答えを求めることができます。
だけど、不等号の向きや書き方に疑問を持った方もおられるのではないでしょうか。
実際に、不等号の向きで間違えちゃう人も多いので
不等号の表し方について、ちょっと振り返っておきましょう。
小≦大
不等号はこのように数の大小を表すときに使います。
口が開いている方が大きい方を表していますね。
ここに文字が絡んでくると分かりにくくなっちゃうのですが
ちょっと下の数直線を見てください。
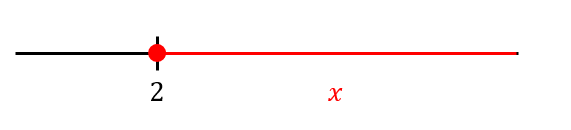
このような\(x\)の範囲を表したいとき
\(x\)は2より右側に位置しているよね。
つまり、\(x\)は2よりも大きい範囲ということです。
だから、不等号で範囲を表すときには
$$\LARGE{2≦x}$$
というように\(x\)の方に口が開いている不等号を使って表します。
\(x≧2\)という表記でもいいけど、なるべく右側に大きい数を持ってきた方がぱっと見で分かりやすいよね。
では、次の数直線を見てください。
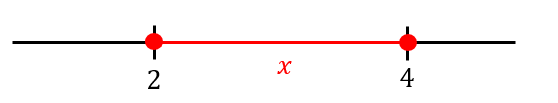
\(x\)は2より右側で、4よりも左側に位置していることが分かります。
つまり
\(2≦x\)であり、\(x≦4\)ということです。
これらをくっつけて表してやると
$$\LARGE{2≦x≦4}$$
このように表すことができます。
\(2≧x≧4\)と表しちゃう人がたまにいますが
これだと、\(x\)は2より小さくて4より大きい!?
という謎の表記になってしまいます。
2より小さくて、4より大きい数ってなーんだ?
なぞなぞの問題みたいですねw
そんなものはありません!

変域から式を求める
それでは、一次関数の変域応用問題に挑戦してみましょう。
このように変域から式を求めるような問題では、グラフをイメージすることが大切です。
傾きが正だから、右上がりのグラフだということがわかります。
そして、横の範囲を4から8で切り取ると
縦の範囲は-3から1になるということなので
グラフのイメージは以下のようになります。
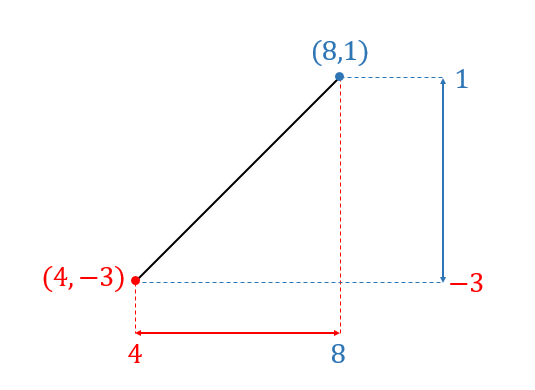
よって、グラフは\((4,-3)\)と\((8,1)\)を通るということが読み取れます。
ここから直線の式を求めていきましょう。
\(y=ax+b\)にそれぞれの座標を代入して
$$-3=4a+b$$
$$1=8a+b$$
これらを連立方程式で解いてやると
\(a=1, b=-7\)となるので
答えは、\(y=x-7\)となります。
変域から式を求めるような問題では
切り取られたグラフをイメージして、座標を読み取りましょう。
座標が分かってしまえば、あとは簡単ですね!
演習問題で理解を深める!
それでは、以上のことを踏まえて理解を深めるために演習問題に挑戦してみましょう!
まとめ
お疲れ様でした!
一次関数の変域問題は、シンプルでしたね
答えを求めることは簡単なのですが
ちゃんと意味が分かっていないと応用問題には挑戦できないので
しっかりと範囲を考えるということがポイントです。
中3生の方は、2乗に比例するグラフの変域についても考えてみましょう。
一次関数の座標の求め方は?いろんな座標を求める問題について解説!
一次関数の増加量に関する問題ってどうやって解く?やり方を解説!
一次関数の変域問題!変域から式を求める方法とは?←今回の記事













わかりやすかったです!
ありがとうございます(^^)
そういっていただけると嬉しいです!
これからも勉強がんばってくださいね
わかりやすい
ありがとうございます!!
よくわかった
お役に立てて良かったです^^
いい復習になりました
ちゃんと復習していて偉いです!
今回の問題が次のテストにでてくるといいな~^^
わかりやすかった
ありがとうございます!
お役に立てて良かったです^^
とても苦戦していたので助かりました!
お役に立てて良かったです!
難しい内容ですががんばってくださいね^^
テストが近っかったため慌ててみましたがわかりやすかったです!
テスト勉強のお役に立てて良かったです^^
変域から式を求める問題でa(変化の割合)が不等号でa<0と指定されている場合どうすればいいでしょうか?
その場合は右下がりのグラフをかいてから
変域を書き込んでみると座標が上手く読み取れますよ^^
すみません。変域から式を求めるという部分のついて、(4,−3)(8,1)から求められる直線の式のy=x+7は誤りであり、y=x−7ではありませんか?
ご指摘ありがとうございます!!
訂正しておきました!