【苦手な人向け】絶対値のついたグラフを書いてみよう！

今回の記事では、数学が苦手な人に向けて

「絶対値のついたグラフの書き方」

をイチから順に解説していきます。

 

今回の記事を通してマスターしたいのは次の2つだ！

 

こちらの動画も参考にしてください＾＾

絶対値のついたグラフの書き方（直線）

絶対値のついたグラフは、

• 中身が0以上になるとき ⇒ 中身がそのまま
• 負になるとき ⇒ 中身にマイナスをつける

で場合分けをして絶対値をはずすのがポイントです。

 

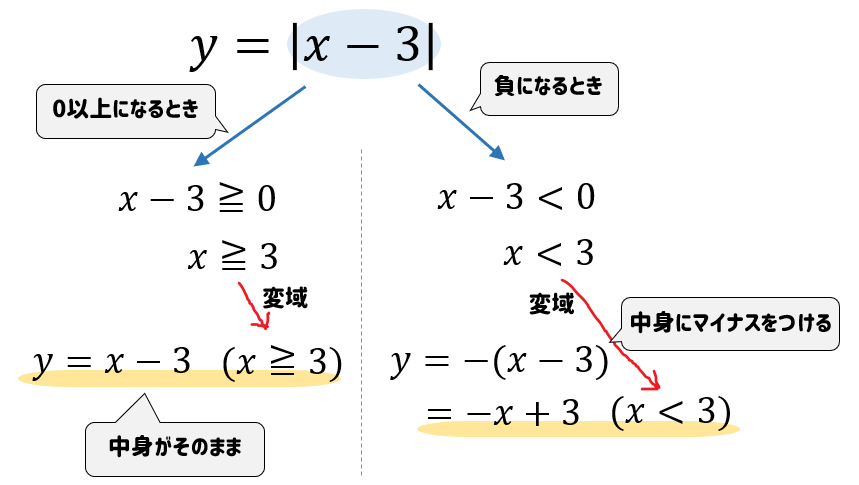
すると、このように絶対値がはずれた式が2つできあがります。

これらを変域のところで切り取ってグラフを書いていきましょう。

それぞれ一次関数のグラフです。書き方を忘れた方はこちらの記事で復習しておいてください。

⇒ 一次関数のグラフの書き方を解説！

 

まずは、\(y=x-3(x≧3)\)を書いてみましょう。

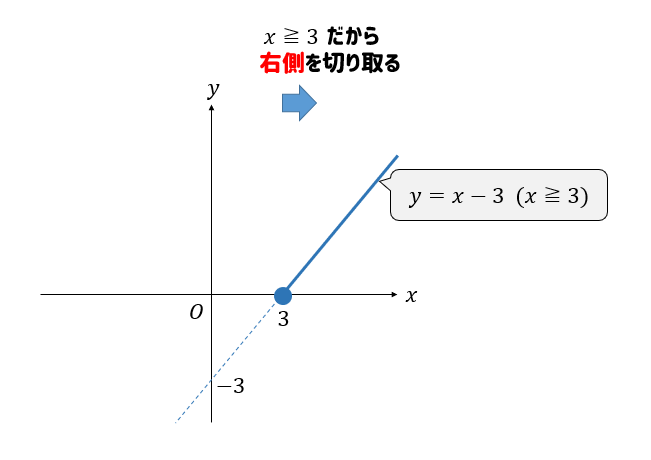
変域が\(x≧3\)ということから、3よりも右側の部分が残るように切り取りましょう（実線部分）

 

次に、\(y=-x+3(x<3)\)を書いてみましょう。

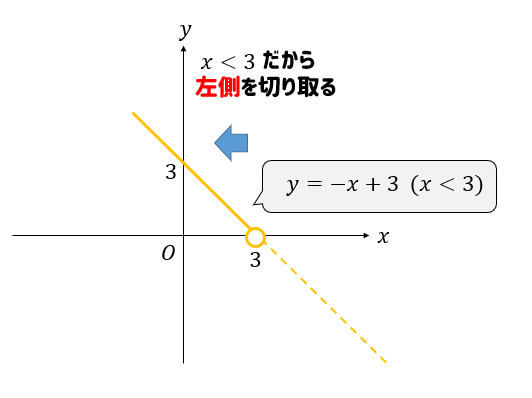
変域が\(x<3\)ということから、3よりも左側の部分が残るように切り取りましょう（実線部分）

 

この2つのグラフを1つにまとめると次のようになります。

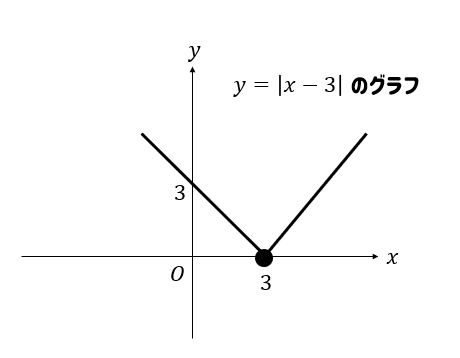
これで絶対値のグラフ完成です！

手順としては次の通り

 

ちなみに、式全体に絶対値がついているグラフというのは

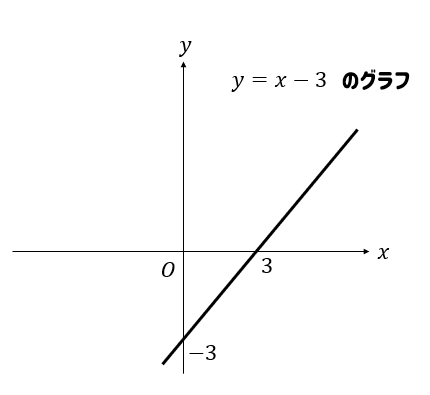
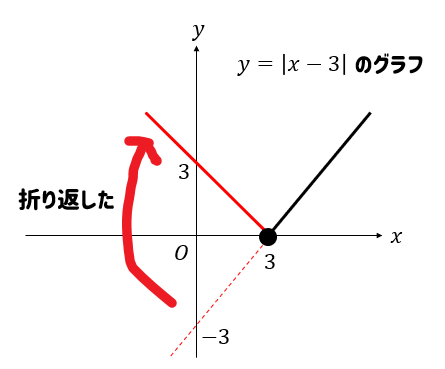
このように、絶対値をそのままはずした場合のグラフを\(x\)軸の部分で折り返された形。

と覚えておいてもOKです。

絶対値のついたグラフの書き方（放物線）

絶対値の中身が二次関数になっていますが、手順としては同じです。

まずは絶対値の中身が0以上、負になる場合で場合分けをしましょう。

※中身が二次関数の場合、場合分けには二次不等式の知識が必要となります。

⇒ 二次不等式の解き方を簡単に！高校数学をマスターしよう！

【中身が0以上になる場合】

$$\begin{eqnarray}x^2-2x-3&≧&0\\[5pt](x-3)(x+1)&≧&0\\[5pt]x≦-1,3&≦&x \end{eqnarray}$$

このとき、絶対値はそのままはずすことができるので

$$y=x^2-2x-3(x≦-1,3≦x )$$

となります。

【中身が負になる場合】

$$\begin{eqnarray}x^2-2x-3&<&0\\[5pt](x-3)(x+1)&<&0\\[5pt]-1<x&<&3 \end{eqnarray}$$

このとき、絶対値はマイナスをつけてはずすので

$$\begin{eqnarray}y&=&-(x^2-2x-3)\\[5pt]&=&-x^2+2x+3(-1<x<3) \end{eqnarray}$$

となります。

 

それぞれ場合分けをして2つの式が作れたら、ここからグラフ下記の作業に入っていきましょう。

また、二次関数のグラフを書くためには平方完成で頂点を求める必要があります。

その辺の手順を忘れてしまった場合はこちらの記事をご参考ください。

⇒二次関数グラフの書き方を初めから解説！

 

まずは、\(y=x^2-2x-3(x≦-1,3≦x)\)のグラフを書いてみましょう。

平方完成して頂点を求めると

$$\begin{eqnarray}y&=&x^2-2x-3\\[5pt]&=&(x-1)^2-1^2-3\\[5pt]&=&(x-1)^2-4 \end{eqnarray}$$

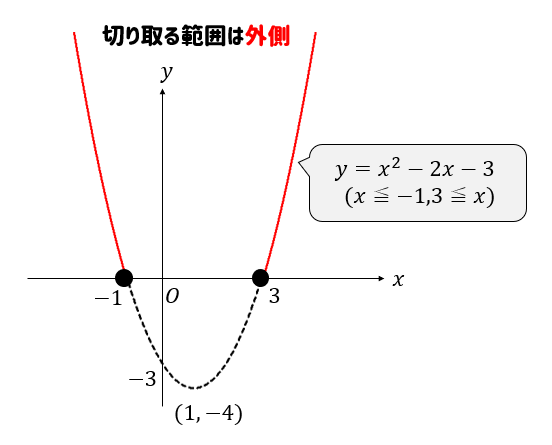
変域が\((x≦-1,3≦x)\)ということから、\(-1,3\)よりも外側の部分が残るように切り取りましょう（実線部分）

 

次は、\(y=-x^2+2x+3(-1<x<3)\)のグラフを書いてみましょう。

平方完成して頂点を求めると

$$\begin{eqnarray}y&=&-x^2+2x+3\\[5pt]&=&-(x^2-2x)+3\\[5pt]&=&-\{(x-1)^2-1\}+3\\[5pt]&=&-(x-1)^2+4 \end{eqnarray}$$

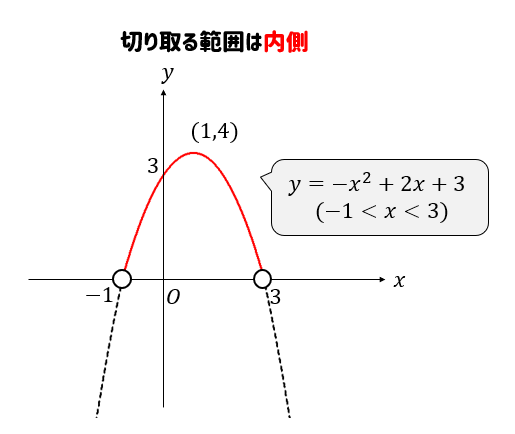
変域が\((-1<x<3)\)ということから、\(-1,3\)の内側の部分が残るように切り取りましょう（実線部分）

 

この2つのグラフを1つにまとめると次のようになります。

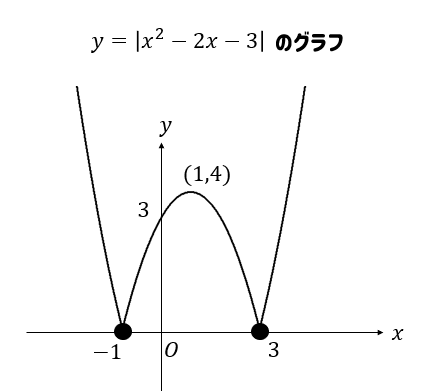
これで絶対値のグラフ完成です！

 

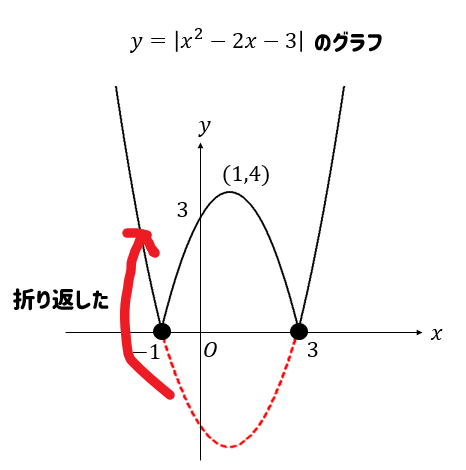
こちらのグラフも\(y=x^2-2x-3\)のグラフを\(x\)軸で折り返したと考えてもOKですね。

まとめ！

絶対値のグラフの書き方についてまとめておきましょう。

 

とにかく、丁寧に場合分けをすることが大事です。

いや、場合分けをしなくても\(x\)軸で折り返せばいいんでしょ？と考えていると甘いです。

$$y=|x-1|+5$$

のように絶対値の外にも式があるときには、単純に折り返すというわけにはいきません。

しっかりと場合分けをする必要が出てくるのです。

 

というわけで、今回の記事を何度も見直して、場合分けをしながら絶対値のグラフが書けるように練習しておきましょう。

ファイトだぞ(/・ω・)/