こんにちは!数スタの小田です。
今回は中2で学習する『一次関数』の中から
直線のグラフの書き方について解説していきます。
グラフを書くための、ちょっとしたコツがあります。
そのコツを学んでもらえたら
グラフなんてちょちょいのちょいです!

傾き、切片が分数になっているような
応用問題も解説していくので
この記事を通して、一次関数のグラフをマスターしていきましょう!

グラフを書くために知っておくこと
まずは、一次関数のグラフを書くために
知っておくべきことがあります。

xに掛けられている数を傾き
文字がついていない数だけのものを切片(せっぺん)といいます。
傾きというのは
直線がどれくらいの増え方をするかを表しています。
傾きを分数にして
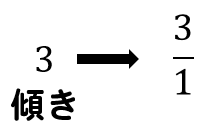
分母の数だけ右へ
分子の数が+なら上へ、-なら下へ
数の分だけ変化していきます。

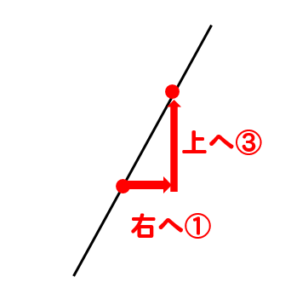
切片というのは
直線がy軸のどこで交わるかを表しています。
切片が1というのは
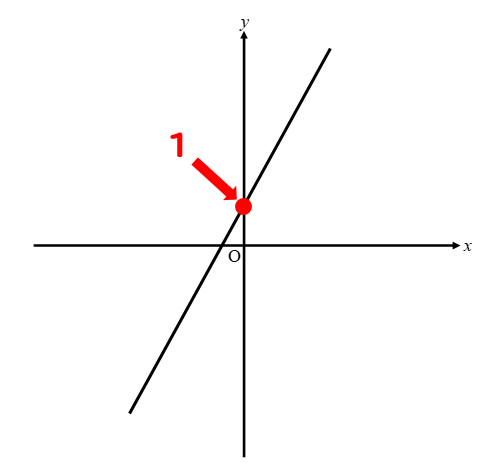
このようにy軸と1の部分で交わることを表しています。
まずは、グラフを書くための予備知識として
傾き、切片というものを覚えておいてください。
グラフの書き方手順
それでは、上で紹介した予備知識をもとに
グラフの書き方の手順を紹介します。
- 傾き、切片を読み取る
- 切片の点を取る
- 傾き分だけ動かしたところに点を取る
- 2点を線で結ぶ
この4つの手順通りやっていけば
グラフは簡単に書けるようになります(^^)
それでは、例題を通して
この手順の確認をしていきましょう。
例題
次の一次関数のグラフをかきなさい。
$$y=2x+3$$
手順① 傾き、切片を読み取る
まずは式から、傾きと切片を読み取ります。
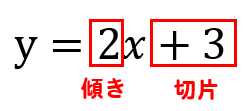
傾き⇒2
切片⇒3 が式から読み取れますね。
手順② 切片の点を取る
次は、切片から点をy軸に取ります。
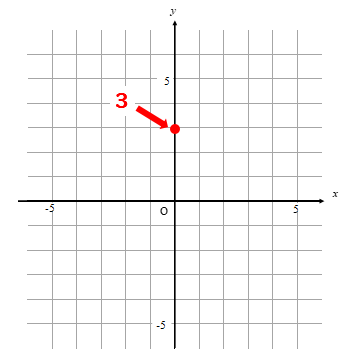
切片は3なので
y軸の3の部分に点を取ります。
手順③ 傾きの分だけ動かしたところに点を取る
傾きはグラフの増え方を表している数でしたね。
傾きを分数にしてやって、どれだけ変化していくのかを見ます。


分母の数だけ右へ
分子の数だけ上下へ動くことを表しているので
傾き2 ⇒ 右へ1、上へ2動いていきます。
先ほど点をとった切片の部分から右へ1、上へ2動かしたところに点を取りましょう。
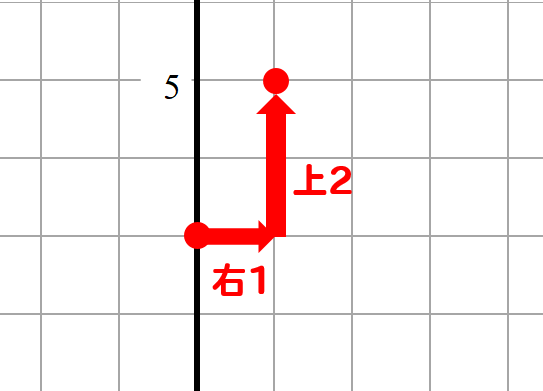
手順④ 2点を線で結ぶ
最後に、2点を線で結べば
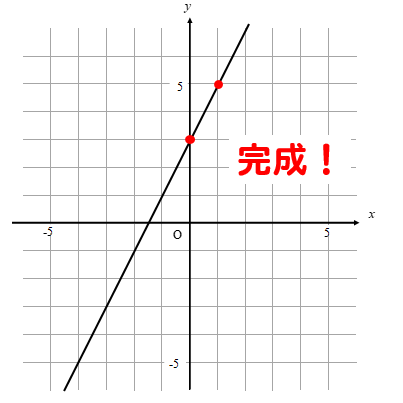
グラフの完成です!
手順③の傾き部分だけ
慣れるまで練習が必要かもしれませんが
1つ1つの手順は、難しいものではありませんね(^^)
それでは、いくつかの練習問題を通して
理解を深めていきましょう。
練習問題で理解を深める!
次の一次関数のグラフを書きなさい。
$$(1)y=-x+2$$
$$(2)y=\frac{2}{3}x-1$$
$$(3)y=-\frac{3}{4}x+5$$
問題(1)の解説!
$$(1)y=-x+2$$
手順① 傾き、切片を読み取る
傾き ⇒ -1
切片 ⇒ 2
手順② 切片の点を取る
切片2なので、y軸の2の部分に点を取ります。
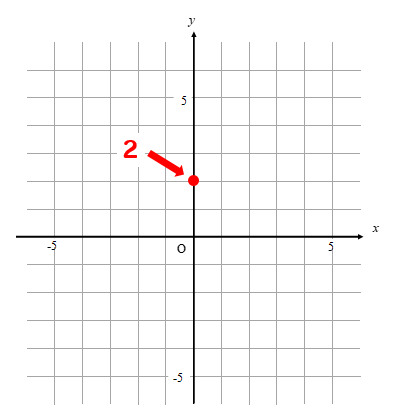
手順③ 傾きの分だけ動かしたところに点を取る
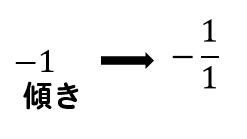
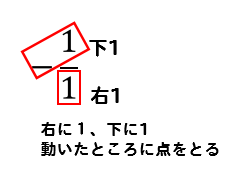
傾き-1を分数に表して
分母の数1だけ右に動いて
分子の数-1だけ下に動かします。
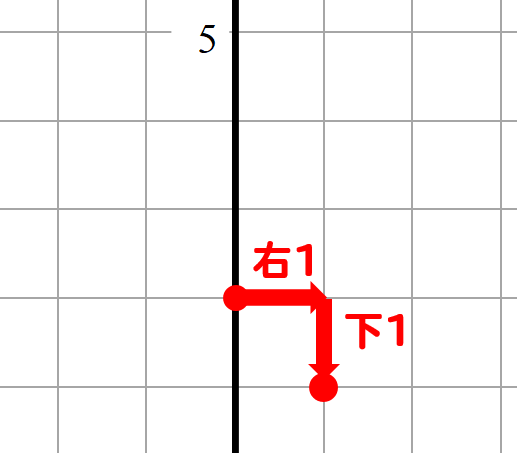
手順④ 2点を線で結ぶ
最後に2点を線で結べば完成です!
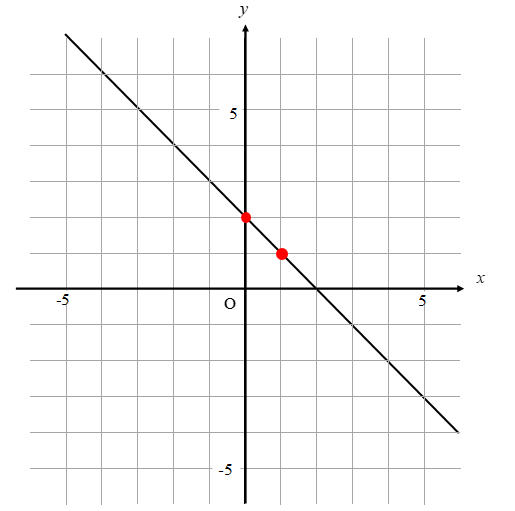
傾きがマイナスのときは
右に下がっていくようなグラフになりますね。
問題(2)の解説!
$$(2)y=\frac{2}{3}x-1$$
手順① 傾き、切片を読み取る
傾き ⇒ \(\frac{2}{3}\)
切片 ⇒ -1
手順② 切片の点を取る
切片-1なので、y軸の-1の部分に点を取ります。

手順③ 傾きの分だけ動かしたところに点を取る

傾きが最初から分数なので
分数に変換する手間が省けますね。
傾きが分数の方が、ちょっとラク♪
分母の数3だけ右に動いて
分子の数2だけ上に動かします。

手順④ 2点を線で結ぶ
最後に2点を線で結べば完成です!

傾きが分数だと、ちょっとラクでしたね♪
問題(3)の解説!
$$(3)y=-\frac{3}{4}x+5$$
手順① 傾き、切片を読み取る
傾き ⇒ \(-\frac{3}{4}\)
切片 ⇒ 5
手順② 切片の点を取る
切片5なので、y軸の5の部分に点を取ります。
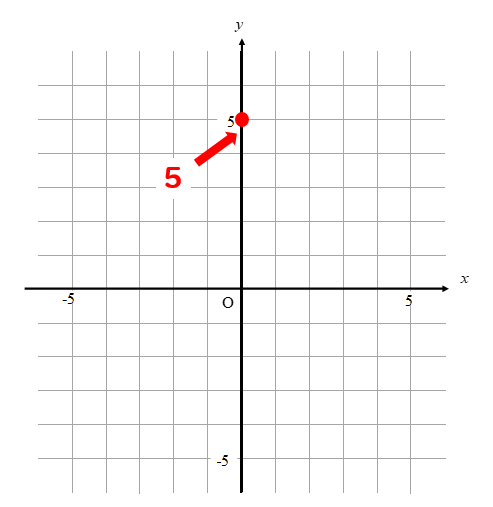
手順③ 傾きの分だけ動かしたところに点を取る
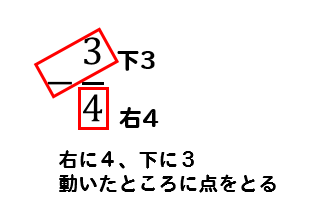
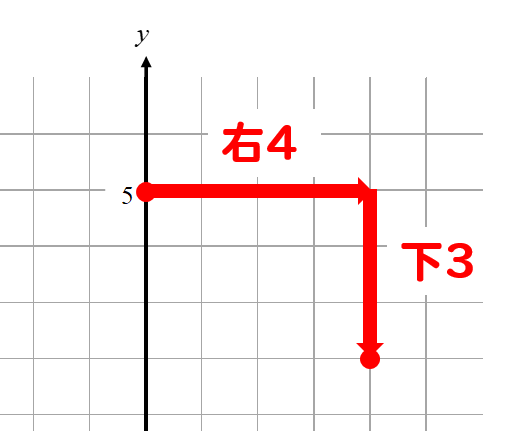
分母の数4だけ右に動いて
分子の数-3だけ下に動かします。
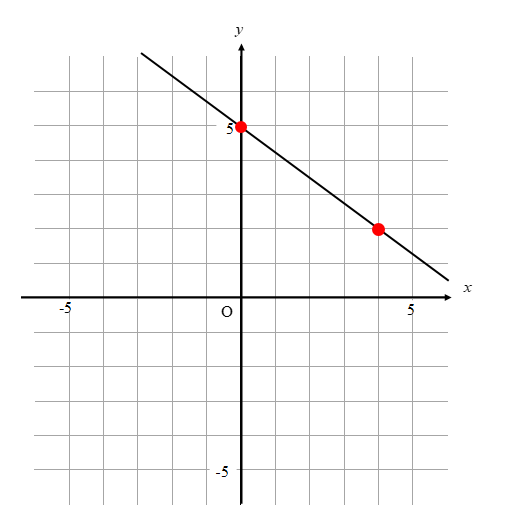
手順④ 2点を線で結ぶ
最後に2点を線で結べば完成です!
これらの例題3問が理解できれば
だいたいのグラフは書けるはずです!
最後に、切片が分数になっている応用編も解説しておきます。

【応用】切片が分数になっているグラフの書き方
次の一次関数のグラフを書きなさい。
$$y=\frac{2}{3}x-\frac{1}{3}$$
切片が分数になっている場合
今まで紹介した手順でグラフを書こうとすると
困ったことが起こります。

切片の点が取れない!?
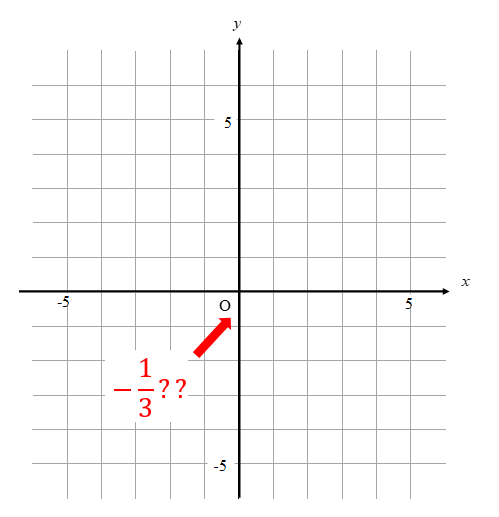
切片が分数なので、正確な点を取ることができません。
このような場合にはどうすればよいか…
x、yともに整数になる点を見つける!
表を書いて、ともに整数になるところを見つけます。
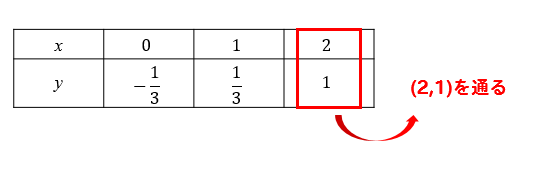
整数になるところが見つかれば、点を取ります。

点が取れたら
この点を基準に傾きの分だけ動かしていきます。

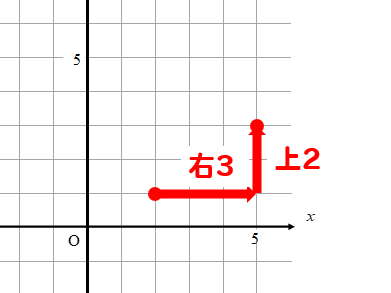
最後に2点を結んでやれば完成です。
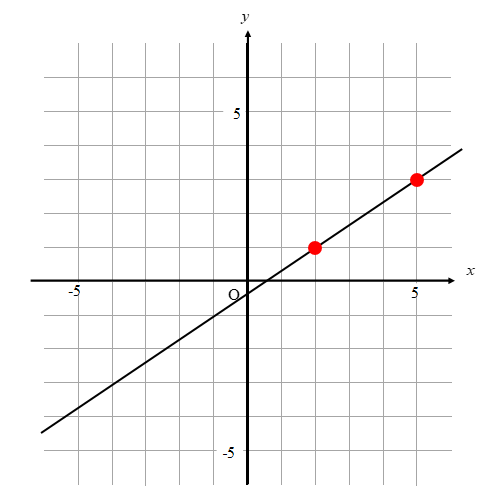
切片が分数になっている場合には
表を作り、ともに整数になるところを見つけて点を取ります。
点が取れたら、そこから傾き分だけ動かして
2点を結んでやれば完成です!
【演習プリント】手を動かしてグラフの書き方を完全習得だ!
お疲れ様でした!
ここまでのところでグラフの書き方は一通り理解してもらえましたか?
記事を読んでいると
「ふむふむ、なるほど~」
と納得できた気持ちになるのですが、
実際にグラフに書いてみようとすると…
「なにからやればいいんだっけ~!!」
と、困ってしまうことがあります(^^;)
なので、理解したつもりを防ぐためにも
実際に手を動かしてグラフを書いてみて欲しいです!
というわけで!
こちらのプリントでグラフを書いてみましょう(‘ω’)ノ
動画による解説もつけておいたので、
数学が苦手な方でも安心して最後までやり切ることができますよ^^
プリントを使ってグラフの書き方を完璧に仕上げておきたい!
という方には、こちらから詳しい解説動画&プリントをお渡ししています。
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れます^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
答えが合っているかどうかだけでなく、動画解説を活用して『書き方の手順』『解法のポイント』といったところもチェックしておいてくださいね^^
解答を受け取ってくれた方には、引き続きいろんな問題をメールでお届けする予定なのでお楽しみに^^
一次関数のグラフの書き方 まとめ
それでは、最後にグラフの書き方をおさらいしておきましょう。
グラフの書き方の手順は以下の通りでしたね。
- 傾きと切片を読み取る
- 切片から点を取る
- 傾きの分だけ動いたところに点を取る
- 2点を結ぶ
傾きは、分数の形にしてやると


グラフがどのように増えていくのかを読み取ることができました。
グラフの応用編として
切片が分数になっているようなものがあります。
$$y=\frac{2}{3}x-\frac{1}{3}$$
このような場合には、切片の点が取れないので
x、yともに整数となる点を表を書きながら見つけていきます。

点が見つかれば、そこから傾き分だけ動かして線で結べば完成です。


一次関数のグラフの書き方いかがでしたでしょうか?
この手順をしっかりと覚えておけば
ちょちょいのちょい~♪

で解けてしまうくらい簡単な問題なので
しっかりと練習して身につけておきましょう!














とても分かりやすかったです
ありがとうございました!!
嬉しいコメントありがとうございます(^^)
これからも勉強頑張っていこう!
自習で勉強してて、傾きが分数の時のグラフの書き方がどこ見てもなくて、わからなかったところ、このページを見つけて、めちゃくちゃわかりやすくて、スカッとしました。笑
本当にありがとうございました!!
それは良かった!
記事を一生懸命に書いた甲斐があります(^^)
困ったことがあれば、是非とも数スタをご参考ください(/・ω・)/
コメントありがとう!
分かりやすかった!ありがとうございます!
理解してもらえて嬉しいです!
ありがとうございます(^^)
xと切片が分数の問題でずっと止まってました…でもこのブログで解き方を学んでからはスラスラ解けるようになりました!ありがとうございます!
切片が分数になっているとちょっと難しいもんね(^^;)
でも、スラスラ解けるようになったようで素晴らしいです!
こちらこそコメントありがとうございました!
めっちゃわかりやすいです
それは良かった!
嬉しいコメントありがとう(^^)
出来なくて出来なくてとても迷ってたのにこんなに簡単に解けるなんて凄すぎる!
分かりやすくて簡単なやり方ありがとうございました
こらからも活用したいと思います!!
ありがとうございます!
どんどん活用してください(/・ω・)/
切片が分数のところが全く分からなかったので助かります
m(_ _)m
分数だとややこしいもんね(^^;)
お役に立てて良かったです!
雇いたいです
雇ってくださいぃぃぃ!!!
分かりやすくて分かりやすかったです!
ありがとうございます^^
他のサイトみても全然わからなかったけど一瞬で理解することができました!ありがとうございます