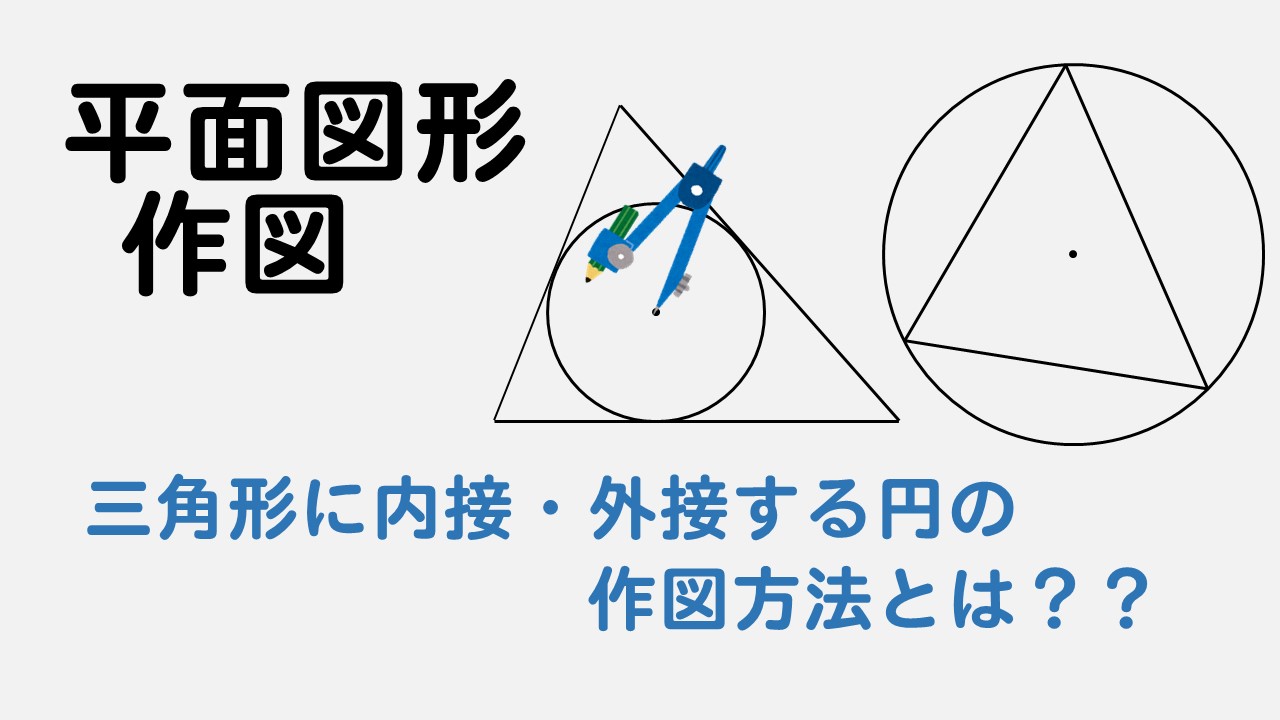
今回は中1で学習する作図の単元から
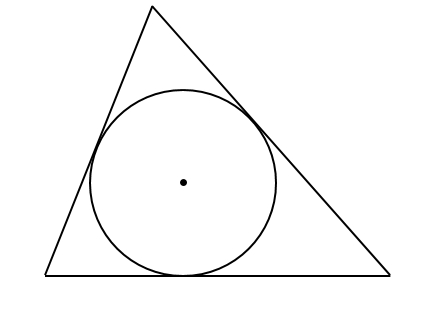
三角形の内側にピタッとくっついている内接円のかき方
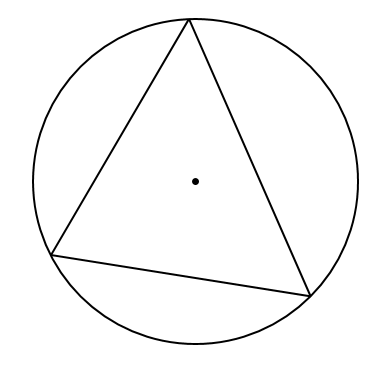
三角形の外側にピタッとくっついている外接円のかき方
について解説していきます。
この内接円、外接円というのは
高校生になると取り扱う機会が多くなります。
キレイな内接円、外接円をかくことができるようになると
問題も解きやすくなるからね!
今回の記事を通して、それぞれの作図方法をしっかりと学んでいきましょう。
内接円とは
内接円というのは、図形の内側にピタッとはまっている円のことをいいます。
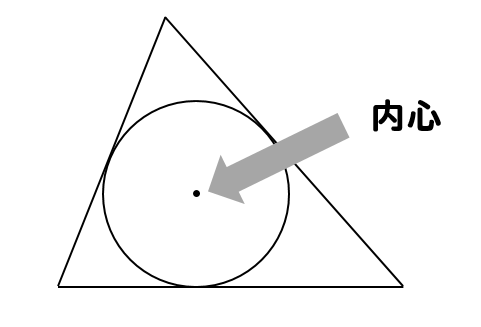
ちなみに、内接円の中心のことを内心といいます。
この用語は、高校生の方だけしっかりと覚えておいてください。
円がピタッとはまっているということは
それぞれの辺が、円の接線になっているということを表しています。
よって、円の中心からそれぞれの接点に線をひくと
それらの線は、円の半径になっていて
すべて長さが等しいということになります。
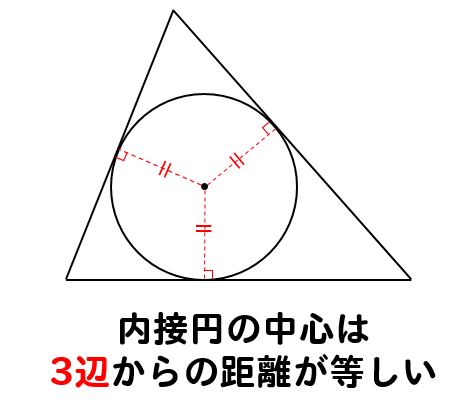
つまり
内接円の中心は、3辺からの距離が等しい点にあるということがわかります。
角の二等分線を利用すれば
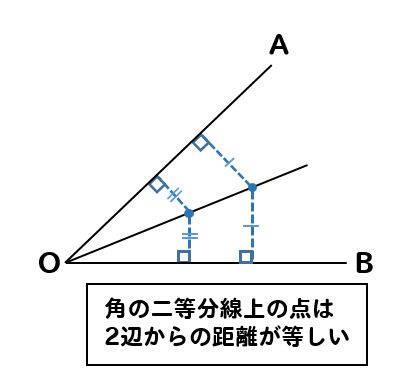
各辺からの距離が等しい点を作図することができましたね。
これを利用して内接円の中心を求めて作図をしていきます。
内接円の作図、書き方とは
それでは、次の三角形に内接する円を作図していきましょう。
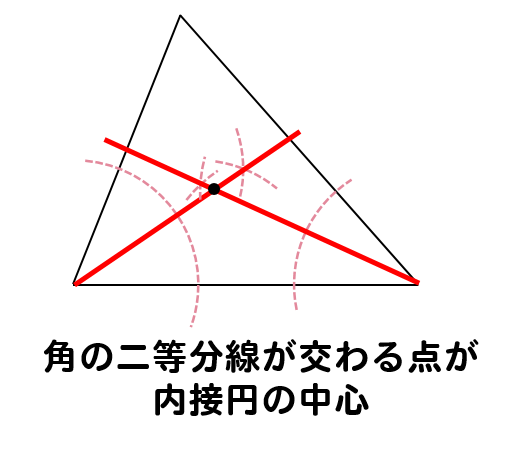
内接円の中心を求めるために
角の二等分線をひいて、それぞれの交わる点を見つけます。
内接円の中心が分かったら
次は半径の大きさを調べます。
中心から、三角形の辺に向かって垂線をひきます。
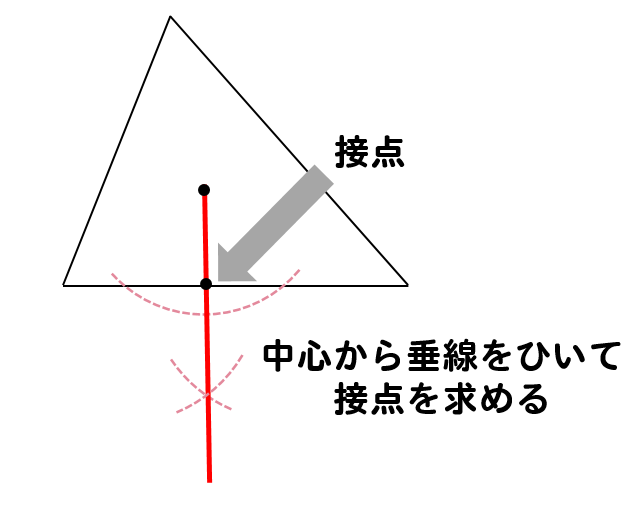
すると、接点の場所がわかるので
中心と接点の長さを半径として円をかきます。
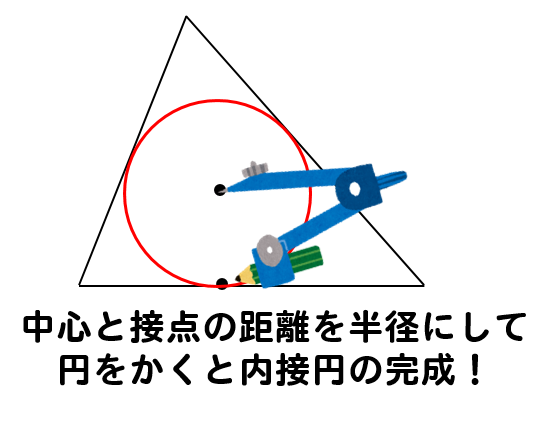
これで内接円の完成です!
内接円の作図手順
- 角の二等分線をかいて、内接円の中心を作図する
- 中心から垂線をひいて、接点を作図する
- 中心と接点から半径を求めて、円をかく

内接円の性質とは
上の作図から分かる通り
内接円の中心は、角の二等分線上にあります。
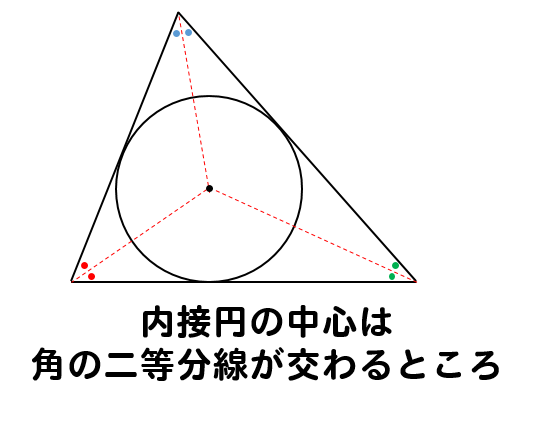
内接円に関しては、作図だけでなく角度を求める問題も出題されるので
この性質をちゃんと覚えておく必要があります。
外接円とは
外接円とは、図形の外側にピタッとくっついている円のことですね。

外接円の中心のことを外心というので
高校生の方は、しっかりと覚えておきましょう。
図形の角頂点と、外接円の中心を線で結ぶと
それぞれの線は、外接円の半径になっているので
長さがすべて等しくなります。
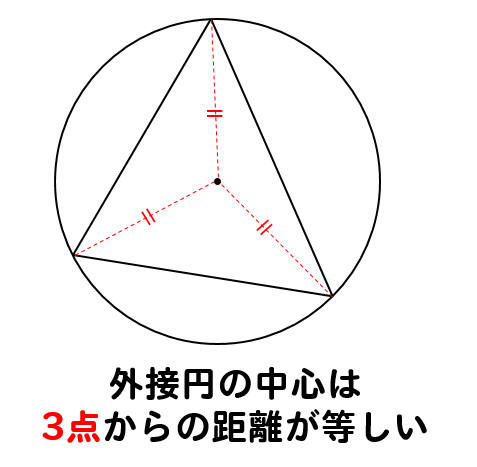
つまり
外接円の中心は、図形の各頂点から距離が等しいところにあることがわかります。
2点から等しい距離にある点を作図したい場合には
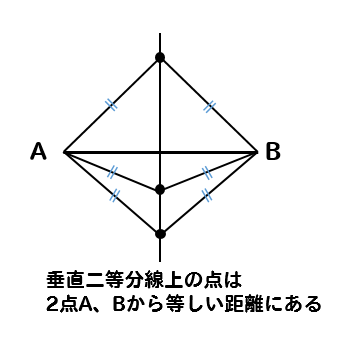
垂直二等分線を利用すれば良かったですね。
これを使って、外接円の中心を求めて作図を進めていきましょう。
外接円の作図、書き方とは
次の三角形に外接する円を作図していきましょう。
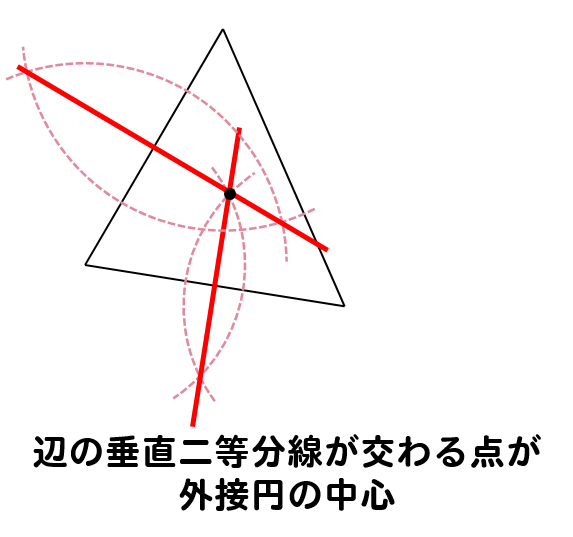
外接円の中心は、各点からの距離が等しいところになるので
各辺の垂直二等分線を作図して、中心を求めます。
中心が求まったら
中心から各頂点への距離を半径として円をかきます。
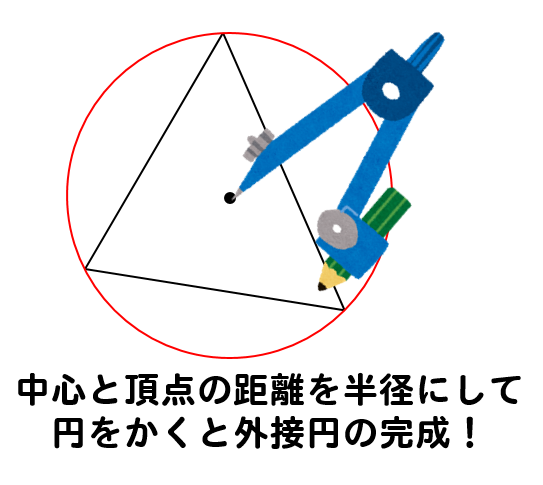
これで外接円の完成です!
外接円の作図手順
- 各辺の垂直二等分線をかいて、外接円の中心を作図する
- 中心と各頂点から半径をとって、円をかく
外接円の性質
それでは、作図を通してわかった外接円の性質をまとめおきましょう。
まず、外接円の中心は各辺の垂直二等分線上にあるということがわかりましたね。
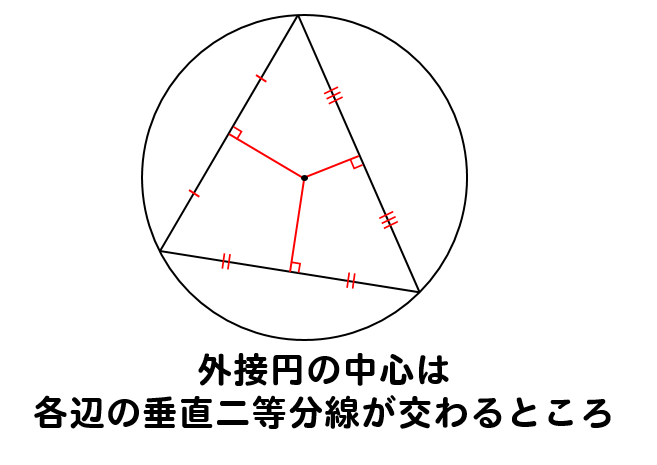
この性質は、作図以外の問題で利用することがほとんどありません。
作図するときにご活用ください。
他には、三角形の外接円を考える場合には
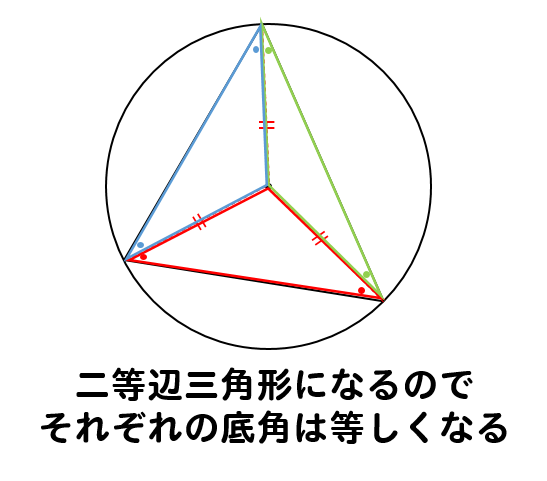
このように、二等辺三角形を3つ作ることができるので
それぞれの底角は同じ大きさになります。
この性質は、角度を求めさせるような問題でよく出題されるので覚えておきましょう。
まとめ
お疲れ様でした!
内接円は角の二等分線
外接円は垂直二等分線
を利用することで作図できました。
また、それぞれの性質のところでまとめたように
どこの角が等しくなるか
という性質は、問題に出題されやすいのでしっかりと覚えておきましょう。


円や角度に関する作図はこちらもご参考ください(^^)
角度15°・30°・45°・60°・75°・90°・105°の作り方とは?















かけたよ
期末もばっちりだね
やったね!!
この調子で期末も頑張ろう(^^)
すごい分かりやすかったです!簡潔にかかれていたし、スペースがあって読みやすかったです!他の単元などもあって違うページにとべてとてもいいです!これで学長も行けるはず!ありがとうございます!♡♡
嬉しいコメントありがとうございます!
勉強がんばってくださいね(/・ω・)/
(๑•̀ㅂ•́)و✧できたぁー
さすがです!!(‘ω’)ノ
やったー