今回は中１で学習する空間図形の単元から
円柱の体積、表面積の求め方を徹底解説していくよ！
この記事を通して
円柱の問題はバッチリ！な状態になってもらうから
がんばっていこう！
Contents
円柱の表面積を求める方法
この円柱を使って解説を行っていきます。
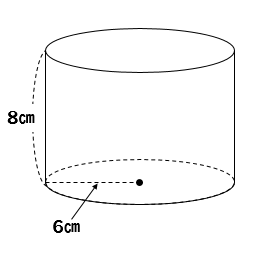
円柱の表面積を求めるためには
底面積と側面積を求めて合計する必要があります。
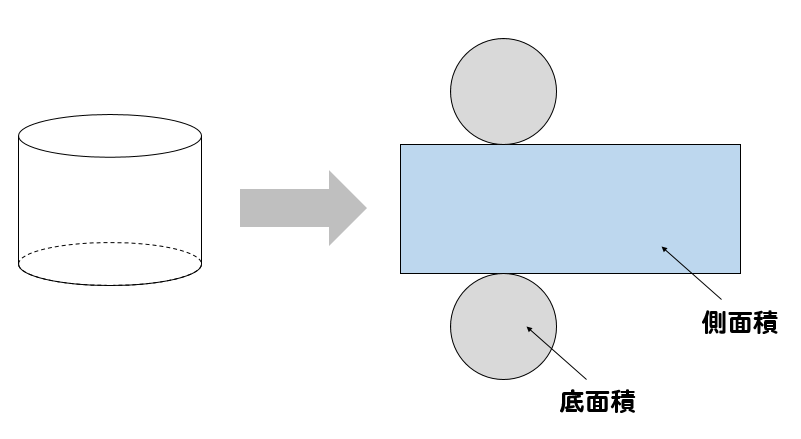
それでは、底面積と側面積をそれぞれ求めてみましょう。
円柱の底面積の求め方
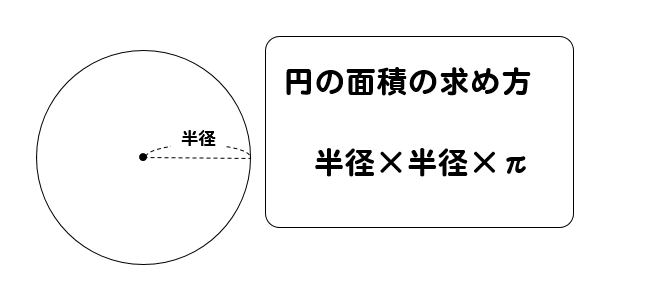
円柱の底面は円の形をしています。
ということで、円の面積の求め方を覚えておけばバッチリです！
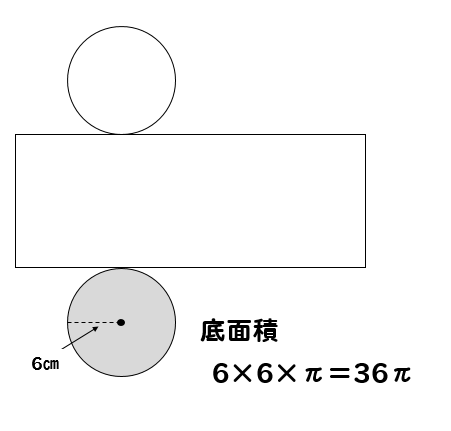
底面の半径は6㎝なので
底面積は
$$6\times 6\times \pi=36\pi (cm^2)$$
となります。
円柱の側面積の求め方
円柱の側面積は長方形の形をしています。
円柱の高さが、側面の縦の長さ
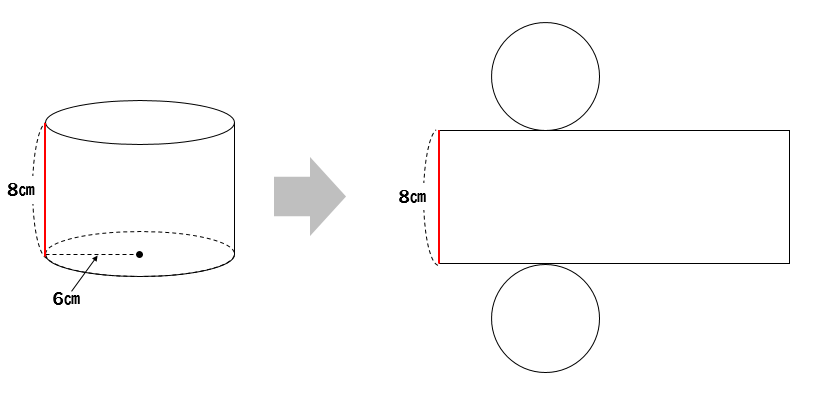
底面の円周の長さが、側面の横の長さ
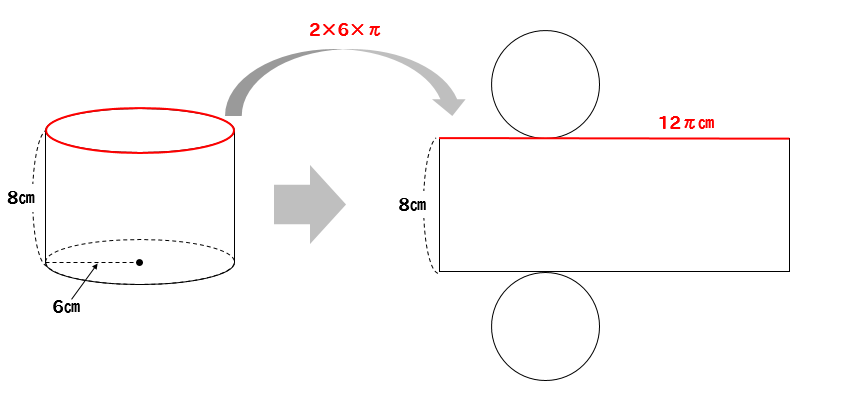
にそれぞれ対応しています。
円周の長さの求め方も覚えておきましょう！
側面積の縦と横の長さがそれぞれ求まったら計算していきましょう。
長方形の面積は（縦）×（横）でしたね。
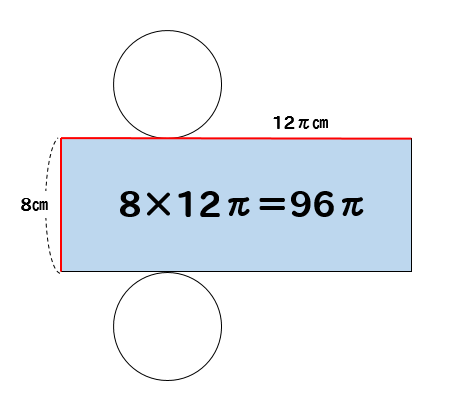
よって、側面積は
$$8\times 12\pi =96\pi (cm^2)$$
となります。
円柱の表面積を求める
底面積と側面積がそれぞれ求まったら
それらを合計することで表面積を求めることができます。
よって、円柱の表面積は\(168\pi (cm^2)\)となります。
円柱の表面積を求める公式$$(底面積)\times 2+(側面積)$$
円柱の体積を求める方法
円柱の体積を求める方法は
とーーーーっても簡単です。
底面積×高さ
これだけ！
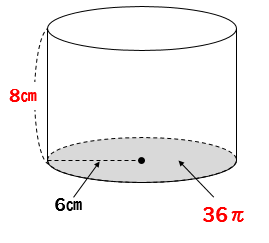
底面積は\(36\pi (cm^2)\)
高さは\(8cm\)なので
円柱の体積は
$$36\pi \times 8=288\pi (cm^3)$$
となります。
$$(底面積)\times (高さ)$$
練習問題で理解を深める！
次の立体の体積、表面積をそれぞれ求めなさい。
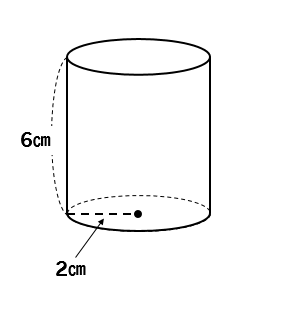
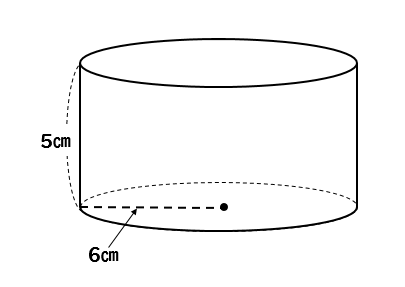
まとめ
お疲れ様でした！
最後にもう一度、円柱の公式を確認しておきましょう。
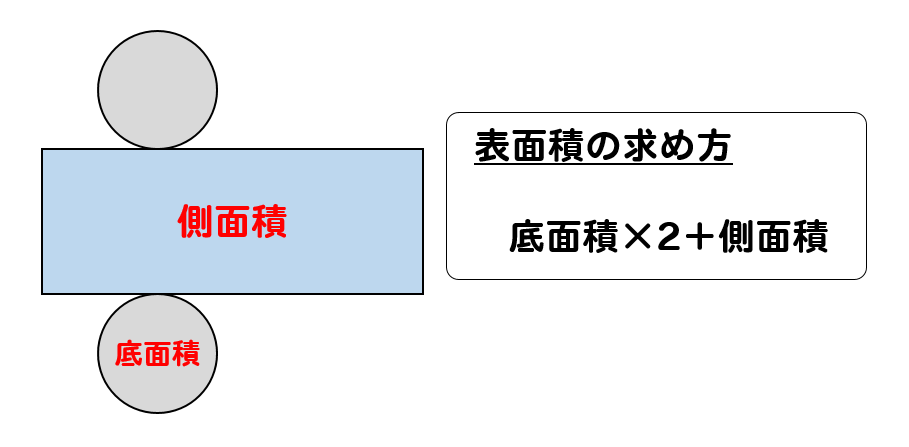
円柱の表面積、体積の求め方はこれでバッチリですね。
あとは学校のワークなどを通して
たくさん問題演習を繰り返して理解を深めていきましょう！
ファイトだー(/・ω・)/
効率よく学習を進めていきたい方は必見！
この記事を通して、学習していただいた方の中にはもっといろんな単元の学習を進めていきたい！
という素晴らしい学習意欲を持っておられる方もいる事でしょう。
だけど
どこの単元を学習すればよいのだろうか。
何を使って学習すればよいのだろうか。
勉強を頑張りたいけど 何をしたらよいか悩んでしまって
手が止まってしまう…
そんなお悩みをお持ちの方もおられるのではないでしょうか。
そんなあなたには
スタディサプリを使うことをおススメします。
スタディサプリを使うことで
どの単元を学習すればよいのか 何を解けばよいのか
そういった悩みを全て解決することができます。
スタディサプリでは学習レベルに合わせて授業を進めることが出来るほか、たくさんの問題演習も行えるようになっています。
スタディサプリが提供するカリキュラム通りに学習を進めていくことで
何をしたらよいのか分からない…
といったムダな悩みに時間を割くことなく
ひたすら学習に打ち込むことができるようになります(^^)
また、スタディサプリにはこのようなたくさんのメリットがあります。
- 費用が安い！月額1980円で全教科全講義が見放題です。
- 基礎から応用まで各レベルに合わせた講義が受けれる
- 教科書に対応！それぞれの教科に沿って学習を進めることができる
- いつでもどこでも受講できる。時間や場所を選ばず受講できます。
- プロ講師の授業はていねいで分かりやすい！
- 都道府県別の受験対策もバッチリ！
- 合わないと感じれば、すぐに解約できる。
今までの悩みを解決し、効率よく学習を進めていきましょう。
「最近、成績が上がってきてるけど塾でも通い始めたの？」
「どんなテキスト使ってるのか教えて！」
「勉強教えてーー！！」
スタディサプリを活用することで どんどん成績が上がり
友達から羨ましがられることでしょう(^^)
今まで通りの学習方法に不満のない方は、スタディサプリを使わなくても良いのですが
学習の成果を高めて、効率よく成績を上げていきたい方
是非、スタディサプリを活用してみてください。
スタディサプリでは、14日間の無料体験を受けることができます。
まずは無料体験受講をしてみましょう！
⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓
スタディサプリ小・中学講座
スタディサプリ高校講座
数スタの公式LINEを開設しました！