今回は中1数学で学習する「平面図形」の単元から
「角の二等分線の書き方、使える問題は?」
についてイチから解説していきます。
角の二等分線とは、
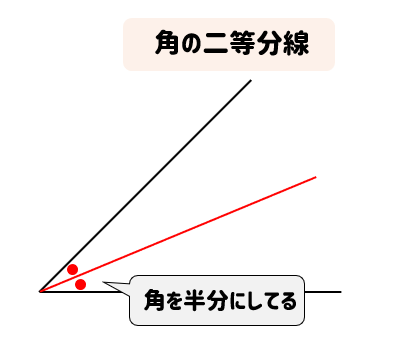
このように、角を二等分している線のことをいいます。
角の二等分線の手順をまとめておくとこんな感じ!

- 角の頂点にコンパスの針をおき、2辺と交わるように円をかく。
- ①の円と辺が交わった点にコンパスの針をおき、同じ大きさの円をそれぞれかく。
- ②の円が交わった点と角の頂点を線で結ぶ。
- 角の二等分線の完成!
書き方はとっても簡単だね(^^)
だけど…どんな問題で使えばいいんだろう…
と悩んでしまう人も多いのでは?
ということで、今回の記事では
角の二等分線がどんな場面で活用できるか
についてもまとめておくので参考にしてくださいね!
記事の最後には「基本作図の活用3選」ということで、模試、入試といった総合力を問われるテストに出てくるような演習課題も用意しています。
角の二等分線のやり方について理解できた方は合わせて活用してみてください^^
角の二等分線の書き方と特徴
では、角の二等分線の書き方を手順に従って確認しておきましょう。
角の二等分線の書き方手順
まずは二等分したい角がある頂点にコンパスの針をおき、2辺と交わるように円をかきます。
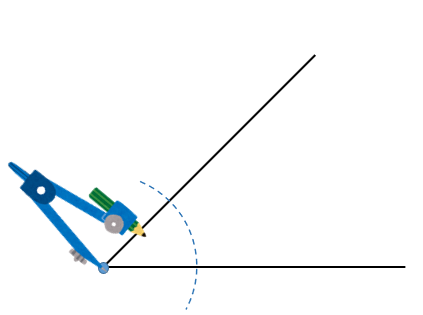
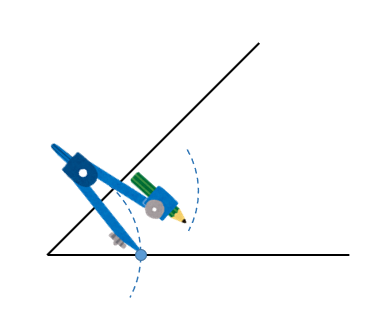
次に、先ほどの円と2辺が交わった点にコンパスの針をおき、
同じ大きさの円を2つかきます。
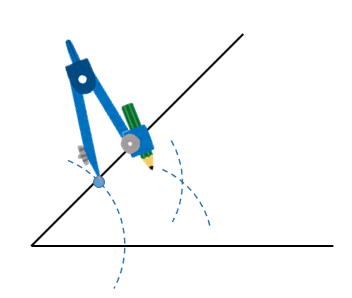
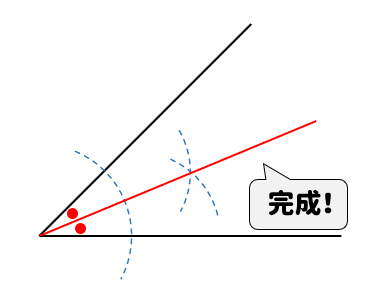
最後に、先ほどの2円が交わる点と角の頂点を線で結んだら
角の二等分線の完成です!
角の二等分線の特徴
角の二等分線とは、その名の通り
角を半分にしている線のことですが、
これ以外にも覚えておきたい特徴があります。
それがコレ!
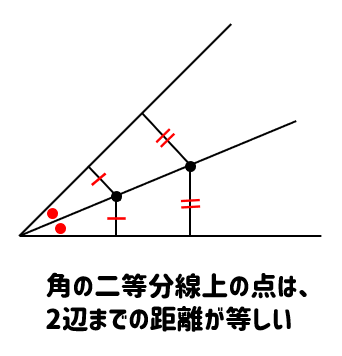
角の二等分線上の点は、どこをとっても
角の2辺からの距離が等しくなっているという特徴があります。
このことを利用した作図問題が多いので、しっかりと覚えておきましょう!
- 角を半分にしている。
- 角の二等分線上の点は、角の2辺からの距離が等しい。
角の二等分線を活用する問題パターン
角の二等分線は様々な問題で活用されます。
角を二等分せよ!
と、直接言ってくれたら分かりやすいのですが
実際の問題では遠回しに問われたりします…
ということで、
ここの章では角の二等分線を活用する問題についてパターン別にみておきましょう。
〇辺からの距離が等しい
【問題】
3辺AB、BC、ACから等しい距離にある点を作図しなさい。
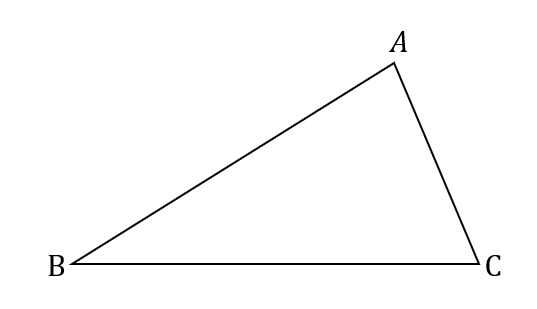
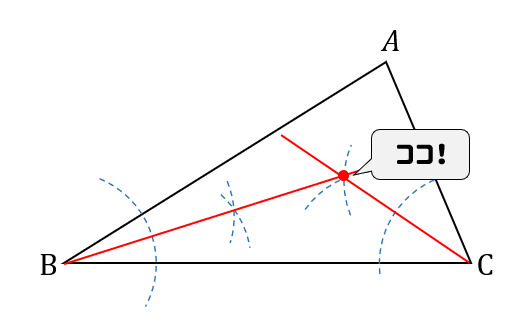
角の二等分線上は、2辺からの距離が等しくなる。
という特徴がありましたね!
〇辺から等しい距離に…
ときたら、角の二等分線を使うようにしてください。
詳しくはこちらの記事でも解説しています。

角の作図
〇°の作図をせよ。
という場合には、角の二等分線が活躍します。
30°を作図する場合には、
60°の角を二等分する。
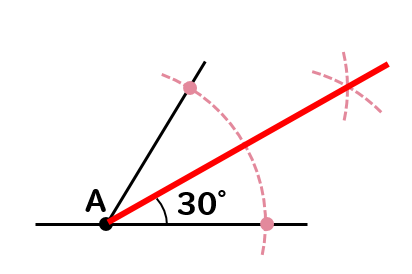
30°の角をさらに二等分すれば、
今度は15°を作図することもできます。

90°の角を二等分すれば、45°も作れますね。
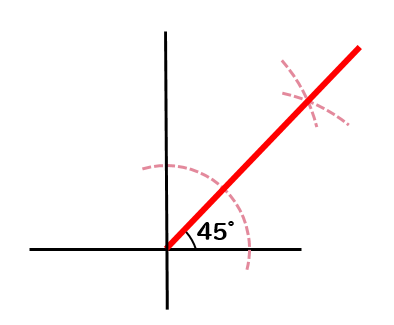
このように、いろんな角度を作図するために
角の二等分線は必須となります。
詳しくはこちらの記事でまとめているので参考にしてみてください、
>【作図】角度15°・30°・45°・60°・75°・90°・105°の作り方を解説!
テストはイジワル…!基本作図の活用3選
さて、ここまでのところで角の二等分線の活用について理解してもらえたと思います^^
ですが、
「よっしゃ、これでテストはバッチリだ!!」
と考えるのはちょっと早いんですね…(^^;)
というのも、テストになると「垂直二等分線」「角の二等分線」「垂線」
これら3つの基本作図を組み合わせた問題が出題されるようになるからです。
つまり、問題を読んだときに「どの作図を活用すればいいのか」「どの順番で作図していけばいいのか」といったことを瞬時に判断できるようにしておかないといけないんですね…
というわけで!
模試や入試によく出てくる基本作図を組み合わせた問題を用意しました(‘ω’)ノ
これを演習することで基本作図は100%の理解に到達できると思うので、テストを受ける前に必ず取り組んでおいてください!
□ たった3題で作図知識を入試レベルにアップさせる演習課題
□ 丸暗記ではない、問題文から導く作図の発想力を伝授!
□ 中1でも入試が解けちゃう!作図が武器になる基本活用術
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れます。
手を動かして作図を体験することで「テストでできる!」を実感することができますよ^^
こちらから今すぐチャレンジしてみよう!
まとめ!
角の二等分線については以上!
まずは書き方の手順を覚えること。
そして、たくさんの問題に触れながら
どんなパターンにおいて活用していけばいいのかを頭に入れておきましょう。
















コメントを残す