【中1作図】最短距離にするためにはどこを通る？？

今回の記事では、中1で学習する作図の単元から

「最短距離の作図」

について解説していきます。

最短距離の作図とは、次のようなやつだね！

【作図問題】

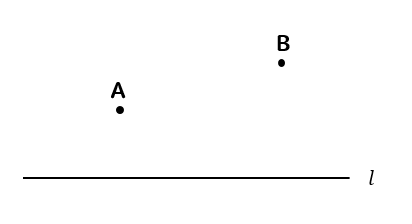
直線\(l\)上にあり、\(AP+PB\)の長さが最小となるような点\(P\)を作図しなさい。

【中1作図】最短距離にするためには？作図手順を解説！

まずは点Aから直線\(l\)に対して、垂線を引きます。

点Aにコンパスの針を置き、直線\(l\)と交わる大きさの円を書きます。

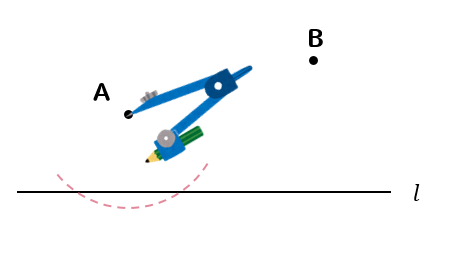
その円と直線\(l\)が交わった2点にコンパスの針を置き、先ほどと同じ大きさの円を2つ書きます。

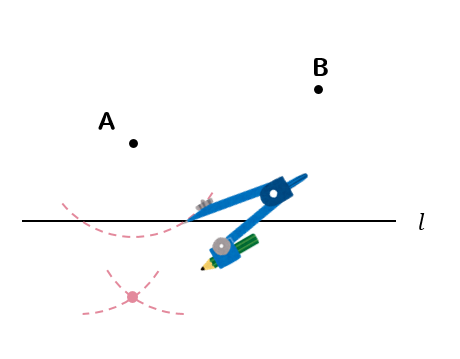
この2円が交わるところを点A’とし、点Aと線で結びます。

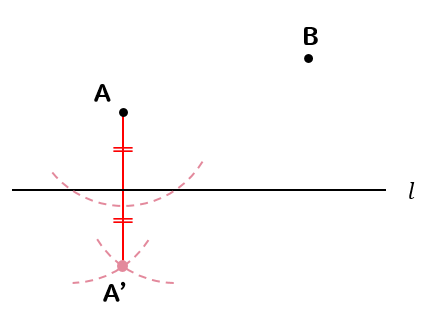
すると、このような線が引けます。

次に、この点A’と点Bを線で結びます。

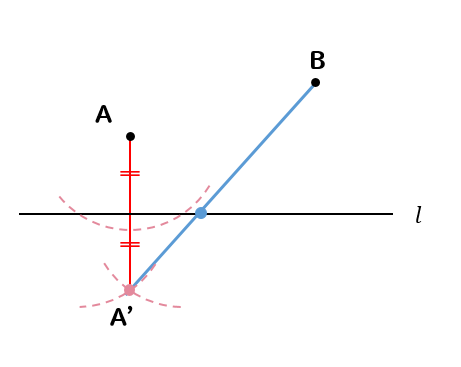
このとき、A’Bと直線\(l\)が交わるところに点を取ります。

すると、この点が…

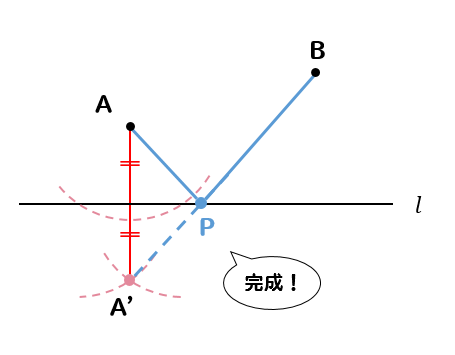
最短距離になる点なのだ！！

ということで作図完成です。

【中1作図】なぜ最短距離になるのか？

それでは、最短距離の作図手順は上で紹介した通りです。

そんなに難しい作業はありませんでしたね(^^)

だけど、なんでこのやり方で最短となる場所を見つけることができるのか…

それについては疑問が残るところです。

ということで、この理由について触れていきます。

折り返した直線の大きさ…と言われても

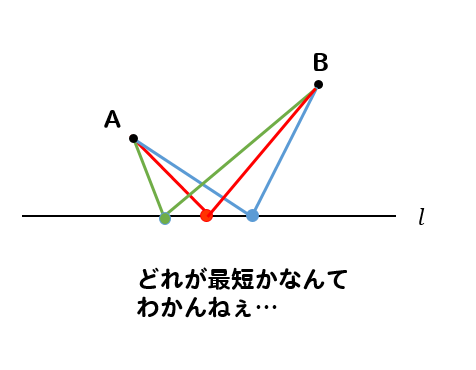
どれが最短になるのかなんて視覚的には分かりにくい。

なので、直線\(l\)に対して点Aと対称にあるところに点A’を取る。

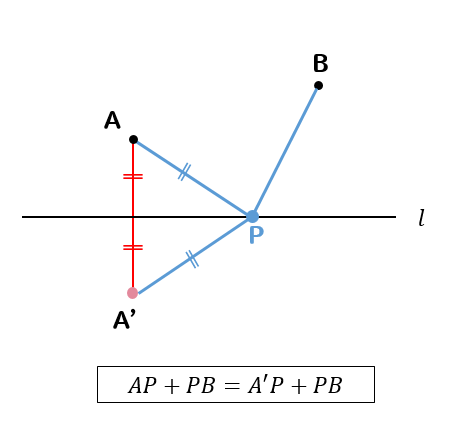
すると、このように

$$AP+PB=A’P+PB$$

という関係になっていることに気が付ける。

ってことは…

\(AP+PB\) の最短を探すのは難しいから

同じ長さである \(A’P+PB\) の最短を探そう！

という発想になります。

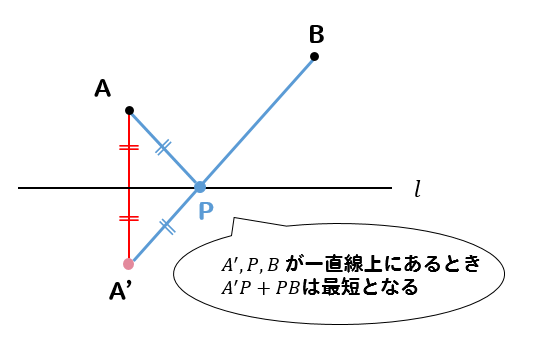
すると、A’、P、Bが一直線上になるとき

\(A’P+PB\) は最短になるではないか！！

つまり、このとき\(AP+PB\) も最短だぞ！

ってな感じで考えていくことができるのです。

【中1作図】最短距離まとめ！

お疲れ様でした！

最短距離を作図するという発想は、初見ではちょっと難しい…

でも、1度解いたことのある人にとっては楽勝なはずだよ(^^)

なので、今回の記事で学んだことはしっかりと頭に入れておいてくださいね。

今回の問題以外にも、ちょっと形が変わって

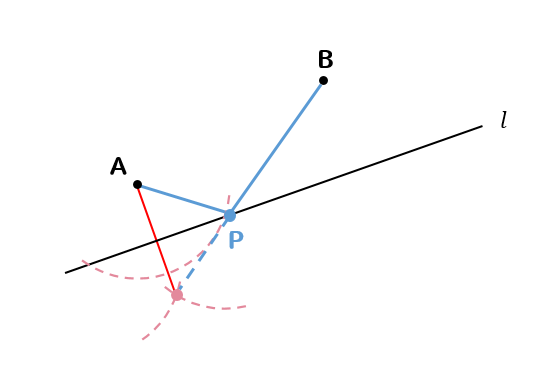
直線\(l\)が斜めになっていたり

誰かが川に水を汲んで、家に届ける

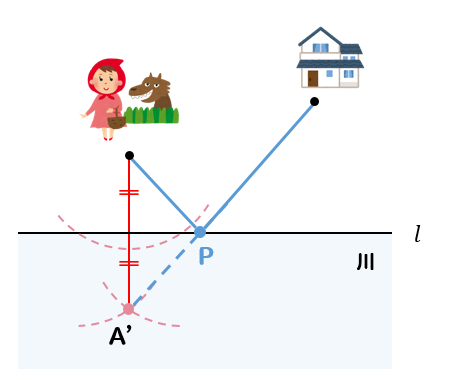
というように場面設定されることもあるけど

基本的にはやり方は同じ！

慌てず基本通りに作図していってくださいね(^^)